今天第二十天表示三十天挑戰過了三分之二，而要學的 LeetCode 演算法或是資料結構的知識也會逐步深入，SwiftUI 套入 App 的應用也會越來越多元，而本次主題是要了解 Tree 是什麼？以及常見討論的 DFS 跟 BFS 是怎麼進行，這系列在 LeetCode 也是不容小看，這個連結整理了 LeetCode Tree 所有的題目，我們可以看到總共有三百多題，表示也是面試常見題型。

Tree 介紹

我們直接切入重點，Tree 雖然分為很多種，但是以 LeetCode 來說，最常見的就是二元樹與二元搜尋樹了，所以資料結構會如下呈現。圖片來源自維基百科。一個節點會記錄自己的值和左右兩個節點，層層往下連接。

class TreeNode<T> {
    var value: T
    var left: TreeNode?
    var right: TreeNode?
    
    init(_ value: T) {
        self.value = value
        self.left = nil
        self.right = nil
    }
}

Swift 程式碼的節點就會長上面那個樣子，value 是該節點存放的值，left 我們稱為左子樹，right 稱為右子樹，當左右節點如果為空，表示我們接觸到這個樹的最底端。

二元搜尋樹 BST (Binary Search Tree)

而二元搜尋樹跟一般的二元樹條件又嚴苛了一點，其節點的排序條件為：對於任意節點，其左子樹中的所有節點的值都小於該節點的值，而其右子樹中的所有節點的值都大於該節點的值。這種特性使得在 BST 中進行搜尋、插入和刪除等操作的平均時間複雜度為 O(log n)。

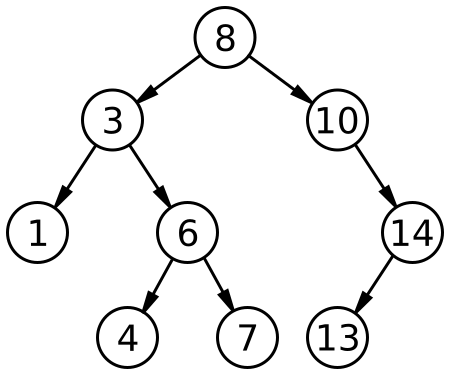
我們可以看到根節點為 8，它左邊的子樹每一個節點都不大於它，右邊的節點全部都大於它，而看節點 3 的左右子樹也符合這個條件，它就是標準的二元搜尋樹。圖片來源自維基百科。

二元樹搜尋方式

在搜尋的方式中，二元樹分為兩種搜尋方式：

1. 深度優先搜尋 DFS (Depth-First-Search)
2. 廣度優先搜尋 BFS (Breadth-First Search)

   1
  / \
 2   3
/ \
4  5

以這個樹為範例，假設要進行深度優先搜尋，那就會優先往這個樹的最深入一直查找，找完再退回去查找另外的子樹，一直到整個樹被找完為止。

所以在這個範例二元樹中深度優先搜尋 DFS 的結果會是：1 -> 2 -> 4 -> 5 -> 3

那如果廣度優先搜尋的話，表示並不會走到最深處，而是走滿樹的該層後再往下進行，所以 BFS 的結果會是：1 -> 2 -> 3 -> 4 -> 5，通常會使用一個佇列來幫助記錄待訪問的節點。

深度優先搜尋三種方式

深度優先搜尋有三種方式，它們搜尋時的順序不一樣。

1. 前序搜尋法，表示中間節點先搜尋 (中左右)，根節點 -> 左子樹 -> 右子樹，以上面的範例樹為案例結果會是：1→2→4→5→3
2. 中序搜尋法，表示中間節點放在中間搜尋 (左中右)，左子樹 -> 根節點 -> 右子樹，以上面的範例樹為案例結果會是：4→2→5→1→3
3. 後序搜尋法，表示中間節點放在後面搜尋 (左右中)，左子樹 -> 右子樹 -> 根節點，以上面的範例樹為案例結果會是：4→5→2→3→1

// 前序搜尋法
func dfs(node: TreeNode?) {
    guard let node = node else { return }
    
    print(node.value, terminator: " ")
    
    dfs(node: node.left)
    dfs(node: node.right)
}

// 中序搜尋法
func dfs(node: TreeNode?) {
    guard let node = node else { return }

    dfs(node: node.left)

    print(node.value, terminator: " ")

    dfs(node: node.right)
}

// 後序搜尋法
func dfs(node: TreeNode?) {
    guard let node = node else { return }

    dfs(node: node.left)
    dfs(node: node.right)

    print(node.value, terminator: " ")
}

廣度優先搜尋 BFS 則利用 queue 來走訪，程式碼就會如下：

func bfs(node: TreeNode?) {
    guard let node = node else { return }
    
    var queue: [TreeNode] = []
    queue.append(node)
    
    while !queue.isEmpty {
        let currentNode = queue.removeFirst()
        print(currentNode.value, terminator: " ")
        
        if let left = currentNode.left {
            queue.append(left)
        }
        
        if let right = currentNode.right {
            queue.append(right)
        }
    }
}

print("\nBFS:")
bfs(node: root) // 輸出: 1 2 3 4 5

LeetCode 題目

找一題 LeetCode 題來學習，本次挑選 1038. Binary Search Tree to Greater Sum Tree，題目是要我們顯示從最右邊的節點一路往上加總結果，並在加總的過程中存放每一個節點，圖片結果如下：

而這題比較特別，走訪順序會是 右→ 中→左，Swift 程式碼如下。

class Solution {
    var sum = 0
    
    func bstToGst(_ root: TreeNode?) -> TreeNode? {
        traversal(root)
        return root
    }

    func traversal(_ root: TreeNode?) {
        guard let node = root else { return }
        
        traversal(node.right)
        sum += node.val
        node.val = sum
        traversal(node.left)
    }
}

時間複雜度為：O(n) 因為我們會走訪所有的節點。

空間複雜度為：O(h) 並沒有另外建立空間給它，但是在遞迴的機制中(遞迴用堆疊的方式)有消耗樹的高度空間。

總結

本次我們清晰理解了 Tree 的資料結構以及它會進行的演算法，隨著學習 LeetCode 題目以及 SwiftUI 交互的過程中，不知不覺已經建立起自己腦中的知識資料庫，這個 SwiftUI 的 App 構建也就越來越完整，也希望在閱讀的你也有一樣的感受。那麼這個系列就值得了。