67. Add Binary

解題程式碼

var addBinary = function (a, b) {
  let carry = 0;
  let result = '';
  const reverseA = a.split('').reverse().join('');
  const reverseB = b.split('').reverse().join('');
  const lognestLength = Math.max(reverseA.length, reverseB.length);

  for (let i = 0; i < lognestLength; i++) {
    let gigitA = i < reverseA.length ? +reverseA[i] : 0;
    let gigitB = i < reverseB.length ? +reverseB[i] : 0;

    let total = gigitA + gigitB + carry;
    result = '' + (total % 2) + result;
    carry = Math.floor(total / 2);
  }
  return carry ? carry + result : result;
};

解題思路、演算法

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料

287. Find the Duplicate Number

解題程式碼

var findDuplicate = function (nums) {
  let slow = 0;
  let fast = 0;

  // 找到環上相遇的點
  while (true) {
    // ex: [1,3,4,2,2]
    // slow = 1, fast = 1, fast = 3
    // slow = 3, fast = 2, fast = 4
    // slow = 2, fast = 2, fast = 4
    // slow = 4, fast = 2, fast = 4, break
    slow = nums[slow];
    fast = nums[nums[fast]];
    if (slow === fast) break;
  }

  // 找到環上的起始點
  let slow2 = 0;
  while (true) {
    // ex: [1,3,4,2,2]
    // slow = 2, slow2 = 1
    // slow = 4, slow2 = 3
    // slow = 2, slow2 = 2
    slow = nums[slow];
    slow2 = nums[slow2];
    if (slow === slow2) {
      return slow;
    }
  }
};

解題思路、演算法

這題本來想用這個解法: 宣告一個長度 n + 1 的陣列 countCharArr，陣列內每個元素預設 0，然後掃過一次 input 陣列，每掃一個數字，就將 countCharArr 對應索引的值加一，例如掃過 nums = [1,3,4,2,2] 後，countCharArr 就為 [0,1,2,1,1]，裡面 index = 2 是因為 2 出現在 input 陣列兩次，所以可以得出 2 重複，但這樣時間複雜度不符合題目要求。

因此使用 Floyd 判圈算法，又稱龜兔賽跑算法(Tortoise and Hare Algorithm) 來解題。

Floyd 判圈算法(Floyd Cycle Detection Algorithm)，又稱龜兔賽跑算法(Tortoise and Hare Algorithm)，是一個可以在有限狀態機、迭代函數或者鍊表上判斷是否存在環，求出該環的起點與長度的算法。

陣列的元素值範圍會在 1~n，長度為 n + 1，我們可以將陣列的每個元素都看成一個 linked list 的節點，其值會指向該陣列索引的元素(節點)，例如圖中陣列第一個元素值 1，就指向索引值為 1 的值，不斷按照相同邏輯去遍歷陣列，可以得出一個有環狀的圖形。而那個環狀的起點就是陣列中重複的值，可以發現圖中的 3、4 都指向 2。

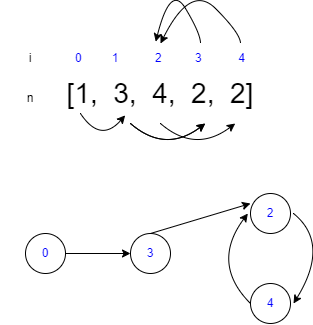
0 作為起點，沒有人指向它，是因為元素值範圍會在 1~n。

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(1)

參考資料

Find the Duplicate Number - Floyd's Cycle Detection - Leetcode 287 - Python

贾考博 LeetCode 287. Find the Duplicate Number

【LeetCode】287. Find the Duplicate Number 解題報告

[LeetCode] 287. Find the Duplicate Number — Linked List — Medium

338. Counting Bits

解題程式碼

var countBits = function (n) {
  let result = [0];
  let minusNum = 1;
  for (let i = 1; i <= n; i++) {
    if (minusNum * 2 === i) minusNum = i;
    result.push(1 + result[i - minusNum]);
  }

  return result;
};

解題思路、演算法

這題實際上是有規律可循的，參考圖片:

從圖片可以發現二進制數字 的最後位數會是 0 1 0 1 不斷循環

並且 0~3, 4~7 的後兩位數也是一個循環(00, 01, 10, 11)

然後到 8 時後三個位數全部歸 0，又是一個循環

所以這題其實可以用動態規劃，出現 1 的次數可以從以下分析看出，也達到題目 Follow up 的條件。

十進制數字   二進制數字    出現 1 的次數
0           0000         0
1           0001         1 = 1 + dp(n - 1)
2           0010         1 = 1 + dp(n - 2)
3           0011         2 = 1 + dp(n - 2)
4           0100         1 = 1 + dp(n - 4)
5           0101         2 = 1 + dp(n - 4)
6           0110         2 = 1 + dp(n - 4)
7           0111         3 = 1 + dp(n - 4)
8           1000         1 = 1 + dp(n - 8)
9           1001         2 = 1 + dp(n - 8)
10          1010         2 = 1 + dp(n - 8)

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料

Counting Bits - Dynamic Programming - Leetcode 338 - Python