今天我們要介紹的是：
logistic regression的起源：
logistic regression的數學式：
logistic regression的程式碼：

• logistic regression的起源與原理：

logistic regression 又稱二元迴歸binary logistic regression，未「binary logistic regression」，名稱雖為迴歸，其實是分類演算法。顧名思義在解決二元分類問題，還有線性迴歸linear regression問題。所謂的二元就是day3我們提的輸入身高體重資訊，讓電腦預測這筆資料到底是男生，還是女生，男生和女生就是二元分類。在數學邏輯上的表示，假設男生為1，女生就是0。以機率來說：男生的機率為p，女生的機率就為1-p。logistic regression的想法就是來自二元機率問題。

• logistic regression 的數學式：

羅吉斯函數logistic function ，又稱sigmoid function，是函數值介於0~1的函數，常見符號為大寫的S，就是取自於函數圖形曲線為S曲線，而來的。

• logistic function : y = \frac{1}{1+e^{-x}}
  logistic function 與 logit function 互為反函數
  logit function :
  x = ln(\frac{y}{1-y})，其中ln表示自然對數，y為男生的機率，1-y為女生的機率
  證明proof：
  ˋˋˋ
  y = \frac{1} {1+e^{-x}|} 「logistic function」
  => y + ye^{-x} = 1
  => e^{-x} = \frac{1-y} {y}，兩邊取ln
  => - x = ln(\frac{1-y} {y}) ，so x = ln(\frac{y}{1-y}) 「logit function」

ˋˋˋ
y =\frac{1} {1+e^{-x}}：
x帶入無窮大為 e^{-x} 為0，y =1
x帶入負無窮大為 e^{-x} 為無窮大，y = 0
所以sigmoid函數就是介於0與1的S曲線
如圖所示，取x在[-7, 7]區間：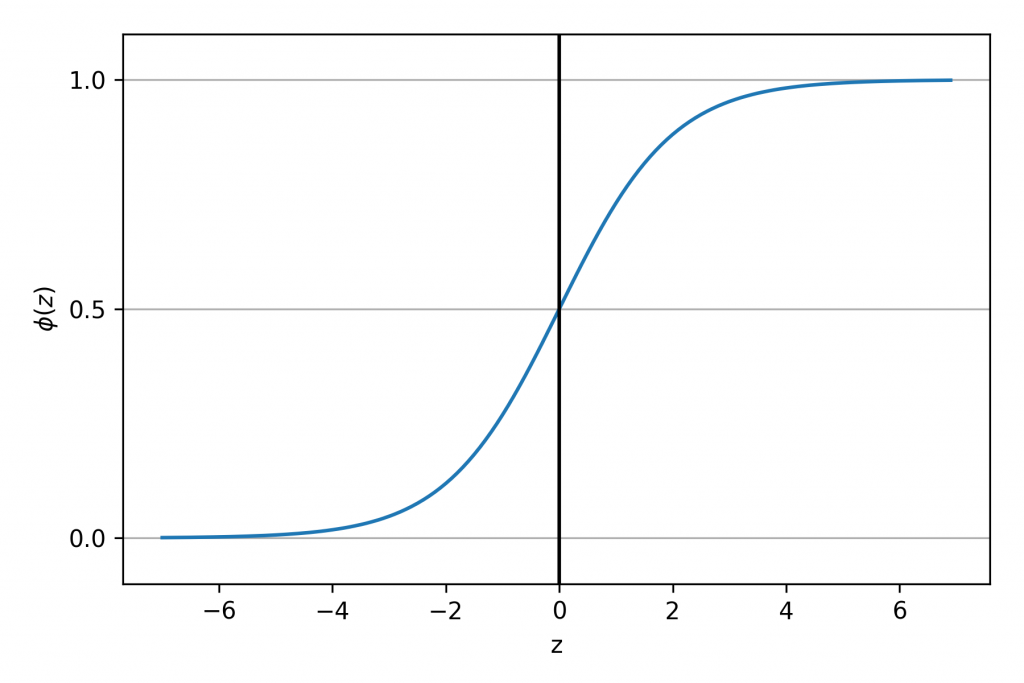

-logistic regression 程式碼範例：

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(C=10, random_state=25, solver='lbfgs'，multi_class='ovr'

lr.fit(X_train, y_train)
lr.predict(X_train)
lr.score(X＿train, y_train)

• C為正規化參數\lambda的倒數，正規化我們以後會再談，先有個概念。

• solver='lbfgs'意思是limited-memory Broyden-Fletcher-Goldfarb-Shanno)「有限
  記憶體BFGS」

• multi_class='ovr'，ovr= one-vs.rest意思是將每一個物件都當作是二元分類處理，

• 明天我們將會談關於K-最近鄰演算法KNN，敬請期待。