• 今天我們要談KNN演算法如下內容：

• KNN演算法起源

• KNN演算法原理

• KNN演算法程式碼

• KNN演算法起源與原理：

世界上所有的事物並非都是二元分類ex.是男是女，或是線性關係ex.吃得越多，體重就會越重，
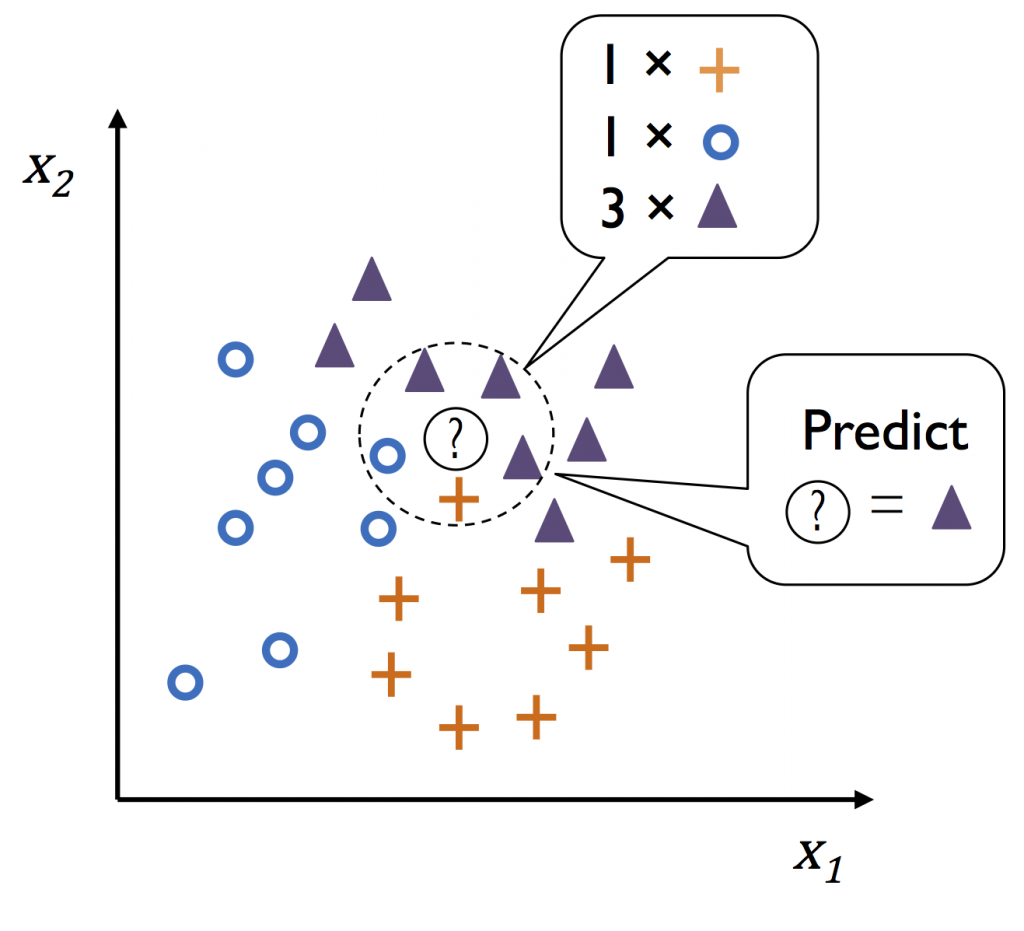
有時候，量化吃的東西與體重的關係，並非成一直線關係，有可能過了某個臨界點，是呈現拋物線曲線上升。這時候，就有KNN演算法的誕生。KNN分類法的概念很簡單，就是先自定一個k值，再取一個歐式距離d，將所有物件繪於圖上，在物件a的d距離內從k個鄰近點找出最多類別多數決majority voting b，而KNN迴歸則是取k個鄰近點的平均值。由下圖我們可以知物件a就是三角形。

• KNN的程式碼：

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=5, metric='minkowski', p=2)
knn.fit(X_train, y_train)
knn.predict(X_train)
knn.score(X_train, y_train)

• 載入sklearn.neighors 套件KNeighborsClassifier。

• n_neighors 就是我們剛才所說的k個最近鄰，這裡取5個最近鄰。

• metric 為度量標準，「minkowski」即是p=1，曼哈頓距離，p=2，歐式距離。這裡取p=2。

• 一般式：d(x^{i}, x^{i}) = \sqrt[p]{\sum_k(|x_k^{i}-x_k^{j}|)^p}，帶入p=1(曼哈頓距離)
  或p=2(歐式距離)。

• 歐式距離（畢氏定理）：圖上兩點距離a(x1, y1)，b(x2, y2) =\sqrt{(x2-x1)^2+(y2-y1)^2}。