這系列結束後,我將繼續挑戰IT鐵人30日:
佛心分享 : it 考照之路
主題:從摸索7個月到下定決心訂下3週後考試:自學取得PMP 3AT 執照
再進入今天的主題前:
我們要先有一個觀念,在二元的線性關係,所謂二元是只有兩個變數x與y,你可以把它想成我們day3所說的特徵與類別(標籤)。對於suvervised learning來說,不管是regression還是classification,我們的目的都是找出一條直線。以regresion:就是找出y = w_0 + w1 \times x的直線,詳細內容,可以回到昨日去看一下,這條直線所代表的意義是x與y兩者關係的趨勢,如下圖所示,在統計上又稱關係,在做數據分析的時候,少不了要運用統計學上的知識,對數據進行預處理,想自學的同學可以google統計學開放式課程,去找適合自己的老師學。因統計不在我們要談的範圍內。對於classification來說:就是要找出一條直線,將物品最佳的分門別類。
線性圖: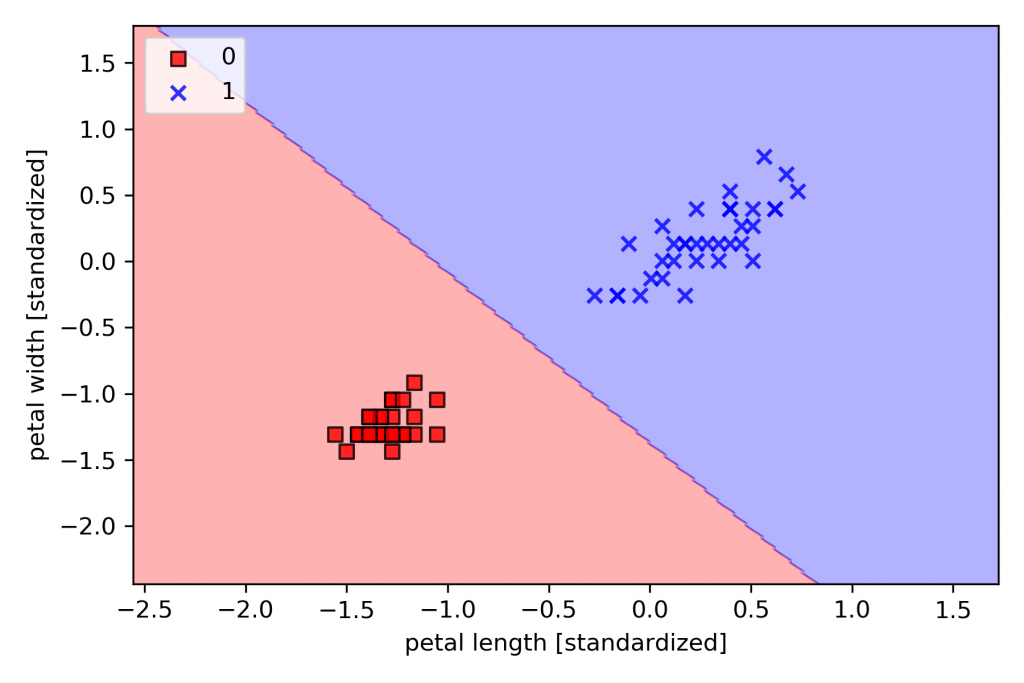
非線性圖: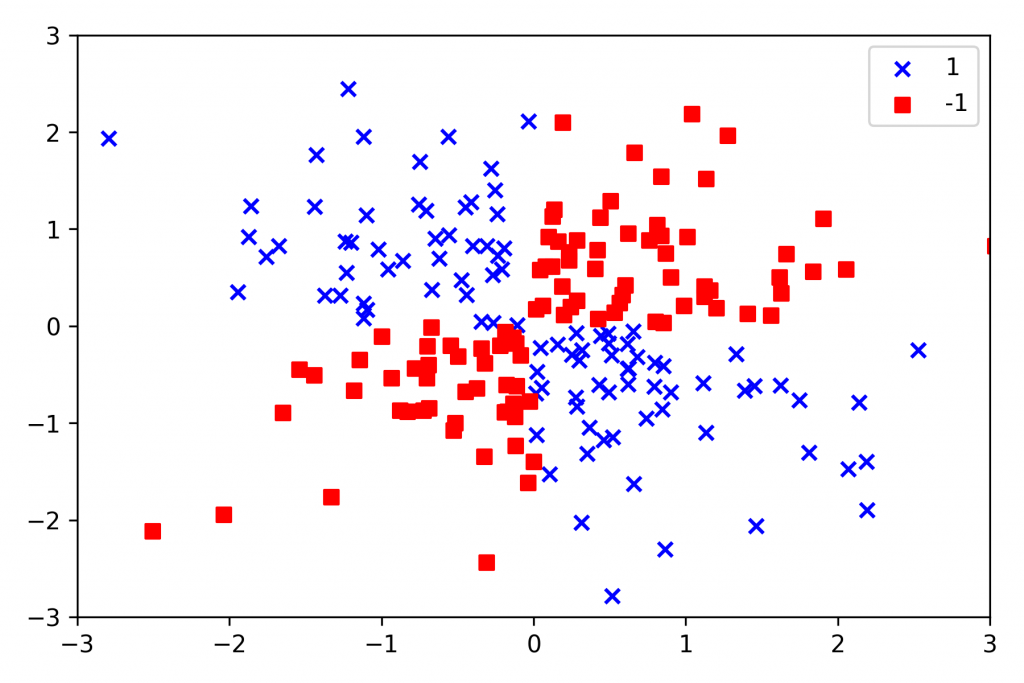
但問題來了,線性關係的問題好解決,但很多時候,我們所遇到的問題,並非是簡單一條線就可以解決的。更多的時候,是屬於非線性關係,如下圖所示,這時候我們可能需要將物件投影到高維(例如:3度空間),利用超平面hyperplane,(未「hyperplane」)在高維度分割,在投影回到二元平面。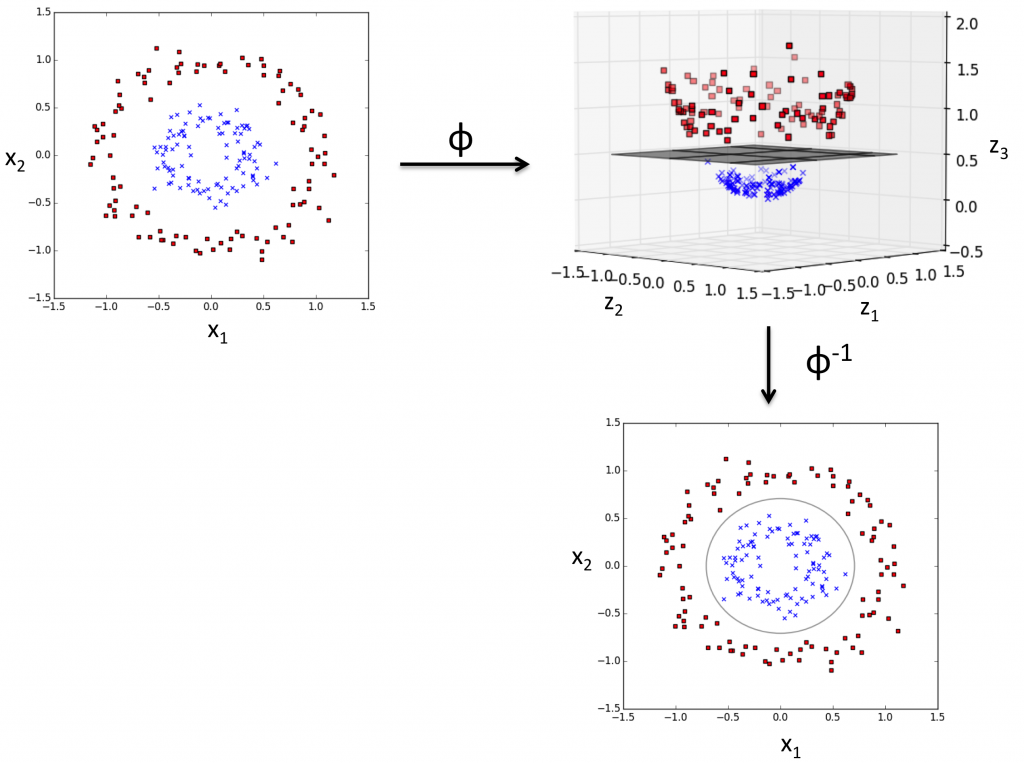
今天我們要談的是:
SVM的起源與原理:
SVM的數學式:
SVM的程式碼:
如同我們上段所提到,很多問題的散佈圖scatter plots是如同上圖所示,並非線性的,而SVM之所在random forest出現以前,廣為大眾所喜愛,就是因爲它同時可以解決線性與非線性問題。
再談數學式之前,先觀察一下上面的圖片,在上圖右邊,我們可已看到有兩類的物件,就是圈圈與叉叉。我們的目標是,在day4有提到SVM的目標函數是「最大化」邊界,也就是希望將這兩類物件分得越開越好。
正超平面postive hyperplane:
w_0 + w^T x_pos = 1 -(1)
負超平面negative hyperplane:
w_0 + w^T x_neg = -1 -(2)
-將上式(1)- (2) 可得:
w^T(x_pos - x_neg) = 2 -(3)
看到上面,同學可能會感到疑惑,為什麼w_0 + w^T x_pos = 1 會是一個平面,昨天 我們明明說只有一個變數x,會是一條直線,在這裏為什麼變成平面?這是因會w^T 是一個矩陣,T表示轉置transpose,表示矩陣行與列互換,矩陣是具有行與列的屬性,是二維的,再加上變數x,所以是一個平面。
將(3) 除以w的長度做正規化,會得到:
\frac{w^T(x_pos-x_neg)} {|| w ||} = \frac{2} { ||w|| }
因objective function 的目標是「最大化」邊界,也就是希望 \frac{2} { || w || }最大,那就是
|| w ||要盡量的小。
w的長度:
|| w || = \sqrt \sum_{i=1}^m w_i^2,\sqrt是開根號,我們所使用的LaTex語法,不熟悉的可以回到day1的標題下去看。
from sklearn.svm import SVC
svm = SVC(kernel='linear', C=10, random_state=18)
svm.fit(X_train, y_train)
svm.predict(X_train)
svm.score(X_train, y_train)
kernel 是核函數:我們選的是線性linear。
C 可以看做是正規化的參數\lambda ,就是要減少誤差項使用。
以上我們介紹的是linear 的svm。
接下來,我們要介紹kernel SVM:
最常使用的「高斯核」Gussian kernel 又稱「徑向基底函數核」Radial Basis Function kernel,RBF kernel。
通式: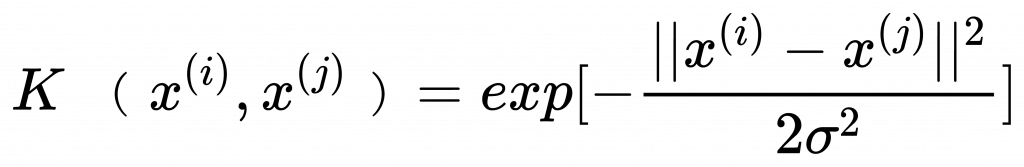
簡化為 :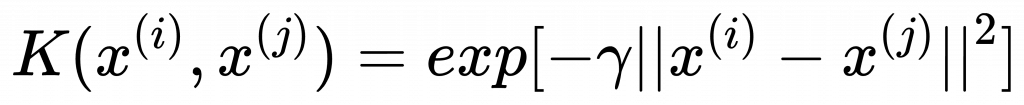
gamma :
\gamma = \frac{1} {2\sigma^2}
from sklearn.svm import SVC
svm = SVC(kernel='rbf', C = 10.0, random_state=25, gamma = 0.10)
# 以下程式碼,因為每個演算法的寫法都大同小異,未「模型配飾,模型預測,模型效能評估」
svm.fit(X_train, y_train)
svm.predict(X_train)
svm.score(X_train, y_train)
exp 是 exponential 是指數的意思,也就是e的幾次方。
gamma 就是上面的 gamma。
未來幾日我們將要談的是:
day18_ML的資料正規化
day19_常見的ML的降維演算法:主成分分析(Principal Component Analysis,PCA)
day20_常見的ML的分群演算法:K-means、 Hierarchy Clustering、DBSCAN
**day21_ML實戰演練 : Kaggle **
day22_監督式學習的效能評估
在這邊要感謝同學的訂閱,讓我每一日一大早都有動力先發文,希望加深的內容也能夠讓用最簡單的方式讓您理解,希望幫助您在非資訊背景的條件下,經由入門介紹,能夠激發您的學習ML的興趣。敬請拭目以待。
