這系列結束後，我將繼續挑戰IT鐵人30日：
佛心分享 ： it 考照之路
主題：從摸索7個月到下定決心訂下3週後考試：自學取得PMP 3AT 執照

-「正規化」在昨日 SVM與 day11 logistic regression出現過，相信同學應該已經對它不陌生，今天我們就要來正式談談ML的正規化：Ｌ1 正規化與Ｌ2正規化。

• 今天我們要談的是：

• 資料存在哪種種類

• 處理資料的過程

• 為什麼要資料正規化

• 資料正規化的種類

• ＭL的正規化：Ｌ1 正規化與Ｌ2正規化。

• Ｌ1 正規化的範例程式碼

• 前言：（資料存在哪種種類）
  自然界的資料，主要依可數或不可數分為兩類：文字與數字，前者如春夏秋冬，後者如身高體重。文字的資料稱為：類別category ; 數字的資料稱為：量化quality。如果你對category這個名詞不熟悉，你就把它解讀為質化quantity。

• 序曲：（處理資料的過程）
  在day2的時候，我們曾經談過資料的「ETL」過程，所謂的「ETL」指的是extract擷取，tansform 轉換，load載入（也稱為晉用），說明在ML之前，都是「髒資料」，我們需要ex.從原始的資料問卷（extract）開始蒐集有效問卷。問卷中的男女（transform）轉換為0與1，再從所有資料取依情況取平均數average，中位數median，最大max，最小min等（load）。還有缺失值要如何處理，這時候要刪除該筆資料，還是用average補等，除了需要依照您本身的domain know或是統計學的知識。總之，資料來之不易，每一筆都是珍貴的資料，任意的刪除一筆，ex.醫療領域疾病的預測，會不會影響整體的研究成果。這部分，不在我們這一系列研究，就交給讀者自行思考。

• 接下來進入主題：（為什麼要資料正規化）
  假如我們現在要研究，人的年紀與收入，是否呈現相關性。首先，人有分男女，如前所述男0女1，年紀則分布到1~117（金氏世界記錄），那收入的分佈就更廣了，若不是將其放在同一把尺上度量，要如何呈現關係。


• 資料正規化的種類：常態化normalization，標準化standardization

• 數學上的常態分佈指的是：極端值佔極少數，中位數(中間)占大多數。

• 我們這裡要談的是「最小-最大尺規」(min-max scaling ) ：

• min-max scaling 公式：

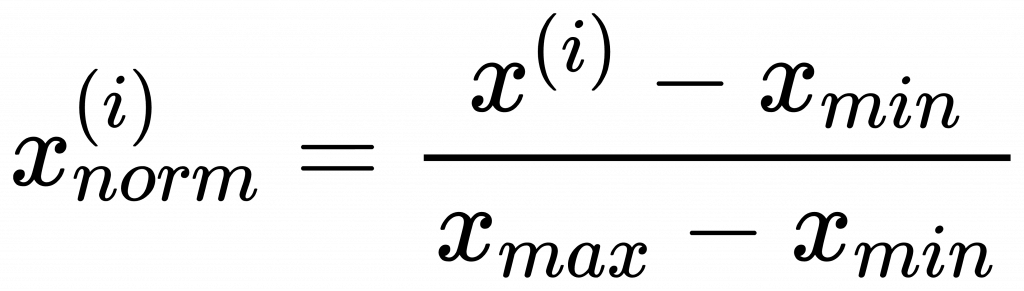
• 它的值介於[0,1] 之間。


• standardization則是與平均值之差，占標準差的比例。標準差的定義在不同的學科有不同的定義。這裡的標 準差是所有資料分別與平均值之差的平方和再除以樣本總數。

• standardization 公式：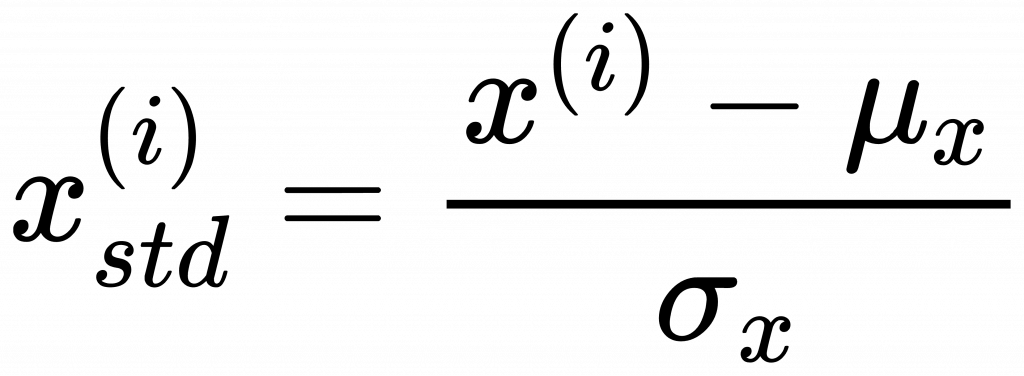
  

• \mu 是所有樣本平均值，\sigma 是所有樣本標準差。這裡的樣本是統計學的術語，就是所有物件全體總數，

• 也是我們在[day3]所談的datasets。

• 標準差公式：

• 

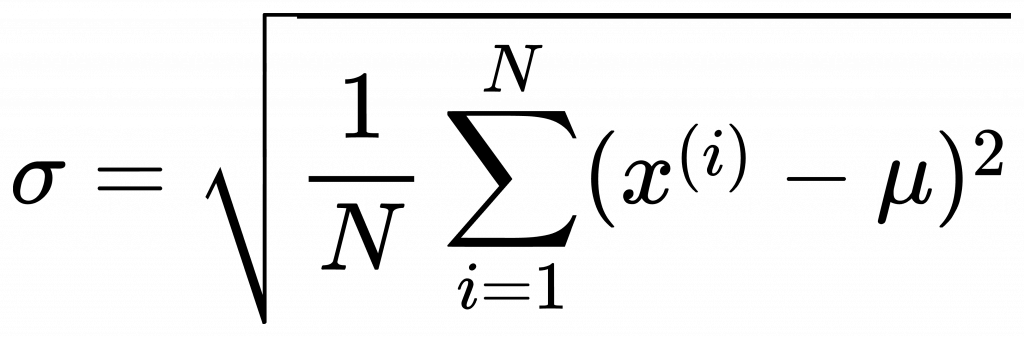
• 同學如果在書上或blog看到normalization或standardization，千萬要仔細看清楚它裡面說的是代表什麼意義，才不會混用。

• 常見ML演算法的正規化：Ｌ1 正規化與Ｌ2正規化。

• L1 正規化的目的：用於減少特徵數，這裡要提醒同學，此處的特徵，是我們[day3]說的特徵，與線性代數中的特徵向量，特徵值是不一樣的，注意不要混用。

• L1 正規化 L1 regularization公式：

• L2 正規化 L2 regularization公式：

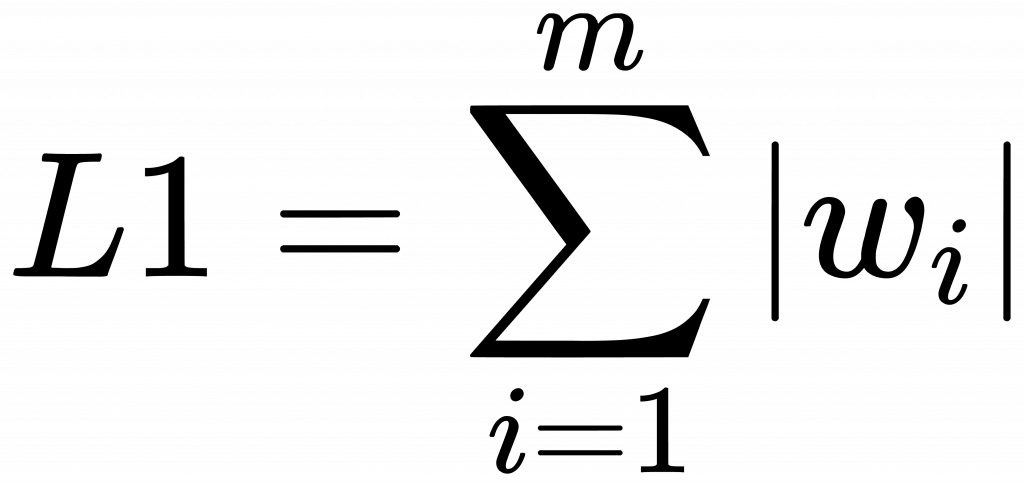
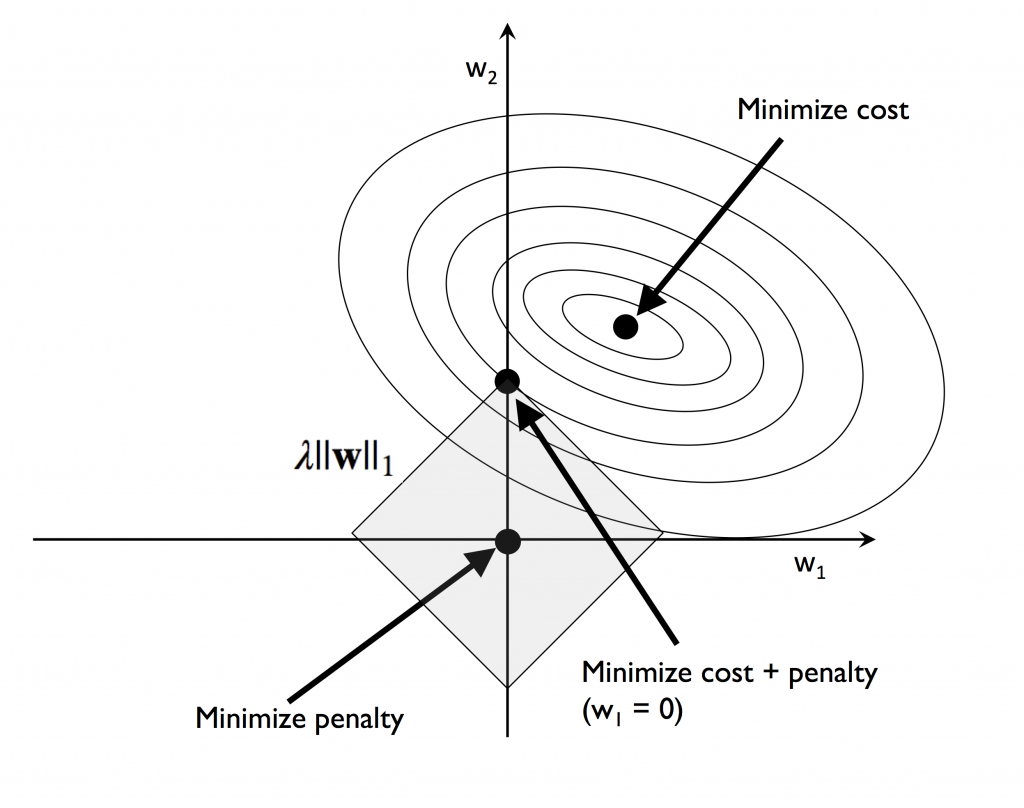
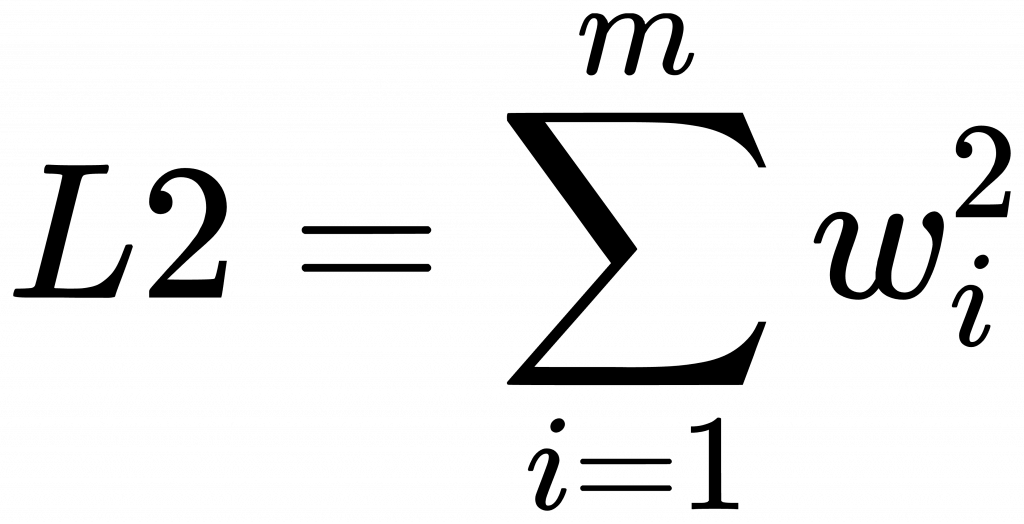
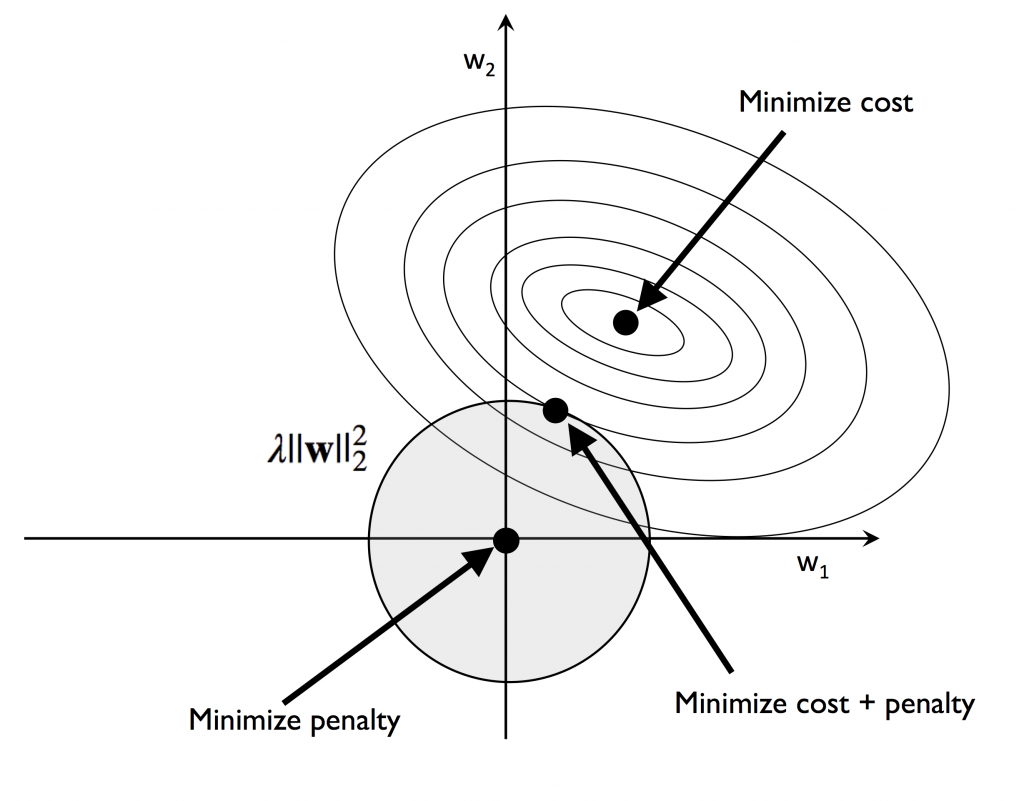
• w 就是[day16] 中所說的 w_0、w_1…等是加權項。你可以把它想成是要調整特徵x大小的媒介。

• 觀察L1與L2的圖型，你注意到了嗎？L1菱型與橢圓型交會處只有一點，而圓型和橢圓型交會處大於一點
  ，這也就說明L1的w項有很多為零，造成許多特徵項都不被採用，所以說是用來減少特徵。

• Ｌ1 正規化的範例程式碼：
  這裡我們就舉幾行簡單logistic regression的範例程式：

from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(penalty='l1', solver = 'lbfgs', multi_class='ovr')

• penalty 選擇L1。其它的部分見[day11]。

• 為什麼要說是逞罰項penalty：

• 這個放在心上，先有個概念，以後我們再談。

• 明天我們將要進入unsupervised-learning，談PCA，近請期待。