前面幾天我們做了幾道題,熟悉了一維數列形式的1-D DP題型,在這類問題中狀態是單一的(例如爬樓梯問題的第i階、扒手問題的第i間房...等等)。
接下來,讓我們更進一步來看看類似的二維矩陣遞迴題型,這也是我們第一次遇到2-D以上的動態規劃問題。
本題取自 Leetcode 62. Unique Paths
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 10^9.
Example 1:
Input: m = 3, n = 7
Output: 28
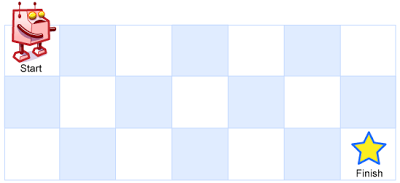
Example 2:
Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
Constraints:
1 <= m, n <= 100
還記得在day4的文章中我們練習過的爬樓梯題目嗎?在該題中,題目規定「要在一步之內走到某一階,只能從前一階或者前兩階」。可觀察到包括這個規則、要從某一個位置走至最終的位置,以及求可能的路徑總數,這些都和本題有共同之處。
本題要求只能向右或者向下走到下一個格子
若我們討論「走到某一格的走法數量」:
狀態:定義paths(i,j)為走至第(i,j)格的路徑數量
轉移式:根據分治法,任何路徑都只能來自左方或者上方一格,因此
paths(i,j) = paths(i-1,j) + paths(i,j-1)
邊界條件:分析題目後可知:
1(注意不是0)因此,若我們計算實際的走法數,會發現在最左一行的任何一格,以及最上一列的任何一格,都僅有一種走法。(就是從出發格直直走)
從矩陣類的問題開始,我們會遇到逐漸複雜化的邊界條件,讀者可以多注意在兩個策略的實作當中如何去處理邊界條件。
母問題所求:求paths(m-1, n-1)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
@cache
def paths(i,j):
if i==0 or j==0: return 1 # 最左or最上一格
return paths(i-1, j) + paths(i, j-1)
return paths(m-1, n-1)
注意:在遞迴過程中,子問題會被重複問到(每一格可以往右或者往下走),因此需要使用@cache或者手刻快取來記錄答案。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 產生一個 m x n 矩陣來記錄。path(i,j)答案 => dp[i][j]
dp = [[0 for _ in range(n)] for _ in range(m)]
# 由上往下、由左往右迭代計算
for i in range(m): # y軸: 0 ~ m-1
for j in range(n): # x軸: 0 ~ n-1
if i == 0 or j == 0: # 最上/最左一格
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
可以發現,當需要紀錄的狀態不只一個(例如本題是一個2-D的DP),則bottom-up我們所規劃的儲存答案陣列,以及計算的順序就會變得比較複雜。
設計計算順序時要注意:後算的問題,會採用先算的問題的答案
以本題來說,我們規劃了一個m x n的矩陣,用來記錄paths(i,j) = dp[i][j],至於計算的順序,則是從上到下計算每一列(for i),並且每一列從左到右計算(for j)。
因為從上到下計算,所以計算時,用到「上面一格」的答案時已經算好了,直接從dp取用即可。同理,因為從左到右計算,所以用到「左邊一格」的答案時已經算好了,直接從dp取用即可。
不過,上面所示範的答案,還有(儲存空間上)優化的空間!
觀察計算順序以及轉移式之後,我們會發現:
換言之,並不需要占用m x n的空間,而只需要保留(目前所計算到的)最後一列的答案。
優化後的bottom-up dp如以下範例:
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [1 for _ in range(n)] # 最上一列:均只有1種路徑
# 由上往下、由左往右迭代計算
for _ in range(1,m): # y軸: 1 ~ m-1
for j in range(1,n): # x軸: 1 ~ n-1
dp[j] = dp[j] + dp[j-1]
return dp[-1]
概念是:只用1-D的List來記錄某一行的答案,並且每計算一格,就直接覆蓋掉其上方一格的答案(因為用不到了)。
轉移式dp[j] = dp[j] + dp[j-1]看起來會覺得有點奇怪,這是因為我們直接挪用上一列的答案陣列,繼續記錄下一列的答案。
等號後面的dp[j]代表的是上面一格的路徑數,而dp[j-1]代表的是左邊一格的路徑數
這個技巧又稱為在原址(inplace)動態規劃,應對空間要求比較刁鑽的題目時,大多都靠這招就可以解決。
時間複雜度 = 狀態轉移數 x 計算複雜度
本題的狀態數 = O(m x n),計算複雜度 = O(1)
因此時間複雜度 = O(m x n)
因為需要記住每題子問題的答案,空間複雜度 = 狀態數 = O(m x n)
如果使用原址的bottom-up,則空間複雜度 = O(n)
本題有數學公式解,其實這個問題也出現在中學的排列組合問題中。排組給出的解法是這樣的:
無論何種路徑,要從(0,0)走到(m-1,n-1),必定需要往下走m-1步,且往右走n-1步。
例如:測資Example2:m = 3, n = 2,必須往下2步且往右1步。則3種走法可以分別寫作:
↓ ↓ →
↓ → ↓
→ ↓ ↓
換言之,原問題等價於求m-1個A物與n-1個B物的線形排列數,即C(m+n-2, m-1)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
return comb(m+n-2, m-1)
當然,公式解只適用於簡單的模板題,一旦題目稍有變化(例如地圖上挖個不能走的洞)便無法使用。
不過這種「OOO問題其實等價於XXX問題」的思維可謂許多演算法問題(或者廣泛的說是數學問題)的突破口,值得我們學習。
本題取自 Leetcode 64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
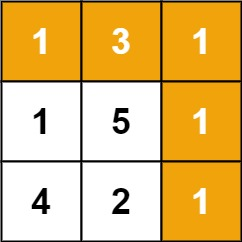
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.
Example 2:
Input: grid = [[1,2,3],[4,5,6]]
Output: 12
Constraints:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200
迷宮的走法和上一題(Leetcode 62.)相同,只能往右或者往下。
上一題要求所有不同的路徑總數,而本題則是在迷宮中填入數字,要求這些路徑之中,該路徑所經過的數字總和最小的。
經過上一題的練習,不難找到這個子問題:
對於迷宮中的某一格grid[i][j],從起點grid[0][0]走到這格,最小數字總和的路徑是多少?
因為走到這格,只能從左邊一格grid[i][j-1]或者上面一格grid[i-1][j]走來,所以只要從這兩格的子問題答案中求較小值,再加上grid[i][j]這格本身的數值,即為子問題的答案。
題目所求則為最右下角那格grid[m-1][n-1]的子問題答案。
狀態:minSum(i,j)
從起點grid[0][0]走到grid[i][j]的路徑中最小數字總和
轉移式:
minSum(i,j) = grid[i][j] + min( minSum(i-1,j), minSum(i,j-1) )
最小問題(邊界條件):
當子問題問到最左一行時,即minSum(i,0),此時不需要考慮「左邊」的minSum(i,-1),因為左邊已經沒有格子了。同理,當子問題問到最上一列的minSum(0,j)時,不需要考慮「上面」的minSum(-1,j),因為上面已經沒有格子了。
可以多觀察在以下的實作中如何處理邊界條件。
題目所求(母問題):minSum(m-1,n-1)
注意:在遞迴過程中,子問題會被重複問到(每一格可以往右或者往下走),因此需要使用@cache或者手刻快取來記錄答案。
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
@cache
def minSum(i,j):
# 出發點
if i==0 and j==0: return grid[0][0]
# 最左一行或者最上一列,往前一格遞迴時
# 透過回答無限大,來讓min自動排除這個路徑
if i==-1 or j==-1: return float('inf')
# 狀態轉移式
return grid[i][j] + min(
minSum(i,j-1) , minSum(i-1,j)
)
# 回答母問題答案 (最右下角那格)
return minSum(len(grid)-1, len(grid[0])-1)
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0]) # 矩陣的高與寬
# 建立記錄答案用的空矩陣
dp = [[0 for _ in range(n)] for _ in range(m)]
# 出發點
dp[0][0] = grid[0][0]
# 最上一列,只能從左邊走來
for j in range(1, n):
dp[0][j] = grid[0][j] + dp[0][j-1]
for i in range(1, m):
# 每列的最左一格,只能從上面走來
dp[i][0] = grid[i][0] + dp[i-1][0]
for j in range(1, n):
# 狀態轉移式
dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
# 返回母問題答案:最右下角那格
return dp[-1][-1]
和前一題類似的做法,若要更加節省空間也可以做inplace的處理:
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
# grid 高、寬
m, n = len(grid), len(grid[0])
# 記錄「已計算過的最後一列」答案用的陣列
## 出發點
dp = [grid[0][0]]
## 最上面一列
for j in range(1, n):
dp.append(grid[0][j] + dp[j-1])
# 由上往下計算每一列
for i in range(1, m):
# 最左邊一格
dp[0] = grid[i][0] + dp[0]
# 由左往右計算每一格
for j in range(1, n):
# 轉移式
dp[j] = grid[i][j] + min(dp[j-1], dp[j])
# 母問題答案(最右下一格)
return dp[-1]
和前一題類似,因為計算子問題答案只需要左邊一格和上面一格,且我們由上至下逐列計算,因此,當計算完某格之後,其上方一格的答案已經不需要了。所以我們只需要反覆用一個1-D的陣列來記錄2-D的「每一行」答案。
這樣做的優點是最省空間,但轉移式「乍看之下」會跟分治法推導的不同,需要注意:
dp[j] = grid[i][j] + min(dp[j-1], dp[j])
dp[j],計算並紀錄子問題答案minSum(i,j)
dp[j-1]是剛計算過的minSum(i,j-1)
dp[j]是還沒被覆蓋掉的「上一行的答案」,所以其實代表的是minSum(i-1,j)
這樣分析之後就能看出,其實和前面分治法所推導的轉移式仍是相同的。
時間複雜度 = 狀態轉移數 x 計算複雜度
本題的狀態數為O(m x n),計算複雜度為O(1),因此總複雜度為O(m x n)
記錄所有子問題答案的空間複雜度為O(m x n)。
若採用 inplace Bottom-Up 的寫法則可以降到O(n)。
本題取自 Leetcode 63. Unique Paths II
You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.
Return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The testcases are generated so that the answer will be less than or equal to 2 * 10^9.
Example 1:
Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Example 2:
Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Constraints:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] is 0 or 1.
同樣作為第一題(Leetcode 62.)的變化題,本題在迷宮加入了障礙物,走迷宮的規則不變(只能往右、下),並且求左上走到右下、不遇到障礙物的路徑總數。
我們仍可以問和第一題相同的子問題:對於某一格,走到該格的總路徑數為多少?
狀態:定義paths(i,j) = 走到第(i,j)格的路徑總數
轉移式:
這格有障礙物:grid[i][j] == 1,則:
paths(i,j) = 0
這格沒有障礙物:grid[i][j] == 0,則:
paths(i,j) = paths(i-1,j) + paths(i,j-1)
邊界條件:和第一題相同:
paths(0, 0):若沒有障礙物則= 1,若有障礙物則= 0
i、j不能 < 0)注意:在遞迴過程中,子問題會被重複問到(每一格可以往右或者往下走),因此需要使用@cache或者手刻快取來記錄答案。
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
@cache
def paths(i,j):
# 有障礙物
if obstacleGrid[i][j]: return 0
# 出發點
if i==0 and j==0: return 1
# 最上一列
if i==0: return paths(i,j-1)
# 最左一行
if j==0: return paths(i-1,j)
# 一般情況
return paths(i,j-1) + paths(i-1,j)
# 回答母問題答案 paths(m-1, n-1)
return paths(len(obstacleGrid)-1, len(obstacleGrid[0])-1)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [[0 for _ in range(n)] for _ in range(m)]
for i in range(m):
for j in range(n):
# 有障礙物
if obstacleGrid[i][j]==1: dp[i][j] = 0
# 無障礙物
## 出發點
elif i==0 and j==0: dp[i][j] = 1
## 最上一列
elif i==0: dp[i][j] = dp[i][j-1]
## 最左一行
elif j==0: dp[i][j] = dp[i-1][j]
## 其他情況
else: dp[i][j] = dp[i-1][j] + dp[i][j-1]
# 回答母問題答案 dp[m-1][n-1]
return dp[-1][-1]
若要更加節省空間也可以做inplace的處理:
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [0 for _ in range(n)]
for i in range(m):
for j in range(n):
# 有障礙物
if obstacleGrid[i][j]: dp[j] = 0
# 無障礙物
## 出發點
elif i==0 and j==0: dp[j] = 1
## 最上一列
elif i==0: dp[j] = dp[j-1]
## 最左一行
elif j==0: pass
## 其他情況
else: dp[j] += dp[j-1]
# 回答最右下角 dp[m-1][n-1]
return dp[-1]
值得一提的是,儘管大部分的矩陣題資料緊密,Bottom-Up通常算得比較快,但本題在障礙物很多的情況下,反而是Top-Down算得比較快。
箇中差異在於,Top-Down的遞迴函式有early return的性質,每當遇到障礙物,直接返回0,並不會繼續往起點遞迴,去問前一格的子問題。
由於Bottom-Up必定計算所有的狀態,當障礙物很多時,Top-Down這種剪枝(pruning)的效果就發揮出來,省掉了很多不必要的計算。
以這題來說,若某格由於前後都被障礙物堵死,沒有任何「合法」的路徑能通過,此時Bottom-Up仍然會遍歷計算每一格,但是Bottom-Up在遇到其中一端的障礙物時就直接early return掉(放棄這條路徑),並不會計算到這一格的狀態。
這也正是大多數圖論的DP問題使用Top-Down策略都能較容易解決的原因。當題目的網絡越複雜,節點的規則、條件判斷越來越多時,Top-Down就能發揮剪枝的優勢;反而Bottom-Up會苦於無法掌握計算順序,或者把資源都拿去計算根本用不到的節點形成無形的浪費。
不過本題只是簡單的有/無障礙物判斷,所以兩個策略的效能表現其實差不多。
時間複雜度 = 狀態轉移數 x 計算複雜度
本題的狀態數為O(m x n),計算複雜度為O(1),因此總複雜度為O(m x n)
記錄所有子問題答案的空間複雜度為O(m x n)。
若採用 inplace Bottom-Up 的寫法則可以降到O(n)。
矩陣題型都大同小異,重點在於掌握合法路徑的規則來推導轉移式。
以上為Day06的內容!感謝你的閱讀,如果有不同的想法或心得,歡迎留言一同討論!
本文也同步登載在我的個人部落格,記錄我的學習筆記與生活點滴,歡迎來逛逛。
明天我們會接著再看幾題矩陣的題型。
