🟨編輯距離

本題取自 Leetcode 72. Edit Distance

題目

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')


Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
 

Constraints:

0 <= word1.length, word2.length <= 500
word1 and word2 consist of lowercase English letters.

分析

本題定義所謂的「編輯距離」edit distance 為：將word1修改為word2所需編輯的總字母數。每次編輯可以插入/刪除/更改一個字母。

給定兩個字串，要求最少的編輯距離。

和day11「最長的共同子序列(LCS)」類似，我們可以用兩個字串各自的index作為狀態，來比較該位置的字母是否相同(是否需要編輯)。

分治法

假設我們目前正在比較word1[i1]和word2[i2]的字母，則會有兩種狀況：相同或不同。

若word1[i1] == word2[i2]：

既然字母相同，就不需修改。繼續比較後一個字母。

這邊有一點貪心算法的概念在裡面。既然題目要求最小的編輯距離，若字母相同卻去編輯，自然就不可能會是最小的。

若word1[i1] != word2[i2]：

字母不同，則根據題目提供的編輯規則，有三種編輯方式，任何一種方式都會增加1的「編輯距離」：

1. 刪除word1[i1]
2. 在這個位置插入word2[i2]
3. 把word1[i1]修改成word2[i2]

三種編輯方式所對應的狀態轉移式如下圖：

設計狀態、找出轉移式與最小問題

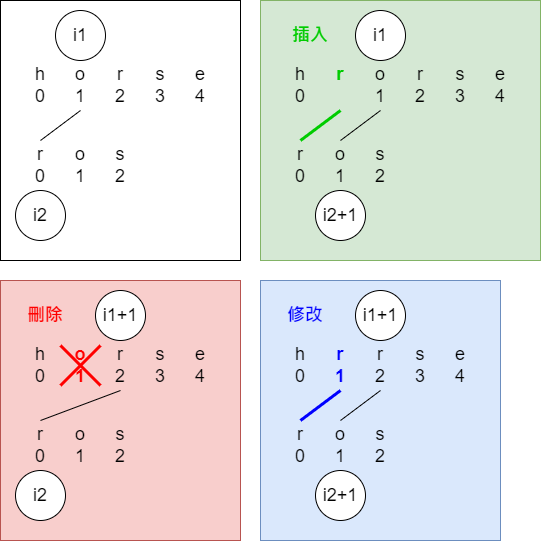
狀態：以dis(i1, i2)來表示正在比較word1[i1]和word2[i2]。

轉移式：

若word1[i1] == word2[i2]：

dis(i1, i2) = dis(i1+1, i2+1)

若word1[i1] != word2[i2]：

dis(i1, i2) = 1 + min(dis(i1+1, i2+1), dis(i1, i2+1), dis(i1+1, i2))

邊界條件(最小問題)：

當i1 == len(word1)，代表word1的所有字母都已經編輯完畢，但是word2還有剩下的字母，代表需要新增word2剩餘的所有字母，dis(i1, i2) = len(word2)-i2

當i2 == len(word2)，代表word2的所有字母都已經對應完畢，但是word1還有剩下的字母，代表需要刪除word1剩餘的所有字母，dis(i1, i2) = len(word1)-i1

母問題(題目所求)：dis(0, 0)

實作

Top-Down DP

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        @cache
        def distance(i1, i2):
            if i1 == len(word1):
                return len(word2) - i2
            if i2 == len(word2):
                return len(word1) - i1
            if word1[i1]==word2[i2]:
                return distance(i1+1,i2+1)
            return 1 + min(distance(i1+1, i2), distance(i1, i2+1), distance(i1+1,i2+1))
        return distance(0,0)

Bottom-Up DP

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [[0]*(len(word1)+1) for _ in range((len(word2)+1))]
        for i2 in reversed(range(len(word2)+1)):
            for i1 in reversed(range(len(word1)+1)):
                if i1 == len(word1):
                    dp[i2][i1] = len(word2) - i2
                elif i2 == len(word2):
                    dp[i2][i1] = len(word1) - i1
                elif word1[i1] == word2[i2]:
                    dp[i2][i1] = dp[i2+1][i1+1]
                else:
                    dp[i2][i1] = 1 + min(dp[i2+1][i1], dp[i2][i1+1], dp[i2+1][i1+1])
        return dp[0][0]

和前面在矩陣題型一樣，為了處理index overflow又不讓轉移式變得複雜化，狀態增加了最右邊一行和最左邊一列作為邊界條件。

當然也可以使用Rolling或者Inplace的技巧來節省空間，例如下例為Rolling，只保留前一列的答案。

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp = [0]*(len(word1)+1)
        for i2 in reversed(range(len(word2)+1)):
            dp2 = [0]*(len(word1)+1)
            for i1 in reversed(range(len(word1)+1)):
                if i1 == len(word1):
                    dp2[i1] = len(word2) - i2
                elif i2 == len(word2):
                    dp2[i1] = len(word1) - i1
                elif word1[i1] == word2[i2]:
                    dp2[i1] = dp[i1+1]
                else:
                    dp2[i1] = 1 + min(dp[i1], dp2[i1+1], dp[i1+1])
            dp = dp2
        return dp[0]

以上兩例為了使用和top-down相同的轉移式，所以是從字尾算回字首(for ... in reversed(range...))。當然，也可以重新規劃轉移式，從字首開始算。

broad first search(BFS)

從bottom-up記錄答案矩陣的角度來看，狀態轉移式可以整理如下：

我們的目標是從左上角走到右下角(比對所有的字母)，並且找出edit distance最小的路徑。

如果善用這層思維，我們就可以用另一種視點切入這個問題：

先從左上角走出「0步」(edit distance == 0)，看0步能夠走到哪些點。接著就走1步，一樣紀錄能夠走到的點...依此類推，直到我們走到了右下角(i1==len(word1) and i2==len(word2))，此時，當下的edit distance就必定是最小的。

若讀者熟悉基本演算法，就會發現這其實就是broad first search(BFS，廣度優先搜尋)演算法的邏輯。

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        toGo = [(0,0)]
        visited = set()
        distance = 0
        while True:
            nextToGo = []
            while toGo:
                i1, i2 = toGo.pop()
                if (i1, i2) in visited: continue
                visited.add((i1,i2))
                if i1 == len(word1) and i2 == len(word2):
                    return distance
                if i1 == len(word1):
                    nextToGo.append((i1,i2+1))
                elif i2 == len(word2):
                    nextToGo.append((i1+1,i2))
                elif word1[i1] == word2[i2]:
                    toGo.append((i1+1,i2+1))
                else:
                    nextToGo.extend([(i1,i2+1),(i1+1,i2),(i1+1,i2+1)])

            distance += 1
            toGo = nextToGo

計算至最終答案的邏輯可以參考下圖：

注意到一個細節：

由於我們是從低的distance開始計算，外層的while迴圈每層會讓distance+1，因此使用visited這個Set來記錄已經走過的點，如果已經走過就不再重複計算，因為第二次算的distance絕對不會更低。

這點和動態規劃「不去計算重複的狀態」的概念類似，但要注意的是，三者的計算順序不同。

• 在Bottom-up動態規劃演算法中，我們多半是沿著陣列或者矩陣的順序，也就是狀態index的順序來計算答案。
• 而在Top-down動態規劃演算法中，遞迴函式多半是照著類似DFS(depth first search)演算法的順序進行計算。
• 在本例示範的BFS演算法，則是每次都計算「相鄰的一步」範圍內的狀態，直到找到目標(終點)之後，無論有沒有剩餘未計算的狀態都直接終止計算。

因此，並不是所有的動態規劃題都適合改寫成BFS，本例由於要找「最短」路徑，且我們恰能照著路徑長短的順序計算，恰可以改寫成BFS的邏輯。

複雜度分析

時間複雜度

時間複雜度 = 狀態轉移數 x 計算複雜度

本題的狀態數 = O(n x m)，n、m分別為word1、word2的長度

計算複雜度為O(1)

因此總時間複雜度 = O(n x m)

值得一提的是，本題的時間最佳解會是BFS。儘管時間複雜度也是接近O(n x m)，但由於BFS不需要計算所有的狀態，在冗餘狀態很多時就會比DP來得快。

空間複雜度

空間複雜度 ＝ 狀態數 ＝ O(n x m)

若採用Rolling Bottom Up DP的技巧，則降低一個維度，空間複雜度 ＝ O(n)

結語

本題我們從與LCS的比對邏輯類似的角度出發，發展出了DP的算法。此外也透過bottom-up DP的記錄答案矩陣的抽象化找到另一個殊途同歸的作法：BFS。

從本題我們亦發現，倘若轉移式可以抽象化為矩陣當中的路徑，且所求為最短路徑時，往往BFS可以獲得比DP更佳的時間效能。

以上為Day13的內容！感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！

本文也同步登載在我的個人部落格，記錄我的學習筆記與生活點滴，歡迎來逛逛。

明天會繼續看不同的字串題型。