今天我們來看一個字串類的經典題型:最長回文子字串(LPS)
本題取自 Leetcode 5. Longest Palindromic Substring
Given a string s, return the longest
palindromic substring in s.
A string is palindromic if it reads the same forward and backward.
A substring is a contiguous non-empty sequence of characters within a string.
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.
Example 2:
Input: s = "cbbd"
Output: "bb"
Constraints:
1 <= s.length <= 1000
s consist of only digits and English letters.
根據題意,回文字指的是正著讀、倒著讀都一樣的文字(字數不限奇數偶數,因此abba、aba、aa、a都是回文字)
子字串指的是從給定字串中切一段連續的字母下來形成的字串。
本題要從給定的字串的「屬於回文字的子字串」當中找出「最長的」。
乍看之下,可能會不知道從何著手,遇到這種題目時,可以試著從暴力法開始,再想想如何優化。
遍歷剪出所有的子字串,並且依序檢查他們是否為回文字,若是則紀錄其中最長的。如下例:
class Solution:
def longestPalindrome(self, s: str) -> str:
# 紀錄最長的回文子字串
LPS = ''
# 遍歷所有可能的子字串
for i in range(len(s)):
for j in range(i+1,len(s)+1):
# sub: 子字串
sub = s[i:j]
# 若sub為回文字且比上一個長,則更新為最長的回文子字串
if sub == sub[::-1] and len(sub)>len(LPS):
LPS = sub
return LPS
時間複雜度 = 子字串數 x 判斷是否為回文數的計算複雜度
本題的子字串數 = O(n^2),判斷是否為回文數的計算複雜度 = O(n),因此總複雜度 = O(n^3)
顯然這並不夠好。因此要接著思考,如何降低時間複雜度。
在暴力法的過程中,我們無腦遍歷了s的所有子字串並分別檢查是否為回文數。其實並不需要這麼做,舉例來說,'ab'並不是一個回文字。那麼,'xaby',無論x與y相同或者不同,都不可能是一個回文字。
換言之,從字串的某個位置m作為對稱的中心,開始往左右兩端檢查是否為回文字,就可以一次檢查所有以m為中心、左右對稱的範圍內是否為回文字。
以s = 'abcbd' 為例:
s = 'abcbd'
01234
m
指定中間位置為0
取出s[0:1] = 'a' # 是
指定中間位置為「0和1中間」
取出s[0:2] = 'ab' # 不是<結束檢查>
指定中間位置為1
取出s[1:2] = 'b' # 是
取出s[0:3] = 'abc' # 是
指定中間位置為「1和2中間」
取出s[1:3] = 'bc' # 不是<結束檢查>
指定中間位置為2
取出s[2:3] = 'c' # 是
取出s[1:4] = 'bcb' # 是
取出s[0:5] = 'abcbd' # 不是<結束檢查>
.
.
.
依此類推直到檢查完所有的子字串中間位置
這樣的策略,跟一開始的暴力解相比有兩個優點:
實作如下例:
class Solution:
def longestPalindrome(self, s: str) -> str:
LPS = s[0]
maxSpr = 0
t = '#' + ('#').join(char for char in s) + '#'
for mid in range(0, len(t)):
for spread in range(1,min(mid+1, len(t)-mid)):
if t[mid-spread] != t[mid+sread]:
break
if spread > maxSpr:
LPS = t[mid-spread: mid+spread + 1]
maxSpr = spread
return ''.join(LPS.split('#'))
這邊還用了一個資料前處理的小技巧:在s的頭尾和中間,每隔一個字母就插入一個原字串不存在的符號'#'。
這麼做的目的是為了讓index比較好指定,字母數為奇、偶數的母字串不用分兩個迴圈寫。
例如'bb'和'bab',字母數前者是偶數,後者是奇數,這樣檢查時的起點就不同。
插入'#'之後分別變成'#b#b#'和'#b#a#b#',字母數都是奇數,就可以從中間開始檢查。
最後再將插入的'#'消除即可。由於只在演算法開頭和結尾各做一次,不會影響時間複雜度。
下圖表達了整個過程:
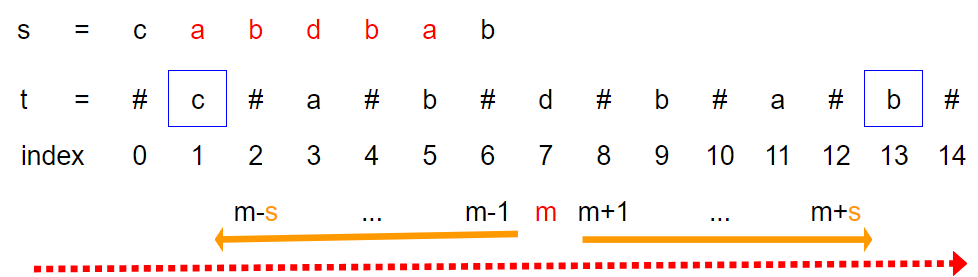
由左向右移動中心的的mid,並且逐漸增加spread,並且比較m+s、m-s位置的字母是否相同。如果相同,代表是回文數,繼續往外展開,如果不符,代表已不是回文數,結束這一組,並且移動m,重新從中間開始檢查
時間複雜度 = 子字串數 x 判斷是否為回文數的計算複雜度
本題的子字串數 = O(n^2),判斷是否為回文數的計算複雜度 = O(1),因此總複雜度 = O(n^2)
到這裡已經有點動態規劃的味道了!我們將相同中心的子字串分為同一組,並且每一組由小到大檢查,讓較大的子字串使用較小子字串的判斷結果,從而降低「判斷是否為回文字」的複雜度。最終將整體的時間複雜度降了一個維度。
不過,這還不是最佳的解法!
利用回文字的特性,我們甚至不需檢查所有的子字串
觀察這個字串:s = 'abacaba'
如果已知s[0:3] = 'aba'是回文字,且s[0:7] = 'abacaba'也是回文字,那麼不須重新做任何判斷,就可以知道s[4:7] = 'aba'必定是回文字。
為什麼呢?因為回文字有對稱的性質:
s = abacaba 是一個回文字,因此對其中心點index=3對稱
aba|aba
利用這個特性的動態規劃演算法又名Manacher’s Algorithm
首先我們先對s字串做一點處理:
頭尾接上一個「不同」的符號$ 和 ^
這是為了後續的程式碼設計方便,避免index out of range。
因為在Manacher’s Algorithm中也使用spread from mid的做法,我們一旦比對到「相同」的字元就會繼續往外比對,因此故意在頭尾加上不同的(且s中沒有出現的)字元,便可以確保比對到頭、尾時停止比對,不需要額外做邊界判定。
比起時時刻刻對index加上上下界,這種作法更簡潔。
將每個字元中間插入一個「相同」的符號
在spread from mid時我們發現,對於奇數長度的回文字和偶數長度的回文字,處理index時的做法稍微有所不同。
把每個字元中間加上一個符號,讓原本長度為偶數的回文字串,長度也變成奇數。
例如abba,插入'#'後就變成#a#b#b#a#。
經過處理之後,s字串被改寫為t。此時定義z value:
以某字元為中心,往外延伸可以得到最長的回文字時,所延展的長度稱為z。即對於該字元為中心來說,最長的回文字串長度為2z+1。
我們以一個List p來記錄,其中p[i]表示以t[i]為回文字中心時的z value

觀察可知,對於每個回文中心i,z = p[i](其z value)所對應的局部最長回文字為:
LPS = s[(i-z)//2:(i+z)//2]
s = bab
↓ i=4
$#b#a#b#^
↑ ↑
z=p[i]=3
以i=4為中心的最長回文字
LPS = s[(4-3)//2 : (4+3)//2] = s[0:3] = 'aba'
在所有位置中找出z值最大的,就能找到所對應原始字串s中最長的回文字。
那如何利用回文字對稱的特性,在O(n)時間內計算出所有位置的z值呢?
我們由左至右逐一計算p[i],並且追蹤兩個數值:
目前為止「抵達最右邊」的回文字,記錄其字尾的位置 r
目前為止 「抵達最右邊」的回文字的中心位置c
以上圖的字串為例,假設我們目前計算到 i=5,準備計算i=6。
此時,抵達最右邊的回文字串為#b#a#b#,r=7,c=4

如果照著spread from mid(鏡像法)的思維,此時我們應該比較:是否t[5]==t[7]。

但其實不需要比較!
因為t[7]包含在「抵達最右邊的回文字串」(黃底範圍)中,所以:t[5~7]和t[3~1]是互相對稱的。
所以,我們檢查與i=6對稱的位置i=2,並且查看已經計算過的z index:p[2]=1,這個1代表::
以i=2為中心,最長有一個向外延展1的回文字
因為對稱,所以:
以i=6為中心,最長「至少」有一個向外延展1的回文字
注意這裡不是「最長延展1」,而是「最長至少延展1」,原因是:
i=6延展1之後已經到7,而這個7是「目前為止抵達最右邊的回文字其字尾的位置」(r),換言之,i=8目前還從未被考慮過(黃底範圍外)。
透過以上討論,對於p[6](i=6 的 z index),不須比較是否t[5]==t[7],直接從是否t[4]==t[8]開始比較。

這個策略,可以整理如下:
對字串s做處理,轉化為字串t
p[i]紀錄以位置i為中心的 z index
對於i=0,p[i]=0
從i=1開始逐次往右計算,並且記錄抵達最右的回文字串的中心c與最右位置r
i>=r,因為i的右邊已經超過目前所探索的範圍,直接以i為中心,從i+1開始進行spread from mid策略
i<r:
c為軸,i的對稱點j
p[j]即為p[i]的最小值
i+p[j]<r:代表整個以j為中心的最長回文字都已探索過,因此以i為中心的最長回文字也在r的範圍內,因此p[i]=p[j]
i+p[j]>=r,從r+1開始以i為中心進行spread from mid策略
c與r
在迭代的過程中紀錄最大的z index(maxZ)與對應的最長回文字LPS
當中心在i且最大的回文範圍為z時,所對應原始s的最長回文子字串為s[(i-z)//2:(i+z)//2]
class Solution:
def longestPalindrome(self, s: str) -> str:
LPS, maxZ = '', 0
t = '#'.join(list(f'${s}^'))
p = [0]*len(t)
c, r = 0, 0
for i in range(1, len(t)-1):
z = r>i and min(r-i, p[2*c-i])
while t[i+(z+1)] == t[i-(z+1)]:
z+=1
p[i] = z
if i+z>r:
c,r = i, i+z
if z>maxZ:
LPS = s[(i-z)//2:(i+z)//2]
maxZ = z
return LPS
雖然看似有兩層迴圈,實際上只對每一個r進行一次字元比對,時間複雜度為O(n)
需要一個list p 來記錄所有的z value,空間複雜度亦為 O(n)

雖然本題Leetcode上給出的難度為Medium,但根據原題給出的Hint,只要求到O(n^2)的時間複雜度。

若要優化到O(n)的複雜度,則需要用到Manacher’s Algorithm這個特殊的動態規劃演算法。
對於這類較複雜的動態規劃算法,可以循序漸進的學習。我們從暴力算法中找到可以一起檢查的子字串,得到Spread from Mid的策略,並且繼續利用此策略,加上回文字鏡像對稱的特性,跳過那些不用檢查的子字串,就得到Manacher’s Algorithm演算法。
此外,我們也學習到一些實作時讓程式碼簡化的小技巧:
以上為Day09的內容!感謝你的閱讀,如果有不同的想法或心得,歡迎留言一同討論!
本文也同步登載在我的個人部落格,記錄我的學習筆記與生活點滴,歡迎來逛逛。
明天會繼續看字串題型的問題。
