引言

在處理 3D 圖形的渲染時，「頂點」是一個至關重要的概念。頂點代表著 3D 空間中的一個點，它是所有幾何形狀的基本組成單位。無論是建立立方體、球體，還是更複雜的幾何體，這些形狀都可以通過一系列頂點來定義。因此，理解頂點如何作用於圖形渲染中，對於進一步學習 3D 編程至關重要。

以長方體為例，它由六個面組成，而每個面又可以被分解成兩個三角形。在 3D 渲染中，三角形是最常用的基本單位。每個三角形由三個頂點構成，這些頂點之間的連接定義了三角形的形狀和位置。

架構

在這篇文章，我們將完成昨天沒講到的轉換過程，我們可以分成兩步驟，先取得長方體的六個面，再透過面取得頂點資訊：

transformData(data){
    //......
    const vector = this.getPosition(data);
    const vertices = this.getVertices(vector);
    const attribute = new THREE.BufferAttribute(vertices, 3);
    factory.geometry.setAttribute('position', attribute);
}

• getPosition：定義形狀表面－取得每個面的向量
• getVertices：繪製形狀表面－取得每個面需要的三角形片段

將任務分開的好處在於，我們讓程式碼更具可讀性和可維護性，未來要製作其他形狀就會更方便。

頂點

接下來，從如何繪製四邊形開始，首先回顧我早期寫的簡短版本，這個版本用二維陣列來儲存立方體的面和座標，操作起來相當直覺，將四邊形分成兩個三角形，依序組合成 [0, 1, 2] 和 [0, 2, 3] 兩個三角形。

getVertices(vector){
    const vertices = [];
    for(let M = 0; M < vector.length;M++){
        // 每個立方體有 6 個面，每個面有 4 個頂點 (共 24 個頂點)
        for(let face = 0; face < 6; face++){
            // 每個面由 2 個三角形組成
            for(let N = face*4; N < face*4 + 2; N++){
                vertices.push(...vector[M][face*4]);
                vertices.push(...vector[M][N+1]);
                vertices.push(...vector[M][N+2]);
            }
        }
    }
    return vertices;
}

然而簡短的代價是對效能的負擔，因此我們實際上需要用型別化陣列來處理，並且避免用二維陣列來額外儲存座標，以下我們先把迴圈拆開，清楚看到兩個三角形：

getVertices(vector){
    // 每個立方體 36 個頂點 (6 面 * 2 三角形/面 * 3 頂點/三角形 * 3 座標/頂點)
    const verticesCount = vector.length * 36 * 3;
    const vertices = new Float32Array(verticesCount);
    let index = 0;
    for(let M = 0; M < vector.length;M++){
        // 每個立方體有 6 個面，每個面有 4 個頂點 (共 24 個頂點)
        for(let face = 0; face < 6; face++){
            const base = face * 4 * 3;  // 每個面的起始索引

            // 第一個三角形 (點 0, 點 1, 點 2)
            vertices[index++] = vector[M][base];  // 第 0 點的 x
            vertices[index++] = vector[M][base + 1];  // 第 0 點的 y
            vertices[index++] = vector[M][base + 2];  // 第 0 點的 z

            vertices[index++] = vector[M][base + 3];  // 第 1 點的 x
            vertices[index++] = vector[M][base + 4];  // 第 1 點的 y
            vertices[index++] = vector[M][base + 5];  // 第 1 點的 z

            vertices[index++] = vector[M][base + 6];  // 第 2 點的 x
            vertices[index++] = vector[M][base + 7];  // 第 2 點的 y
            vertices[index++] = vector[M][base + 8];  // 第 2 點的 z

            // 第二個三角形 (點 0, 點 2, 點 3)
            vertices[index++] = vector[M][base];  // 第 0 點的 x
            vertices[index++] = vector[M][base + 1];  // 第 0 點的 y
            vertices[index++] = vector[M][base + 2];  // 第 0 點的 z

            vertices[index++] = vector[M][base + 6];  // 第 2 點的 x
            vertices[index++] = vector[M][base + 7];  // 第 2 點的 y
            vertices[index++] = vector[M][base + 8];  // 第 2 點的 z

            vertices[index++] = vector[M][base + 9];  // 第 3 點的 x
            vertices[index++] = vector[M][base + 10];  // 第 3 點的 y
            vertices[index++] = vector[M][base + 11];  // 第 3 點的 z
        }
    }
    return vertices;
}

• 預設情況是右手定則（逆時針）的單面渲染，所以從正面看四邊形的時候，0 1 2 3 會是逆時針，待會我們將設定成：左下、右下、右上、左上。

處理 N 邊形的頂點

接下來我們要把迴圈加回去，這樣就能拿來繪製多邊形，對於 N 邊形來說，我們需要 N - 2 個三角形片段：

getVertices(vector, totalFace = 6, totalPoint = 4){
    const totalFrament = totalPoint - 2;
    // 每個立方體 36 個頂點 (6 面 * 2 三角形/面 * 3 頂點/三角形 * 3 座標/頂點)
    const verticesCount = vector.length * totalFace * totalFrament * 3 * 3; 
    const vertices = new Float32Array(verticesCount);
    let index = 0;
    for(let M = 0; M < vector.length; M++){
        for(let face = 0; face < totalFace; face++){
            const base = face * totalPoint * 3;  // 每個面的起始索引
            for(let N = 0; N < 3 * totalFrament; N+=3){
                vertices[index++] = vector[M][base];      // 第 0 點的 x
                vertices[index++] = vector[M][base + 1];  // 第 0 點的 y
                vertices[index++] = vector[M][base + 2];  // 第 0 點的 z

                vertices[index++] = vector[M][base + 3 + N];  // 第 N+1 點的 x
                vertices[index++] = vector[M][base + 4 + N];  // 第 N+1 點的 y
                vertices[index++] = vector[M][base + 5 + N];  // 第 N+1 點的 z

                vertices[index++] = vector[M][base + 6 + N];  // 第 N+2 點的 x
                vertices[index++] = vector[M][base + 7 + N];  // 第 N+2 點的 y
                vertices[index++] = vector[M][base + 8 + N];  // 第 N+2 點的 z
            }
        }
    }
    return vertices;
}

長條圖

結構上我們定義寬度、深度，高度則表示輸入的音訊高低

getPosition(data){
    const vectors = new Array(data.length);
    const width = 2;
    const depth = this.#depth;
    for(let N = 0; N < data.length; N++){
        const height = data[N] / 3;
        const vector = new Float32Array(24 * 3);
        // 演算法
        vectors[N] = vector; 
    }
    return vectors;
}

演算法有點太長，會有排版問題，所以這邊用截圖的方式哦！

長方體的六個面

先一次性把所有座標秀出來給大家看看，以便更好地理解。並且每個面的四個點都以逆時針依序排列：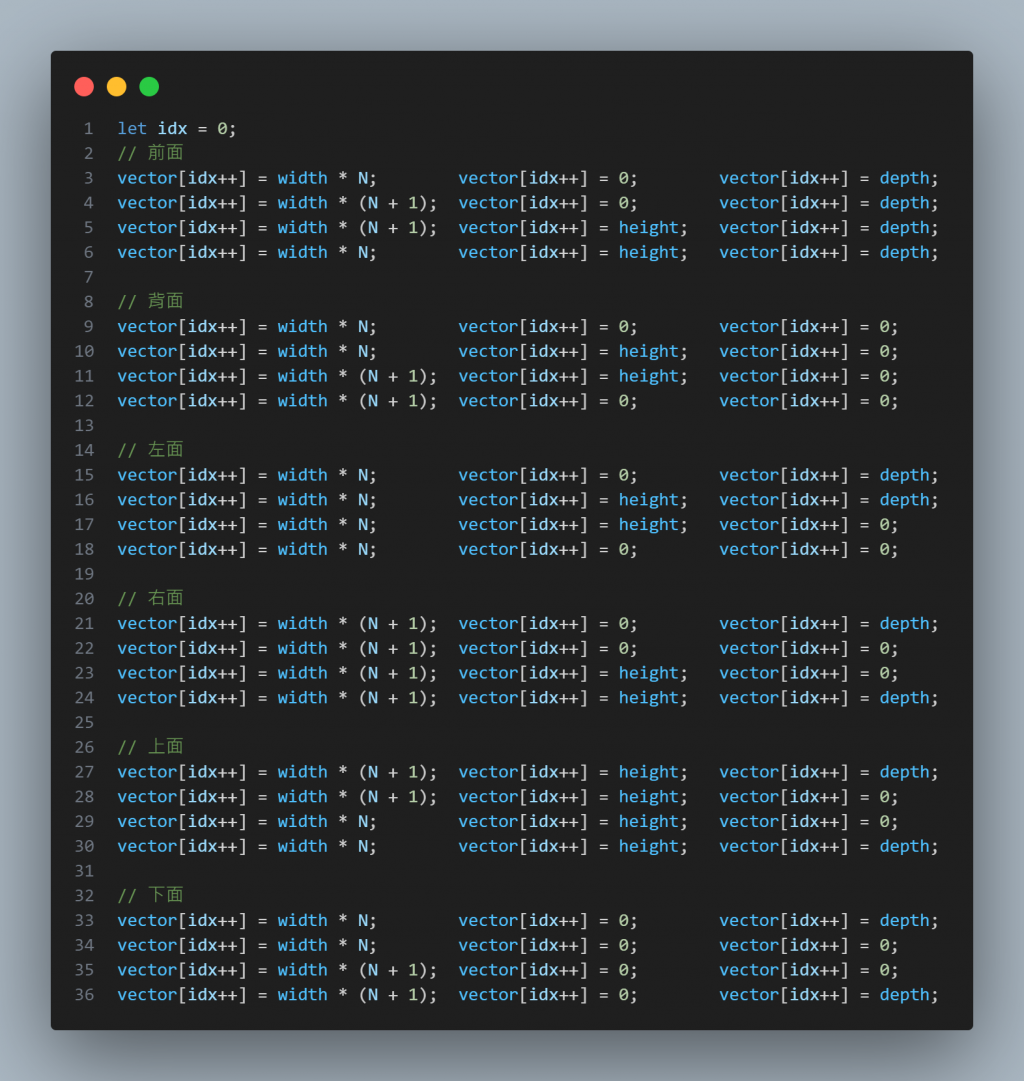

• 雖然這樣看起來很工整，但是！怎麼分得出來一個面是由那些座標組成的！

簡化邏輯－封裝八個點座標

所以，我其實是這樣做的，先把八個點封裝成 push 函式，來組織程式碼：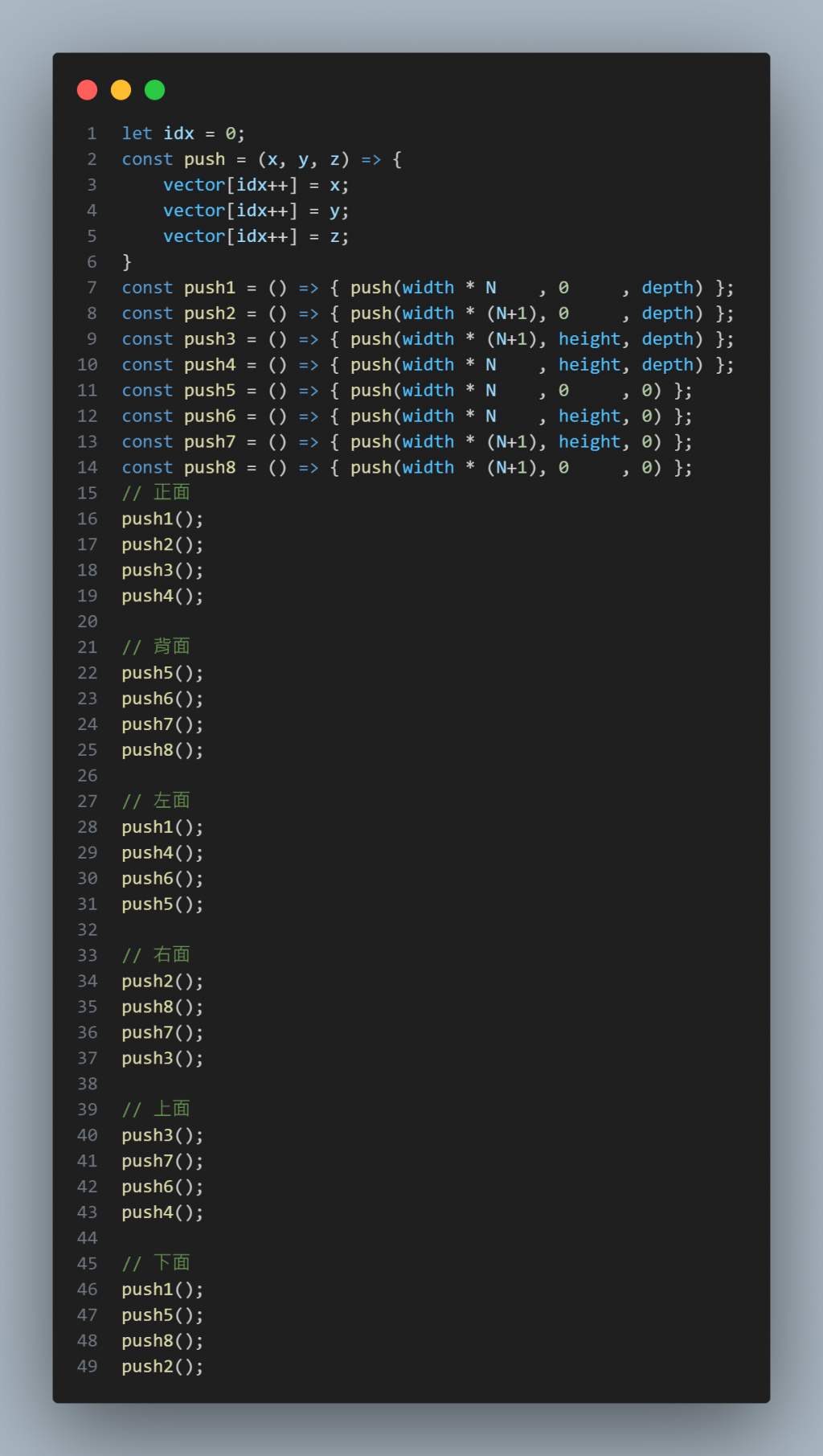

• 這樣做更容易理解，並且可以專注在點與點之間的關係，而不是座標本身

利用頂點添加顏色

接著我們同樣透過頻譜分析的數據 data，來決定長條圖的顏色，同時我們希望加入一些漸層效果，所以透過剛剛計算好的頂點位置 vertices，來設定相對的顏色，

transformData(data){
    //......
    const vector = this.getPosition(data);
    const vertices = this.getVertices(vector);

    const colorVertices = this.getColorVertices(data, vertices);
    const colorAttribute = new THREE.BufferAttribute(colorVertices, 3)
    factory.geometry.setAttribute('color', colorAttribute);
}

頂點與顏色的關聯

每個立方體由 36 個頂點構成，而這些頂點被用來決定立方體的形狀。在渲染時，我們也可以為每個頂點設定對應的顏色。主要通過幾個步驟來實現：

1. 使用音訊數據決定顏色：利用音訊頻譜的數值，計算顏色的 RGB 分量。也就是長條圖的高度
2. 動態變化，加入了一個 sin 函數來調整綠色（G）的分量，隨著時間或其他變數變化，顏色也會產生不斷的細微變化。
3. 左右側顏色差異：為了讓立方體的左右側顏色有不同的漸層，加入了 isLeft 判斷，根據立方體的位置決定該面的顏色強度。

getColorVertices(data, vertices){
    const colorVertices = new Float32Array(vertices.length);
    let colorIndex = 0;
    const width = 2;
    for (let i = 0; i < data.length; i++) {
        const value = data[i];
        
        const t = Math.sin(this.#transitionRadian);
        // 計算每個立方體的顏色
        const r = 0.200 + value / 255 * (0.816 - 0.200);
        const g = 0.329 + value / 255 * (0.590 - 0.329) * t;
        const b = 0.584 + value / 255 * (0.949 - 0.584);
    
        // 為每個立方體的 36 個頂點賦予相同的顏色
        for (let j = 0; j < 36; j++) {
            // 立方體的左側 18 個頂點
            const x = vertices[i * 36 * 3 + j * 3];
            const isLeft = (x == i * width);  
            const t = isLeft ? 1 : 0;

            const R = r + t * (0.816 - r);
            const G = g + t * (0.590 - g);
            const B = b + t * (0.949 - b);

            colorVertices[colorIndex++] = B;  // B
            colorVertices[colorIndex++] = R;  // R
            colorVertices[colorIndex++] = G;  // G
        }
    }
    return colorVertices;
}

• i * 36 * 3：立方體的索引值，每個立方體有 108 個頂點座標
• 108個座標中，j3, j3 + 1, j*3 + 2 分別表示 x, y 和 z。

來比較一下有漸層和無漸層的差別吧：

• 無漸層雖然缺乏細節，但是由於音訊不斷更新流動的特性，仍可以看到相對平滑的長條圖。

• 有了漸層後，特徵更加清晰，較容易看出長條圖的高度和變化。

結論

本文詳細介紹了如何使用頂點來控制 3D 場景中的圖形渲染與顏色表現。通過理解頂點的作用，我們不僅能夠定義圖形的幾何形狀，還能結合音訊數據動態改變顏色，進一步豐富視覺效果。

頂點的靈活性讓我們能夠對 3D 圖形進行更精確的控制，從形狀到顏色，每個細節都可以依據需求進行調整。特別是在音訊視覺化的案例中，透過頂點來應用顏色漸層與動態變化，使得視覺效果與音訊數據實時互動！

如果感興趣，可以參考 Github 上的原始碼：

• musicAnalyser.js
• bufferFactory.js