徹底理解神經網路的核心 -- 梯度下降法 (2)

neural network tensorflow gradient descent

I code so I am 2025-06-03 11:34:00 ‧ 1010 瀏覽

分享至

上一篇介紹神經網路的基本概念，這次透過簡單的範例理解梯度下降法的運作。

最簡單的神經網路

範例. 以神經網路建構攝氏與華氏溫度轉換的模型，我們收集7筆資料如下：

攝氏(X)	華氏(Y)
-40	-40
-10	14
0	32
8	46
15	59
22	72
38	100

載入套件。

import tensorflow as tf
import numpy as np

載入上述表格資料。

c = np.array([-40, -10,  0,  8, 15, 22,  38],  dtype=float)
f = np.array([-40,  14, 32, 46, 59, 72, 100],  dtype=float)

建立模型：這是全世界最簡單的神經網路，輸入為一個神經元，輸出也為一個神經元，其實就是一條簡單線性迴歸線，因為攝氏與華氏溫度轉換公式就是簡單線性迴歸。

model = tf.keras.models.Sequential([
  tf.keras.layers.Input((1,)),
  tf.keras.layers.Dense(1)
])

設定優化器(optimizer)、損失函數(loss)、效能衡量指標(metrics)的類別，注意下列設定：

損失函數模型是預測連續值，故改採均方誤差(MSE)，而非上一篇的交叉熵，那適合分類(Classification)。
經實驗後，必須加大學習率(Learning rate)，優化才會加速收斂，故將Adam優化器的學習率由預設值0.001調整為0.1。
效能衡量指標(metrics)：因為是預測連續值，沒必要使用準確率(accuracy)，可刪除，不過為了讓讀者檢視，還是保留，訓練時準確率都為0。

model.compile(optimizer=optimizer=tf.keras.optimizers.Adam(0.1),
  loss='mse',
  metrics=['accuracy'])

訓練模型：由於模型太簡單，每一週期訓練時間都很短，因此，加大訓練週期(epochs)，以追求較高的效能。

model.fit(c, f, epochs=500)

模型評分：任意設計幾筆資料測試，以下測試50及100。

x_test = np.array([50., 100.],  dtype=float)
y_test = np.array([50., 100.],  dtype=float) * 1.8 + 32
loss, accuracy = model.evaluate(x_test, y_test, verbose=False)
print(f'loss={loss:4f}, accuracy={accuracy:4f}')

繪圖觀察損失趨勢：確認是否已趨收斂。

plt.xlabel('Epochs')
plt.ylabel("Loss")
plt.plot(history.history['loss'])
plt.show()

顯示模型權重 w 及 b。

print(f'模型權重(w, b):{model.weights[0][0][0].numpy()}, 
    {model.weights[1][0].numpy()}')

繪圖比較模型與理論公式的差異：理論公式為『華氏 = 1.8 * 攝氏 + 32』，以綠色線條表示，模型公式以紅色線條表示。

import matplotlib.pyplot as plt
plt.plot(c, f, 'g')
plt.plot(c, model.predict(c, verbose=False), 'r')
plt.show()

執行

完整程式碼如下，可另存為 02_攝氏與華式溫度轉換.py。

# 攝氏與華式溫度轉換
# 載入套件
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 載入上述表格資料
c = np.array([-40, -10,  0,  8, 15, 22,  38],  dtype=float)
f = np.array([-40,  14, 32, 46, 59, 72, 100],  dtype=float)

# 建立模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Input((1,)),
  tf.keras.layers.Dense(1)
])

# 設定優化器(optimizer)、損失函數(loss)、效能衡量指標(metrics)的類別
model.compile(optimizer=tf.keras.optimizers.Adam(0.1),
  loss='mse',
  metrics=['accuracy'])

# 訓練模型
history = model.fit(c, f, epochs=500)

# 繪圖觀察損失趨勢
plt.xlabel('Epochs')
plt.ylabel("Loss")
plt.plot(history.history['loss'])
plt.show()

# 模型評分
x_test = np.array([50., 100.],  dtype=float)
y_test = np.array([50., 100.],  dtype=float) * 1.8 + 32
loss, accuracy = model.evaluate(x_test, y_test, verbose=False)
print(f'loss={loss:4f}, accuracy={accuracy:4f}')

# 顯示模型權重(w, b)
print(f'模型權重(w, b):{model.weights[0][0][0].numpy()}, \
    {model.weights[1][0].numpy()}')

# 繪圖
plt.plot(c, f, 'g')
plt.plot(c, model.predict(c, verbose=False), 'r')
plt.show()

執行：python 02_攝氏與華式溫度轉換.py。
執行結果：

損失(Loss)：即MSE，約為1.698075。
訓練至450週期，損失已趨收斂，不再明顯減少。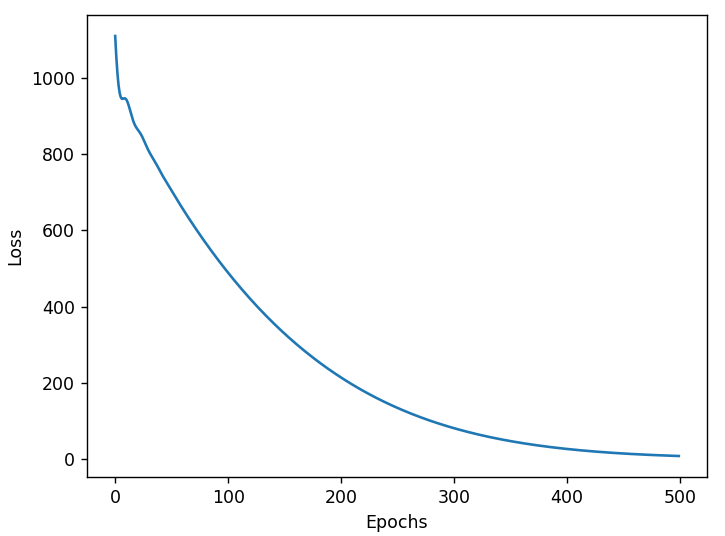
模型權重(w, b)分別為 1.8201, 29.3206，與理論公式『華氏 = 1.8 * 攝氏 + 32』略有差異。
繪圖觀察：綠線為理論公式，紅線為預測公式，差異不大。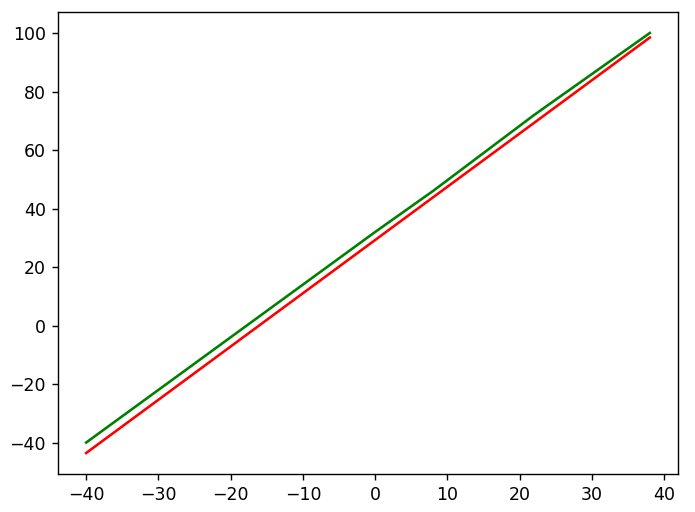

效能調校(Fine tuning)

為了讓模型更準確，可以進行效能調校，有下列方向：

蒐集更多資料。
使用更複雜的模型。
縮小學習率，並加大訓練週期。
特徵縮放，將所有特徵標準化，但本例只有1個特徵，不需進行此一步驟。

以下實驗前兩種方式。

蒐集更多資料

原來是7筆訓練資料，現在改用程式產生1000筆資料。

c = np.linspace(-100, 100, 1000)
f = c * 1.8 + 32

執行結果：模型權重(w, b):1.8000006675720215, 32.00000762939453，幾乎與理論公式相同，可見梯度下降法確實可以訓練出近乎精準的模型。

使用更複雜的模型

仍然只用7筆訓練資料，改用更複雜的模型，再加一層隱藏層(Dense)，可設定任意個數神經元，筆者設為10，模型會增加10條迴歸線，模型建構如下：

model = tf.keras.models.Sequential([
  tf.keras.layers.Input((1,)),
  tf.keras.layers.Dense(10),
  tf.keras.layers.Dense(1)
])

執行結果：

損失(Loss)：即MSE，約為0.043138，比原來的1.698075小的多。
不到100個訓練週期就收斂了。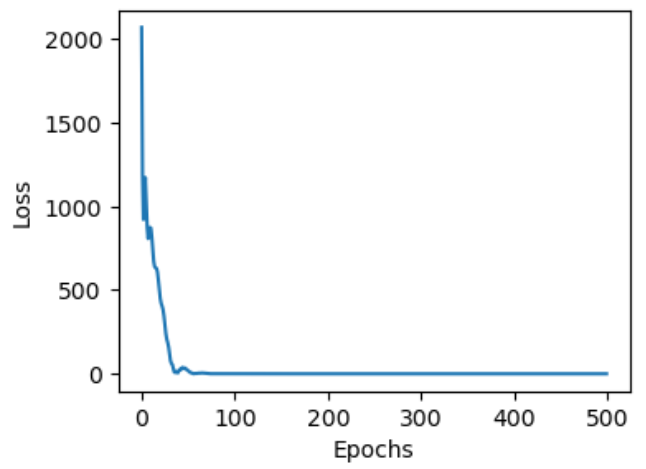
使用下列程式碼可取得每一層Dense的權重(w, b)。

# 顯示模型第1個Dense權重(w, b)
print(f'第1個Dense權重(w, b):{model.layers[0].weights[0][0].numpy()}, \
    {model.layers[0].weights[1].numpy()}')
    
# 顯示模型第2個Dense權重(w, b)
print(f'第2個Dense權重(w, b):{model.layers[1].weights[0][0].numpy()}, \
    {model.layers[1].weights[1].numpy()}')