前兩篇梯度下降法的求解都隱藏在一行程式碼 model.fit 中，這次使用自行開發實作梯度下降法，以瞭解內部求解的邏輯。

梯度下降法的作法

梯度下降法是利用正向傳導(Forward propagation)及反向傳導(Backpropagation)交互進行的方式。逐步逼近最佳解，如下圖：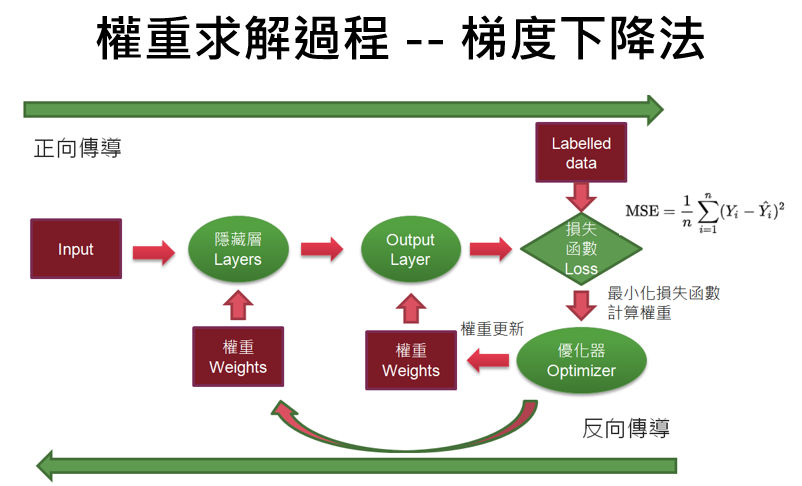

圖一. 梯度下降法的權重求解過程

步驟如下：

1. 先設定權重(w、b)為任意值。
2. 正向傳導：我們前面講過神經網路是多條迴歸線的組合，即 y = wx + b，由於w、x、b均為已知，可求得預測值(ŷ)。
3. 若損失函數為均方誤差(MSE)，即∑(y-ŷ)**2/n，則可計算，後續證明。
4. 反向傳導：梯度下降法保證沿著梯度方向更新權重，可求得最佳解。
5. 使用優化器(Optimizer)更新權重：依下列公式更新權重，其中學習率(Learning rate)可控制權重更新的幅度，可在訓練模型前設定，如前一篇的程式碼。
   調整後的權重 = 原權重 + (學習率 * 梯度)

# 設定學習率為0.1
model.compile(optimizer=optimizer=tf.keras.optimizers.Adam(0.1),
  loss='mse',
  metrics=['accuracy'])

6. 回到步驟2，反覆執行N次，N即執行週期(epoch)，可在訓練模型時設定，參見以下程式碼。

# 設定執行週期為500
model.fit(c, f, epochs=500)

MSE梯度公式推算

單一變數的變化率稱為斜率(Slope)，多變數的變化率稱為梯度(Gradient)，兩者都是一階導數，透過偏微分(Partial derivative)求解，計算如下。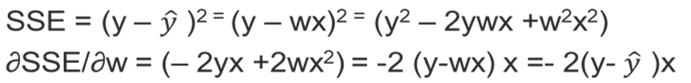

有幾點說明：

1. 梯度為-2(y-ŷ)*x，不易記憶，通常會把-2拿掉，改為(y-ŷ)*x，公式改為調整後的權重 = 原權重 - (學習率 * 梯度)。
2. 第一篇的範例【手寫阿拉伯數字辨識】，損失函數採用交叉熵(Cross entropy)，其梯度要怎麼推算公式? 不要擔心，所有的深度學習套件都提供自動微分(Automatic Differentiation)，再複雜的損失函數，都可以自動計算出梯度。

# 設定損失函數(loss)為多類別的交叉熵(Cross entropy)
model.compile(optimizer='adam',
  loss='sparse_categorical_crossentropy',
  metrics=['accuracy'])

實作

範例. 簡單損失函數求最小值。

1. 載入套件。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

2. 修正中文亂碼。

plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei'] 
plt.rcParams['axes.unicode_minus'] = False

3. 假設損失函數為 y=x²。

def func(x): return x ** 2

4. 手動微分：損失函數的一階導數為dy/dx=2*x，下一篇會改為自動微分。

# 損失函數的一階導數:dy/dx=2*x
def dfunc(x): return 2 * x

5. 梯度下降法：仔細觀察程式邏輯，即上述的求解步驟。

def train(w_start, epochs, lr):    
    """ 梯度下降法
        :param w_start: x的起始點    
        :param epochs: 訓練週期    
        :param lr: 學習率    
        :return: x在每次反覆運算後的位置（包括起始點），長度為epochs+1    
     """    
    w_list = np.zeros(epochs+1)    
    w = w_start    
    w_list[0] = w  
    # 執行N個訓練週期
    for i in range(epochs):         
        # 權重的更新W_new
        # W_new = W — learning_rate * gradient        
        w -=  dfunc(w) * lr         
        w_list[i+1] = w    
    return w_list

6. 模型訓練：呼叫梯度下降法。

w_start = -5 # 權重初始值
epochs = 150 # 訓練週期數
lr = 0.1     # 學習率
w = train(w_start, epochs, lr=lr) 
print (f'w:{np.around(w, 2)}')

7. 繪圖觀察權重更新過程。

color = 'r'    
t = np.arange(-6.0, 6.0, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(w_list, func(w_list), c=color, label='lr={}'.format(lr))    
plt.scatter(w_list, func(w_list), c=color) 
# 繪圖箭頭，顯示權重更新方向
plt.quiver(w_list[0]-0.2, func(w_list[0]), w_list[4]-w_list[0], 
    func(w_list[4])-func(w_list[0]), color='g', scale_units='xy', scale=5)
# 繪圖標題設定
font = {'family': 'Microsoft JhengHei', 'weight': 'normal', 'size': 20}
plt.title('梯度下降法', fontproperties=font)
plt.xlabel('w', fontsize=20)
plt.ylabel('Loss', fontsize=20)
plt.show()    

執行

完整程式碼如下，可另存為 05_函數的梯度下降.py。

# 載入套件
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

# 修正中文亂碼
plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei'] 
plt.rcParams['axes.unicode_minus'] = False


# 損失函數為 y=x^2
def func(x): return x ** 2

# 損失函數的一階導數:dy/dx=2*x
def dfunc(x): return 2 * x

def train(w_start, epochs, lr):    
    """ 梯度下降法
        :param w_start: x的起始點    
        :param epochs: 訓練週期    
        :param lr: 學習率    
        :return: x在每次反覆運算後的位置（包括起始點），長度為epochs+1    
     """    
    w_list = np.zeros(epochs+1)    
    w = w_start    
    w_list[0] = w  
    # 執行N個訓練週期
    for i in range(epochs):         
        # 權重的更新W_new
        # W_new = W — learning_rate * gradient        
        w -=  dfunc(w) * lr         
        w_list[i+1] = w    
    return w_list

# 模型訓練：呼叫梯度下降法 
w_start = -5 # 權重初始值
epochs = 150 # 訓練週期數
lr = 0.1     # 學習率
w_list = train(w_start, epochs, lr=lr) 
print (f'w:{np.around(w_list, 2)}')

# 繪圖觀察權重更新過程
color = 'r'    
t = np.arange(-6.0, 6.0, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(w_list, func(w_list), c=color, label='lr={}'.format(lr))    
plt.scatter(w_list, func(w_list), c=color) 
# 繪圖箭頭，顯示權重更新方向
plt.quiver(w_list[0]-0.2, func(w_list[0]), w_list[4]-w_list[0], 
    func(w_list[4])-func(w_list[0]), color='g', scale_units='xy', scale=5)

# 繪圖標題設定
font = {'family': 'Microsoft JhengHei', 'weight': 'normal', 'size': 20}
plt.title('梯度下降法', fontproperties=font)
plt.xlabel('w', fontsize=20)
plt.ylabel('Loss', fontsize=20)
plt.show()

1. 執行：python 05_函數的梯度下降.py。
2. 執行結果：

• 執行32個訓練週期，權重(w)就不再更新了，維持在0。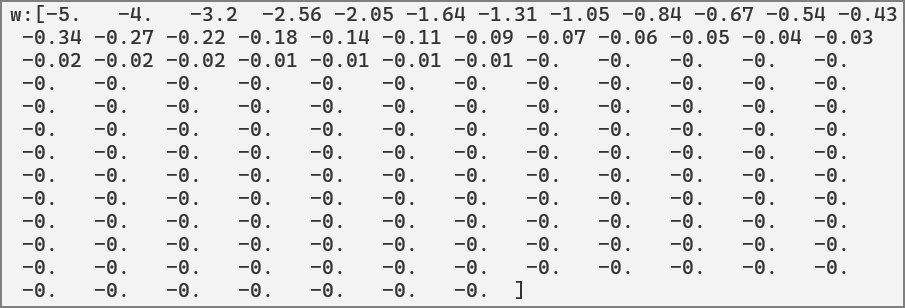
  

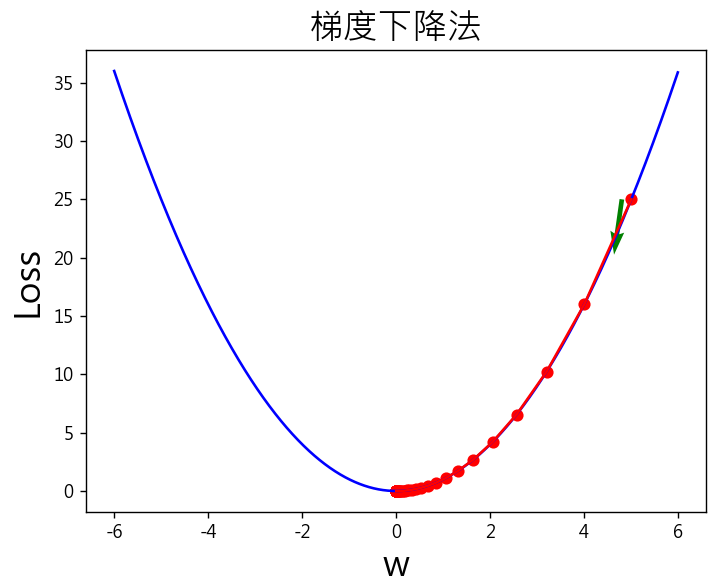
• 觀察下圖綠色箭頭，起始權重(w)設定為-5，逐步更新往函數最小值前進。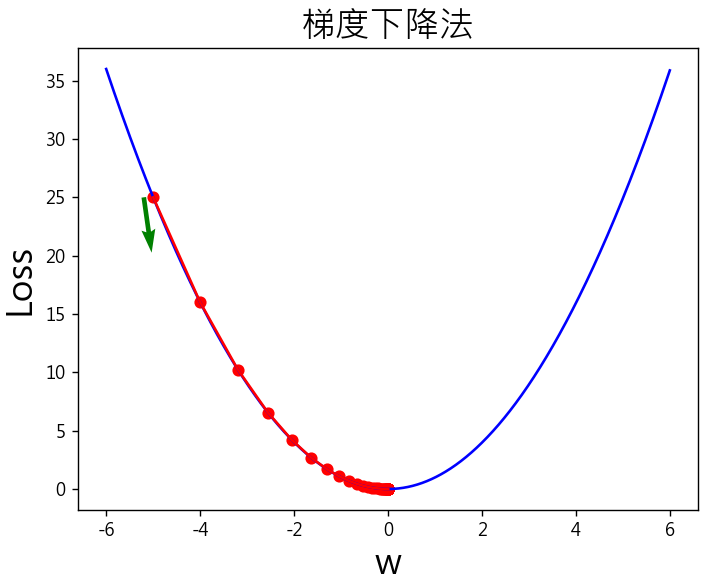
  

• 修改權重初始值(w)設定為5或任意值，再重新執行，最後權重(w)仍為0，逐步更新往函數最小值前進。

w_start = 5 # 權重初始值

• 修改學習率由0.1改為0.001，造成更新步幅過小，還沒走到最小值，訓練就結束了。

lr = 0.001     # 學習率

• 修改學習率由0.1改為0.001，並加大訓練週期數為15000，還是可以找到最小值。

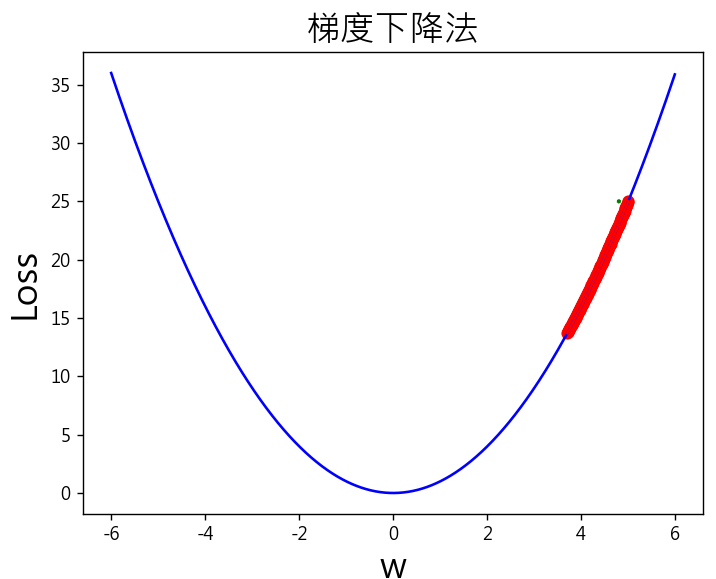
epochs = 15000 # 訓練週期數
lr = 0.001     # 學習率

結語

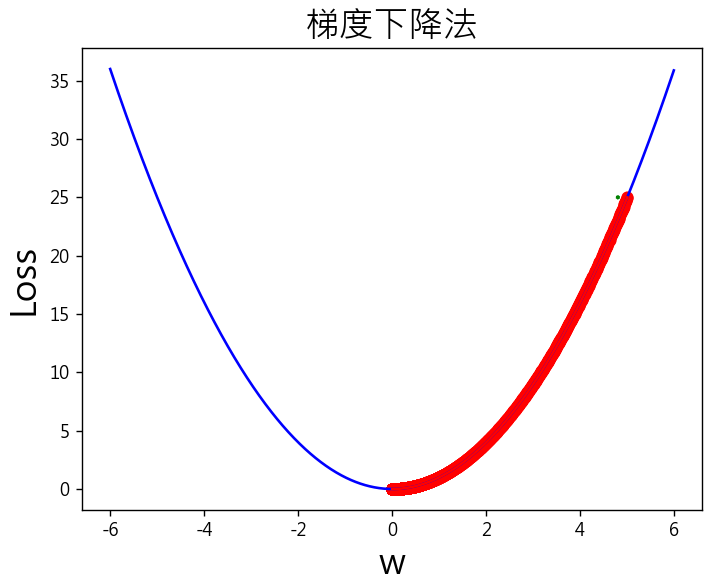
以上使用很簡單的函數y=x²為例，自行開發梯度下降法找到最佳解，如果是線性迴歸y=wx+b，要如何處理呢? 又如果有多個特徵，即多元線性迴歸，梯度更新要如何處理呢? 要使用自動微分(Automatic Differentiation)，如何修改呢? 下一篇將詳細說明作法。

Happy coding !!

工商廣告:)

《深度學習最佳入門與專題實戰》導讀講座 2025/07/11 歡迎報名

書籍：

1. 深度學習最佳入門與專題實戰：理論基礎與影像篇, 2025/05 再版
2. 深度學習最佳入門與專題實戰：自然語言處理、大型語言模型與強化學習篇, 2025/05 再版
3. 開發者傳授 PyTorch 秘笈
4. Scikit-learn 詳解與企業應用

影音課程：

深度學習PyTorch入門到實戰應用

企業包班

系列文章目錄

徹底理解神經網路的核心 -- 梯度下降法 (1)
徹底理解神經網路的核心 -- 梯度下降法 (2)
徹底理解神經網路的核心 -- 梯度下降法 (3)
徹底理解神經網路的核心 -- 梯度下降法 (4)
徹底理解神經網路的核心 -- 梯度下降法 (5)