上篇探討學習率的調整，接著討論優化器對模型訓練的影響。

優化器(Optimizer)

優化(Optimization)是以最小化損失函數為目標，尋找模型參數的最佳解，故優化器(Optimizer)就是負責執行的程式，它主要有兩個任務：

1. 計算梯度。
2. 權重的更新：開發者可以設定各式優化器類別，內含學習率(learning rate)設定，還有其他參數會對梯度更新的幅度進行自動調適(Adaptive)。
   調整後的權重 = 原權重 + 學習率(Learning Rate) * 梯度(Gradient)

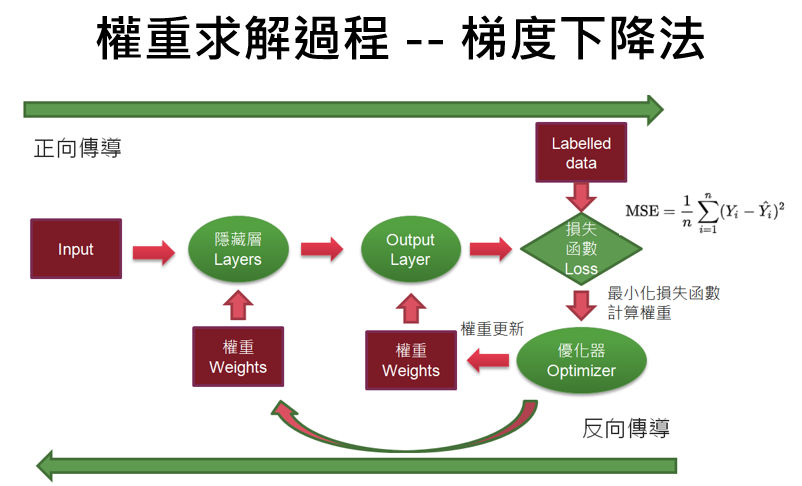
圖一. 梯度下降法的權重求解過程

TensorFlow提供許多優化器如下，可詳閱Keras Optimizer 官方文件說明，我們介紹以下兩種。

1. 隨機梯度下降法(Stochastic Gradient Descent, SGD)：不只是單純的mini-batch梯度下降，還額外提供動能(Momentum)調整的機制。參閱Keras SGD 官方文件說明，公式如下：

速度(velocity) = 動能(momentum) * 速度(velocity) - 學習率(learning rate) * 梯度(gradient)
w = w + 速度(velocity)

若參數nesterov=True，公式如下：

速度(velocity) = 動能(momentum) * 速度(velocity) - 學習率(learning rate) * 梯度(gradient)
w = w + momentum * 速度(velocity) - 學習率(learning rate) * 梯度(gradient) 

2. Adam：為避免SGD過衝(overshoot)，跳過全局最小值，Adam依據一階(beta_1)及二階(beta_2)動能進行自動調適，參閱論文的虛擬碼如下：
   

不管是SGD或Adam，增加動能(momentum)的主要目的都是希望能跳過區域最小值(Local minimum)，進而找到全局最小值(Global minimum)，當梯度越陡峭，動能越大，即更新幅度越大，以跳過區域最小值，如圖三，梯度很陡峭(①)，產生很大的動能(②)，更新幅度一舉跳過區域最小值，找到全局最小值(③)。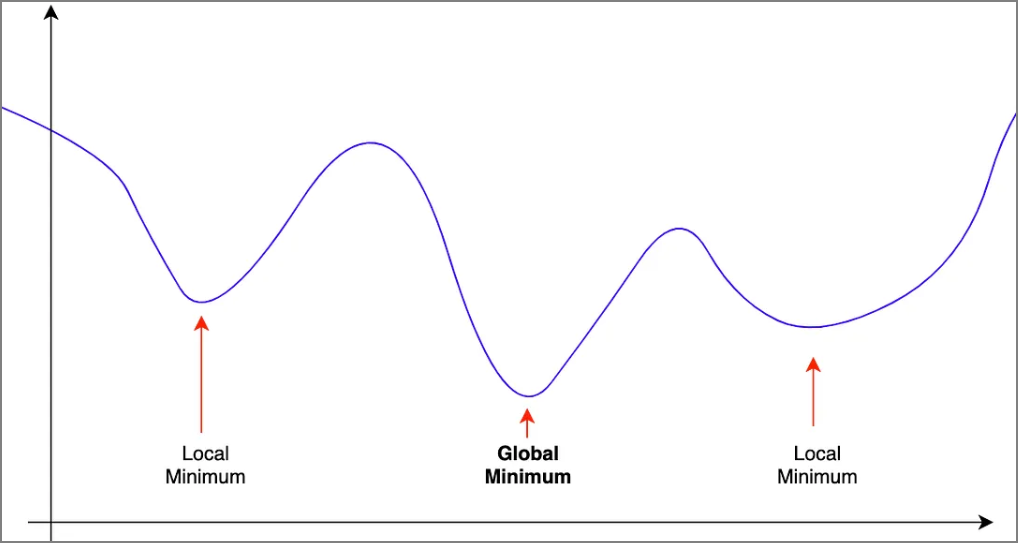

圖二. 區域最小值(Local minimum) vs. 全局最小值(Global minimum)

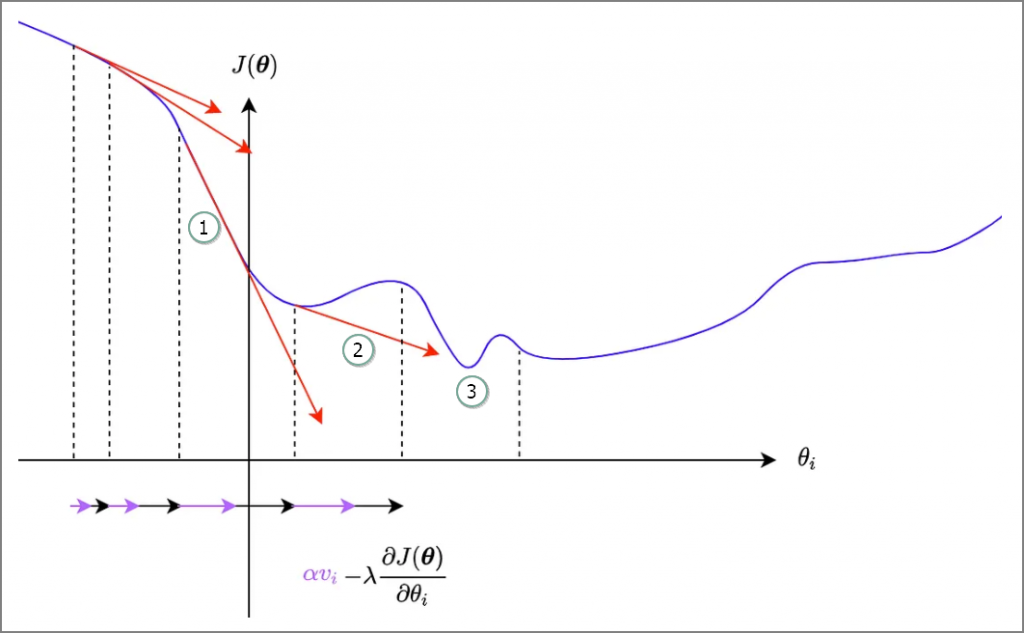
圖三. 梯度越陡峭，動能越大，圖片來源：Gradient Descent Optimizers

如果損失函數是單純的凸集合(Convex)，那一般的梯度下降法就可以輕鬆的找到最小值，但大部分深度學習使用的資料集特徵個數都很多，例如MNIST就有784個特徵，我們根本無法想像784度空間的資料分佈是何種函數，有學者Ankur Mohan製作一個視覺化的網頁，將各種知名的預訓模型(Pre-trained models)損失景觀描繪出來如下，到處都有區域最小值，要找到全局最小值何其困難，因此，才會有那麼多的優化器論文發表，一般範例常用Adam優化器，因為它在大部分的狀況下表現良好。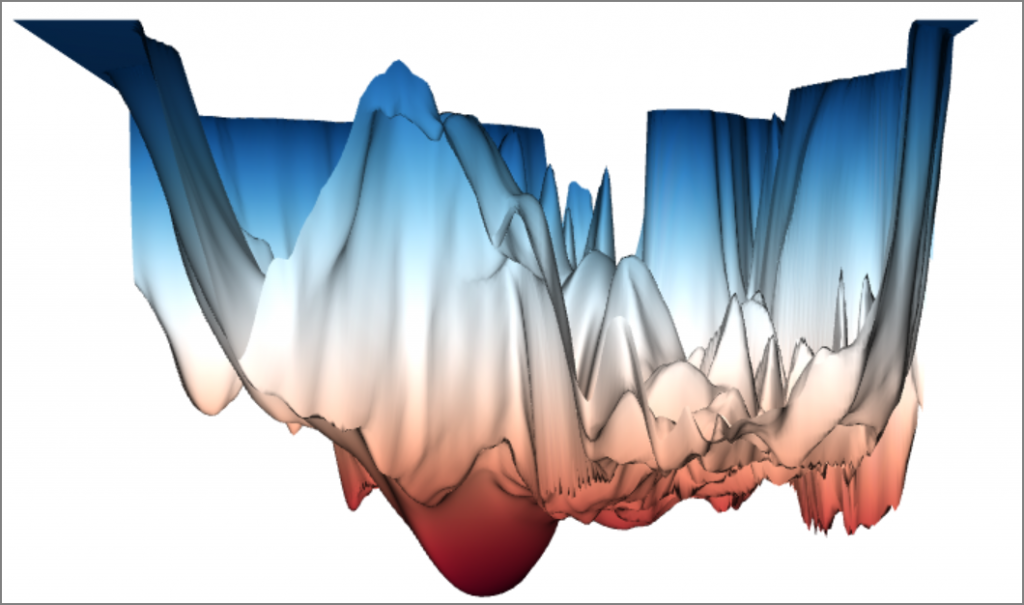

圖四. 視覺化的網頁Loss landscape visualizer

簡單實作

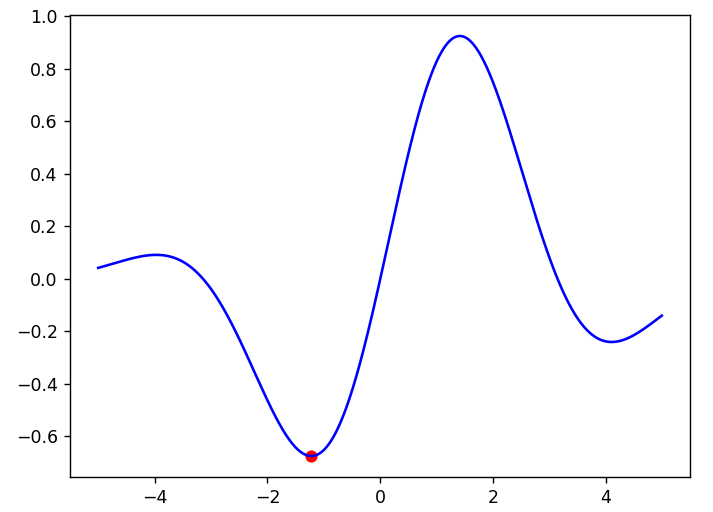
範例1. 區域最小值(Local minimum) vs. 全局最小值(Global minimum)，損失函數如下：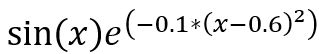

1. 修改08_以自動微分實作梯度下降.py部分內容。
2. 先定義損失函數。

def func(x): tf.sin(w)*tf.exp(-0.1*(w-0.6)**2)

3. 修改train函數。

def train(w_start, epochs, lr):    
    w_list = np.array([])    
    w = tf.Variable(w_start)         # 宣告 TensorFlow 變數(Variable)
    w_list = np.append(w_list, w_start)  
    # 執行N個訓練週期
    for i in range(epochs):         
        with tf.GradientTape() as g: # 自動微分
            y = tf.sin(w)*tf.exp(-0.1*(w-0.6)**2) # 損失函數

        dw = g.gradient(y, w) # 取得梯度
        # 更新權重：新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)
        w.assign_sub(lr * dw)  # w -=  dw * lr         
        w_list = np.append(w_list, w.numpy())    
    return w_list

4. 完整程式碼如下，另存為 19_global_minimum.py。

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf 

# 損失函數
def func(x): return np.sin(x)*np.exp(-0.1*(x-0.6)**2)

def train(w_start, epochs, lr):    
    w_list = np.array([])    
    w = tf.Variable(w_start)         # 宣告 TensorFlow 變數(Variable)
    w_list = np.append(w_list, w_start)  
    # 執行N個訓練週期
    for i in range(epochs):         
        with tf.GradientTape() as g: # 自動微分
            y = tf.sin(w)*tf.exp(-0.1*(w-0.6)**2) # 損失函數

        dw = g.gradient(y, w) # 取得梯度
        # 更新權重：新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)
        w.assign_sub(lr * dw)  # w -=  dw * lr         
        w_list = np.append(w_list, w.numpy())    
    return w_list

# 權重初始值
# w_start = 0.3  # 找到全局最小值(Global minimum)   
w_start = 5.0  # 找到區域最小值(Local minimum)
# 執行週期數
epochs = 1000 
# 學習率   
lr = 0.01   
# 梯度下降法 
# *** Function 可以直接當參數傳遞 ***
w = train(w_start, epochs, lr=lr) 
print (w)
# 輸出：[-5.     -2.     -0.8    -0.32   -0.128  -0.0512]

color = 'r'    
#plt.plot(line_x, line_y, c='b')    
from numpy import arange
t = arange(-5, 5, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(w, func(w), c=color, label='lr={}'.format(lr))    
plt.scatter(w, func(w), c=color, )    
plt.legend()
plt.show()

9. 執行：python 19_global_minimum.py。

10. 執行結果：權重初始值設為5.0，只能找到區域最小值(Local minimum)。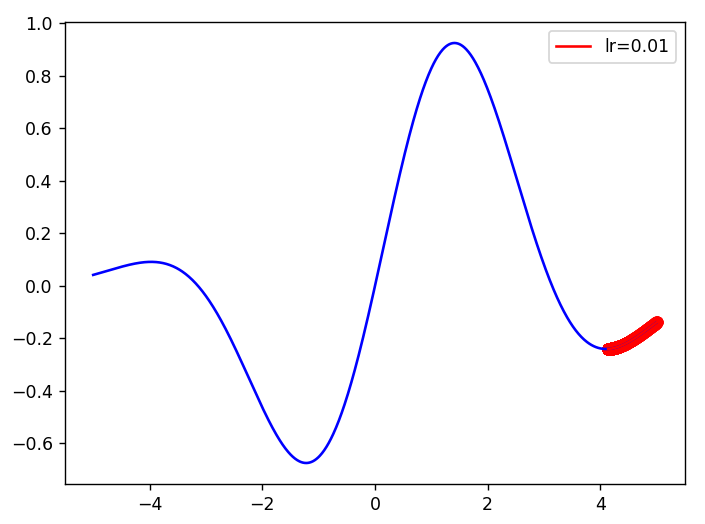
    )。

11. 修改權重初始值設為0.3，可以找到找到全局最小值(Global minimum)。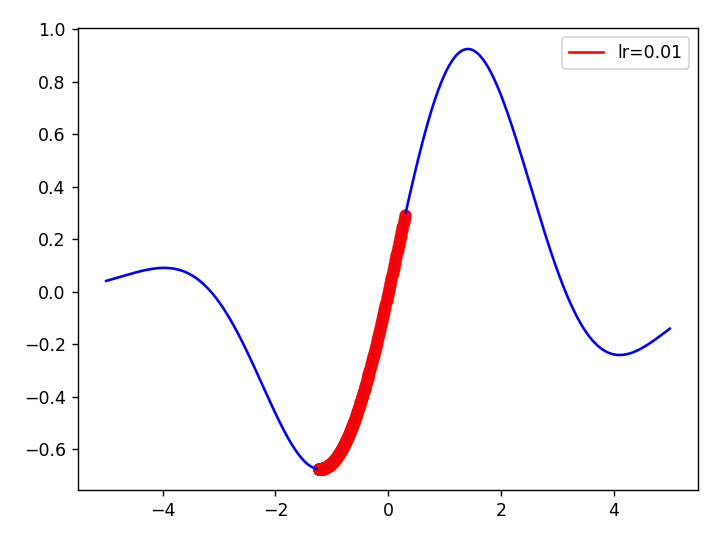
    

範例2. 使用隨機設定權重初始值，以尋找全局最小值(Global minimum)。

1. 修改19_global_minimum.py部分內容。
2. 修改train函數：在[-10.0, 10.0]之間，隨機設定權重初始值。

# 損失函數
def func(x): return np.sin(x)*np.exp(-0.1*(x-0.6)**2)

def train(func, restarts=10, steps=1000, lr=0.01, x_range=(-10.0, 10.0)):
    best_loss = float('inf')
    best_x = None

    for i in range(restarts):
        # Randomly initialize x within the specified range
        x = tf.Variable(tf.random.uniform(shape=(), minval=x_range[0], maxval=x_range[1]
            , dtype=tf.float64))

        for step in range(steps):
            with tf.GradientTape() as tape:
                loss = func(x)
            grad = tape.gradient(loss, x)
            x.assign_sub(lr * grad)  # Gradient descent update

        final_loss = func(x).numpy()
        print(f"Restart {i+1}: x = {x.numpy():.4f}, loss = {final_loss:.4f}")

        if final_loss < best_loss:
            best_loss = final_loss
            best_x = x.numpy()

    return best_x, best_loss

3. 完整程式碼如下，另存為 20_global_minimum_with_optimizer1.py。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 損失函數
def func(x):
    # return x**2 + 10.0 * tf.sin(x)
    return tf.sin(x)*tf.exp(-0.1*(x-0.6)**2) 

# 模型訓練函數
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf 

# 損失函數
def func(x): return np.sin(x)*np.exp(-0.1*(x-0.6)**2)

def train(w_start, epochs, lr):    
    w_list = np.array([])    
    w = tf.Variable(w_start)         # 宣告 TensorFlow 變數(Variable)
    w_list = np.append(w_list, w_start)  
    # 執行N個訓練週期
    for i in range(epochs):         
        with tf.GradientTape() as g: # 自動微分
            y = tf.sin(w)*tf.exp(-0.1*(w-0.6)**2) # 損失函數

        dw = g.gradient(y, w) # 取得梯度
        # 更新權重：新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)
        w.assign_sub(lr * dw)  # w -=  dw * lr         
        w_list = np.append(w_list, w.numpy())    
    return w_list

# 權重初始值
# w_start = 0.3  # 找到全局最小值(Global minimum)   
w_start = 5.0  # 找到區域最小值(Local minimum)
# 執行週期數
epochs = 1000 
# 學習率   
lr = 0.01   
# 梯度下降法 
# *** Function 可以直接當參數傳遞 ***
w = train(w_start, epochs, lr=lr) 
print (w)
# 輸出：[-5.     -2.     -0.8    -0.32   -0.128  -0.0512]

color = 'r'    
#plt.plot(line_x, line_y, c='b')    
from numpy import arange
t = arange(-5, 5, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(w, func(w), c=color, label='lr={}'.format(lr))    
plt.scatter(w, func(w), c=color, )    
plt.legend()
plt.show()

4. 執行：python 20_global_minimum_with_optimizer1.py。

5. 執行結果：權重初始值設為5.0，原來只能找到區域最小值，改隨機設定權重初始值，即可找到找到全局最小值(Global minimum)。
   
   

6. 可以改用其他損失函數試試看，例如：

def func(x):
    return x**2 + 10.0 * tf.sin(x)

神經網路實作

範例3. 使用隨機生成的訓練資料，尋找全局最小值，大部分程式與範例2相似。

1. 完整程式碼如下，另存為 20_global_minimum_with_optimizer2.py。

# 載入套件
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 生成訓練資料
np.random.seed(0)
x_data = np.linspace(-2 * np.pi, 2 * np.pi, 200).reshape(-1, 1)
y_data = np.sin(x_data) + 0.1 * np.random.randn(*x_data.shape)

# 模型
def build_model():
    model = tf.keras.Sequential([
        tf.keras.layers.Dense(64, activation='tanh', input_shape=(1,)),
        tf.keras.layers.Dense(64, activation='tanh'),
        tf.keras.layers.Dense(1)
    ])
    return model

# 模型訓練函數
def train(x, y, restarts=5, epochs=200, batch_size=32):
    best_loss = float('inf')
    best_model = None

    for i in range(restarts):
        print(f"Restart {i + 1}/{restarts}")
        model = build_model()
        model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.01),
                      loss='mse')

        history = model.fit(x, y, epochs=epochs, batch_size=batch_size, verbose=0)
        final_loss = history.history['loss'][-1]

        print(f"  Final loss: {final_loss:.4f}")
        if final_loss < best_loss:
            best_loss = final_loss
            best_model = model

    return best_model, best_loss

# 特徵縮放
x_norm = (x_data - np.mean(x_data)) / np.std(x_data)

# 模型訓練
best_model, best_loss = train(x_norm, y_data, restarts=5)
print(f"\nBest loss after restarts: {best_loss:.4f}")

y_pred = best_model.predict(x_norm)

# 繪圖
plt.figure(figsize=(10, 5))
plt.scatter(x_data, y_data, label='Noisy Data', s=10)
plt.plot(x_data, y_pred, color='red', label='NN Prediction', linewidth=2)
plt.legend()
plt.title("Fitting a Noisy Sine Wave using Neural Network")
plt.grid(True)
plt.show()

4. 執行：python 20_global_minimum_with_optimizer2.py。
5. 執行結果：不需隨機設定權重初始值，模型梯度會保留，重複訓練，即可找到找到全局最小值(Global minimum)。
   
   

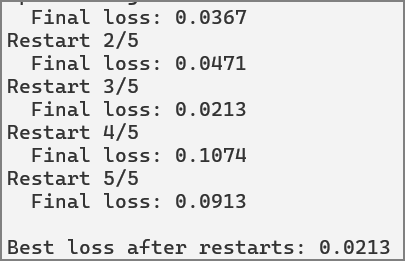
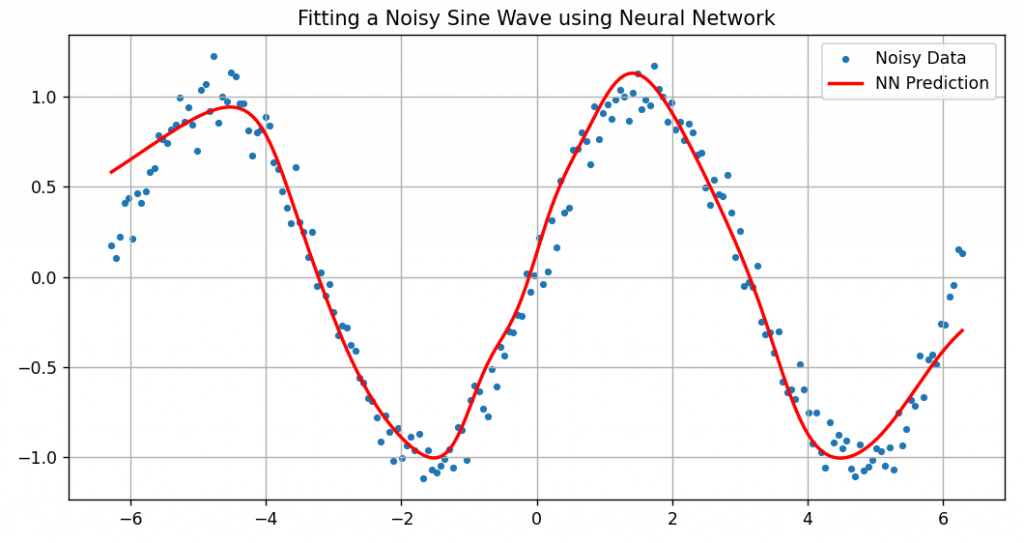
範例4. 在訓練過程中取得優化器的學習率及動能(Momentum)。

1. 在訓練過程中透過以下程式碼可取得學習率變化。

    optimizer._get_current_learning_rate().numpy()

2. 在訓練過程中透過以下程式碼可取得動能(Momentum)變化。

    for var in optimizer.variables:
        if 'momentum' in var.name:
            mean_vel = tf.reduce_mean(tf.abs(var)).numpy()
            print(f"  {var.name}: {mean_vel:.6e}")

3. 完整程式碼如下，另存為 22_get_momentum_with_mnist_自動微分.py。

# 手寫阿拉伯數字辨識
# 載入套件
import tensorflow as tf
# 載入手寫阿拉伯數字訓練資料(MNIST)
mnist = tf.keras.datasets.mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()
y_train = tf.one_hot(y_train, depth=10)
y_test = tf.one_hot(y_test, depth=10)

# 特徵縮放
x_train, x_test = x_train / 255.0, x_test / 255.0

# 建立模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Input((28, 28)),
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])

# 設定優化器(optimizer)、損失函數(loss)
optimizer = tf.keras.optimizers.Adam()
loss_fn = tf.keras.losses.CategoricalCrossentropy() #from_logits=True)

# 訓練模型
epochs = 5
batch_size = 1000
for epoch in range(epochs):
    for batch in range(x_train.shape[0] // batch_size):
        x_batch = x_train[batch * batch_size : (batch + 1) * batch_size]
        y_batch = y_train[batch * batch_size : (batch + 1) * batch_size]

        with tf.GradientTape() as tape:
            # Forward pass
            pred = model(x_batch)
            # Calculate the loss
            loss = loss_fn(y_batch, pred)

        # Calculate gradients
        gradients = tape.gradient(loss, model.trainable_variables)

        # Update model weights
        optimizer.apply_gradients(zip(gradients, model.trainable_variables))

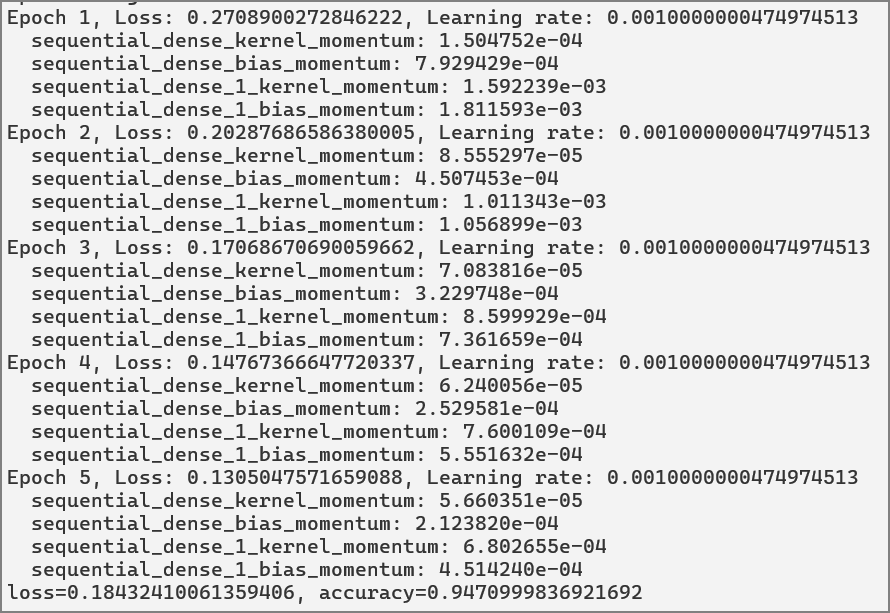
    print(f"Epoch {epoch+1}, Loss: {loss.numpy()}, Learning rate: {optimizer._get_current_learning_rate().numpy()}")
    for var in optimizer.variables:
        if 'momentum' in var.name:
            mean_vel = tf.reduce_mean(tf.abs(var)).numpy()
            print(f"  {var.name}: {mean_vel:.6e}")

# 模型評分
model.compile(optimizer=optimizer, loss=loss_fn, metrics=['accuracy'])
loss, accuracy = model.evaluate(x_test, y_test, verbose=False)
print(f'loss={loss}, accuracy={accuracy}')    

4. 執行：python 22_get_momentum_with_mnist_自動微分.py。
5. 執行結果：

• sequential_dense_kernel_momentum：第一層Dense的w動能。
• sequential_dense_bias_momentum：第一層Dense的b動能。
• sequential_dense_1_kernel_momentum：第二層Dense的w動能。
• sequential_dense_1_bias_momentum：第二層Dense的b動能。
• 學習率設定是固定值，為0.001。
  

6. 可以將學習率設定為變動值，例如：

lr_schedule = tf.keras.optimizers.schedules.CosineDecayRestarts(
    initial_learning_rate=0.001,
    first_decay_steps=10,
    t_mul=2.0,
    m_mul=0.9,
    alpha=0.0
)
optimizer = tf.keras.optimizers.Adam(learning_rate=lr_schedule)

結語

筆者試圖透過優化器選用，要能達到圖三的效果，但是，測試一天都失敗，最後求助ChatGPT，才完成上述範例，都是隨機設定權重初始值，而非選用適當的優化器。

另外，各種優化器的收斂速度會因訓練資料有所不同，可以參閱『關於深度學習優化器 optimizer 的選擇，你需要了解這些 』的動畫。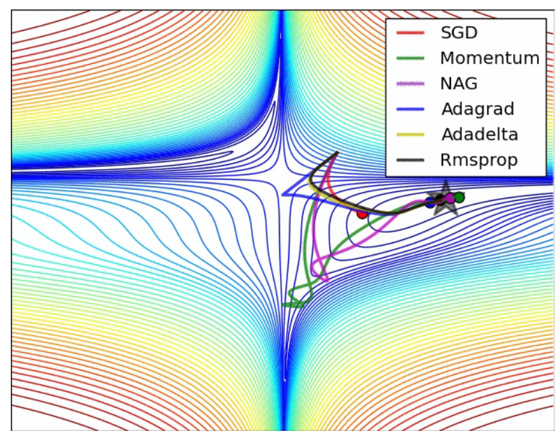

工商廣告:)

《深度學習最佳入門與專題實戰》導讀講座 2025/07/11 歡迎報名

書籍：

1. 深度學習最佳入門與專題實戰：理論基礎與影像篇, 2025/05 再版
2. 深度學習最佳入門與專題實戰：自然語言處理、大型語言模型與強化學習篇, 2025/05 再版
3. 開發者傳授 PyTorch 秘笈
4. Scikit-learn 詳解與企業應用

影音課程：

深度學習PyTorch入門到實戰應用

企業包班

系列文章目錄

徹底理解神經網路的核心 -- 梯度下降法 (1)
徹底理解神經網路的核心 -- 梯度下降法 (2)
徹底理解神經網路的核心 -- 梯度下降法 (3)
徹底理解神經網路的核心 -- 梯度下降法 (4)
徹底理解神經網路的核心 -- 梯度下降法的應用 (5)
梯度下降法(6) -- 學習率動態調整
梯度下降法(7) -- 優化器(Optimizer)
梯度下降法(8) -- Activation Function
梯度下降法(9) -- 損失函數
梯度下降法(10) -- 總結