在前面我們已經接觸過「神經網路」的大致結構，
裡面最重要的角色之一就是 神經元（Neuron）。

神經元本身就像是一個「小小的數學單元」，它會接收輸入（input），
在經過一連串計算後，最後輸出一個結果。
而這個「輸出的形式」會決定整個神經網路能不能學會複雜的模式。

這裡就牽涉到一個非常關鍵的概念 - 激活函數（Activation Function） 。

(也有人叫它啟動函數、激勵函數，但為了統一我在文章中會統一稱它為激活函數，
事實上他們指的都是Activation Function這個函數，讀者不用擔心混淆。)

我們可以把激活函數想像成「神經元的大腦開關」，
它會決定輸入訊號要如何轉換成輸出。

如果沒有這些函數，整個神經網路就會退化成一個很單純的「數學線性公式」，
無法學習像是影像辨識、語音識別這種複雜的問題。

而今天我們就要仔細去了解三個最常見的激活函數：
「Sigmoid」 、 「ReLU」 、 「Softmax」 。

Sigmoid：輸出在 0 到 1 之間的平滑函數

Sigmoid 是最早在神經網路中被廣泛使用的激活函數。它的數學公式如下圖: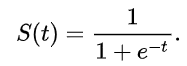

它可以說是神經網路界的老前輩。
它的特色就是:無論你丟進去多大的數字，
它最後都會 把結果壓縮到 0 和 1 之間 。

這樣的特性非常適合用來做「機率」的解釋。
舉例來說，如果我要判斷一封信是不是垃圾郵件，
輸出 0.9 就代表 「有 90% 的可能是垃圾信」，
輸出 0.1 就代表 「只有 10% 的可能」。

但 Sigmoid 也有它的缺點，
因為它在數值很大或很小的時候，輸出幾乎固定在 0 或 1，
這會讓網路學習變得很慢。( 梯度消失 (gradient vanishing) 問題 )(註)
這就是為什麼它後來慢慢被其他激活函數取代。

註 : 梯度消失問題 ：

當我們在訓練深層神經網路時，
需要透過 「誤差反向傳播」（Backpropagation） 來更新權重。
這個過程中會不斷計算「梯度」（就像是往哪個方向走才會更接近答案的指南）。

但如果用到像 Sigmoid 這類會把數字
壓縮到 0 和 1 之間的函數，問題就出現了：
當輸入數字非常大或非常小時，
Sigmoid 的輸出幾乎不會再變動（變化趨近平坦）。
這代表梯度會變得非常接近 0。

一旦梯度接近 0，誤差就無法順利往前傳遞，前面的層幾乎學不到東西。

簡單一點來說，梯度消失就像是神經網路學習的訊號在傳遞過程中慢慢變小，
最後消失不見，導致網路越深，前面的神經元就越「學不動」。

參考資料:
https://medium.com/@adea820616/activation-functions-sigmoid-relu-tahn-20e3ae726ae
https://zh.wikipedia.org/zh-tw/S%E5%9E%8B%E5%87%BD%E6%95%B0
https://qifong04.medium.com/%E9%97%9C%E6%96%BC%E6%A2%AF%E5%BA%A6%E6%B6%88%E5%A4%B1%E8%88%87%E6%A2%AF%E5%BA%A6%E7%88%86%E7%82%B8-287f4e039633

ReLU：簡單卻超實用

接著是 ReLU，
它的名字聽起來很學術，Rectified Linear Unit，但規則其實非常簡單：

-如果輸入是負數 → 直接輸出 0。
-如果輸入是正數 → 原封不動輸出。

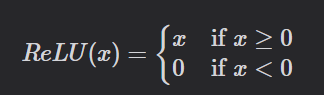
可以把他比喻成過濾器，所有負數都被它過濾掉，只有正數能通過。
就是這麼簡單的規則，卻可以讓網路的學習速度大大提升，
因為它避免了 Sigmoid 常常遇到的 「梯度消失」 問題。

而在實務上，ReLU 則幾乎是「隱藏層」的標準配備。
它像是樸實無華的工具，
沒什麼華麗的數學公式，但卻簡單有效，讓神經網路能跑得快又準。

但它也不是沒有缺點，
其可能會有 Dead ReLU Problem（由於負數部分恆為零，會導致一些神經元無法激活）。
但除此之外，它確實是一個很好用的「過濾器」。

參考資料:
https://hackmd.io/@sysprog/constant-time-relu

Softmax 函數 : 讓機率說話

Softmax 和前面兩個有點不一樣，它通常用在 「多分類問題的輸出層」。
它的公式看起來有點複雜，
但我們簡單來說，它就是會把一堆數字轉換成
一組 「加總為 1 的機率分佈」。

假設我們要辨識手寫數字 0~9，輸入一張數字的影像後，經由 Softmax 回歸，
最後將會輸出該影像屬於 0 ~ 9 個別的機率為何，且其個別的機率總和為 1。

如果還聽不懂的話，不妨看看以下範例:

[2.3, 1.1, 0.1, 4.7, 3.3, 0.8, 2.9, 1.0, 0.5, 0.3]

這些數字你第一眼看可能看不出個所以然，但若是經過 Softmax 轉換呢?

[0.05, 0.02, 0.01, 0.60, 0.20, 0.03, 0.07, 0.01, 0.005, 0.005]

這樣就比較清楚了：
這個模型認為這張圖有 ** 「60% 的機率是數字 3」，
而有 ** 「20% 的機率是數字 4】。

Softmax 的特色就是：

-適合多分類問題
-每個輸出值都可以直接解釋成「機率」
-幫助我們快速做決策（挑選機率最高的那一類）

總結大比較:表格時間

如果你還是看文字看到頭很痛的話，
我這邊也用AI協助我生成了一份比較表格，
路過不妨再複習一次: