Deep Convolutional Generative Adversarial Network 簡稱 DCGAN 中文稱作深度卷積對抗式生成網路,原始的論文連結.這是基於 GAN 上所做的工作.
跟 GAN 不同的是,DCGAN 把 convolution 引進網路結構中.在 discriminator 中輸入的圖像會經過層層 convolution 之後變成一個預測是否為真實圖片的機率;在 generator 中會把輸入的 z 向量經過層層 deconvolution 輸出生成式的圖片.可以看到它的結構如下圖.
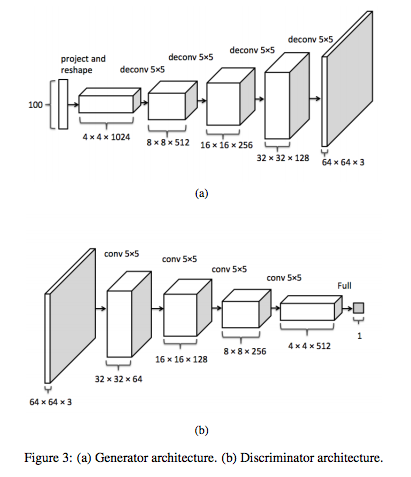
(圖片出處論文)
同時論文中有提到許多如何訓練一個穩定 GAN 的細節,但這裡只先單純的把 convolution 以及 deconvolution 實現進 GAN,以下會使用 MNIST 手寫數字資料集來嘗試訓練一個 DCGAN.
batch_size = 256
g_dim = 100
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 2, 2, 1], padding = 'SAME')
def deconv2d(x, W, output_shape):
return tf.nn.conv2d_transpose(x, W, output_shape, strides = [1, 2, 2, 1], padding = 'SAME')
這裡我們會建立生成式網路 (generator) 以及判斷式網路 (discriminator)
在 discriminator 中,首先會輸入一個 None x 784 維的 MNIST 資料,首先會先把它變成一個二維的圖片向量也就是 None x 28(width) x 28(height) x 1(channels).接下來就是連續的使用 filter 作 convolution,其中 strides = 2,使得每做完一次 convolution 的輸出長和寬就會變成一半.以下是輸入圖片的維度變化順序:
在 generator 中,首先會輸入一個 None x 128 維從 noise 中取樣出的向量,首先經過一個全連結會把它擴展成 None x 4*4*64,再把它 reshape 成一個 None x 4(width) x 4(height) x 64(channels) 的輸入(可以想像成把輸入向量變成一個 4x4 的圖像).接下來就是經過一連串的 deconvolution,最後輸出圖片.以下是輸入的維度變化順序:
x_d = tf.placeholder(tf.float32, shape = [None, 784])
x_g = tf.placeholder(tf.float32, shape = [None, g_dim])
weights = {
"w_d1" : weight_variable([5, 5, 1, 32], "w_d1"),
"w_d2" : weight_variable([5, 5, 32, 64], "w_d2"),
"w_d3" : weight_variable([7 * 7 * 64, 1], "w_d3"),
"w_g1" : weight_variable([g_dim, 4 * 4 * 64], "w_g1"),
"w_g2" : weight_variable([5, 5, 32, 64], "w_g2"),
"w_g3" : weight_variable([5, 5, 16, 32], "w_g3"),
"w_g4" : weight_variable([5, 5, 1, 16], "w_g4")
}
biases = {
"b_d1" : bias_variable([32], "b_d1"),
"b_d2" : bias_variable([64], "b_d2"),
"b_d3" : bias_variable([1], "b_d3"),
"b_g1" : bias_variable([4 * 4 * 64], "b_g1"),
"b_g2" : bias_variable([32], "b_g2"),
"b_g3" : bias_variable([16], "b_g3"),
"b_g4" : bias_variable([1], "b_g4"),
}
var_d = [weights["w_d1"], weights["w_d2"], weights["w_d3"], biases["b_d1"], biases["b_d2"], biases["b_d3"]]
var_g = [weights["w_g1"], weights["w_g2"],weights["w_g3"], weights["w_g4"], biases["b_g1"], biases["b_g2"],biases["b_g3"], biases["b_g4"]]
def generator(z):
#100 x 1
h_g1 = tf.nn.relu(tf.add(tf.matmul(z, weights["w_g1"]), biases["b_g1"]))
#-1 x 4*4*128
h_g1_reshape = tf.reshape(h_g1, [-1, 4, 4, 64])
output_shape_g2 = tf.stack([tf.shape(z)[0], 7, 7, 32])
h_g2 = tf.nn.relu(tf.add(deconv2d(h_g1_reshape, weights["w_g2"], output_shape_g2), biases["b_g2"]))
output_shape_g3 = tf.stack([tf.shape(z)[0], 14, 14, 16])
h_g3 = tf.nn.relu(tf.add(deconv2d(h_g2, weights["w_g3"], output_shape_g3), biases["b_g3"]))
output_shape_g4 = tf.stack([tf.shape(z)[0], 28, 28, 1])
h_g4 = tf.nn.tanh(tf.add(deconv2d(h_g3, weights["w_g4"], output_shape_g4), biases["b_g4"]))
return h_g4
def discriminator(x):
x_reshape = tf.reshape(x, [-1, 28, 28, 1])
# 28 x 28 x 1
h_d1 = tf.nn.relu(tf.add(conv2d(x_reshape, weights["w_d1"]), biases["b_d1"]))
# 14 x 14 x 32
h_d2 = tf.nn.relu(tf.add(conv2d(h_d1, weights["w_d2"]), biases["b_d2"]))
# 7 x 7 x 64
h_d2_reshape = tf.reshape(h_d2, [-1, 7 * 7 * 64])
h_d3 = tf.nn.sigmoid(tf.add(tf.matmul(h_d2_reshape, weights["w_d3"]), biases["b_d3"]))
return h_d3
def sample_Z(m, n):
return np.random.uniform(-1., 1., size=[m, n])
g_sample = generator(x_g)
d_real= discriminator(x_d)
d_fake = discriminator(g_sample)
d_loss = -tf.reduce_mean(tf.log(d_real) + tf.log(1. - d_fake))
g_loss = -tf.reduce_mean(tf.log(d_fake))
# 只更新 discriminator
d_optimizer = tf.train.AdamOptimizer(0.0001).minimize(d_loss, var_list= var_d)
# 只更新 generator parameters
g_optimizer = tf.train.AdamOptimizer(0.0001).minimize(g_loss, var_list= var_g)
step 0, discriminator loss 2.41063 generator loss 0.29276
step 100, discriminator loss 0.85784 generator loss 1.39115
step 200, discriminator loss 0.44820 generator loss 2.21131
step 300, discriminator loss 0.84276 generator loss 1.69659
step 400, discriminator loss 0.72615 generator loss 1.95878
step 500, discriminator loss 0.71053 generator loss 1.77434
step 600, discriminator loss 0.71514 generator loss 1.84341
step 700, discriminator loss 0.51880 generator loss 1.86431
step 800, discriminator loss 0.26334 generator loss 2.29687
step 900, discriminator loss 0.22319 generator loss 2.62868
step 1000, discriminator loss 0.18192 generator loss 2.64233
step 2000, discriminator loss 0.24685 generator loss 2.95130
step 3000, discriminator loss 0.05564 generator loss 4.25037
step 4000, discriminator loss 0.04217 generator loss 4.71265
step 5000, discriminator loss 0.22856 generator loss 3.57268
step 6000, discriminator loss 0.12961 generator loss 4.49799
step 7000, discriminator loss 0.04830 generator loss 5.12374
step 8000, discriminator loss 0.01379 generator loss 6.38079
step 9000, discriminator loss 0.00626 generator loss 5.92065
step 10000, discriminator loss 0.05310 generator loss 6.42939
step 11000, discriminator loss 0.01101 generator loss 7.24146
step 12000, discriminator loss 0.00744 generator loss 6.53067
step 13000, discriminator loss 0.01497 generator loss 8.72534
step 14000, discriminator loss 0.05123 generator loss 5.25377
step 15000, discriminator loss 0.00633 generator loss 6.64243
step 16000, discriminator loss 0.00066 generator loss 7.72938
step 17000, discriminator loss 0.00209 generator loss 7.22791
step 18000, discriminator loss 0.00046 generator loss 7.68677
step 19000, discriminator loss 0.00222 generator loss 6.73453
step 20000, discriminator loss 0.00914 generator loss 5.61193
以下是連續 gif 圖,這一連串的訓練時間真的是還滿久的...很有趣的有兩點

我們實作了 DCGAN ,以及利用 MNIST 資料來測試它的效果.
效果跟預期有些差異,其中只出現了某一數字,然後在某一時刻生成器發生崩壞.
