我在學習ARIMA時間序列模型的時候就有一個疑問，我們要自己去找尋變數d,p,q，我知道這是個學習過程，通過自己手動操作尋找，更能體會acf，pacf，分差這些概念，我也很認真地去讀了，但我發現其實在R語言當中，有一個可以直接尋找最小AICc值的code，的確讓我耳目一新，AIC跟AICc有點像R^2與Adjust R^2，是用來評估模型的。

在進行運算的時候，我先將最後12筆資料(一年)拉出來，方便預測後進行測試

newdata_t = newdata[1:(length(newdata)-12)]

newdata_t = ts(newdata_t,frequency =  12,start = c(2005,1))

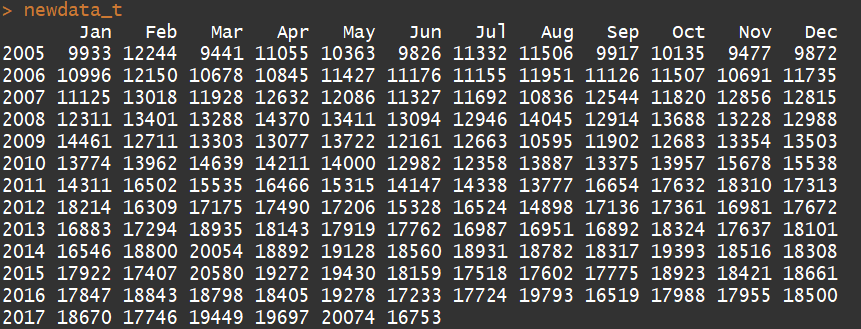
q = forecast(newdata_t,h = 20)

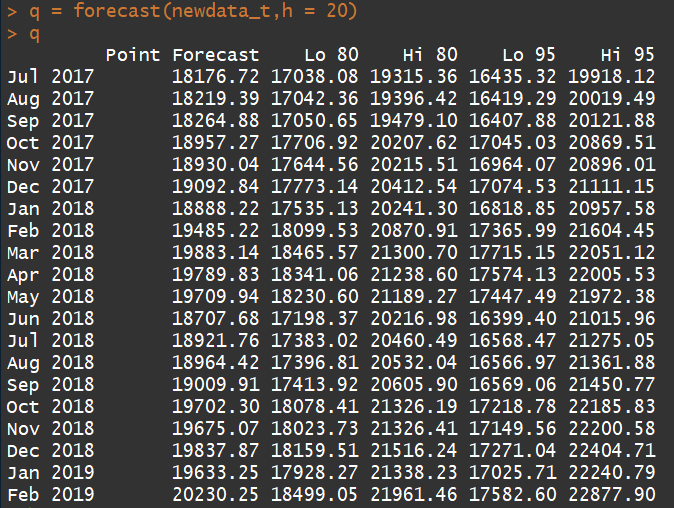
plot.forecast(q)

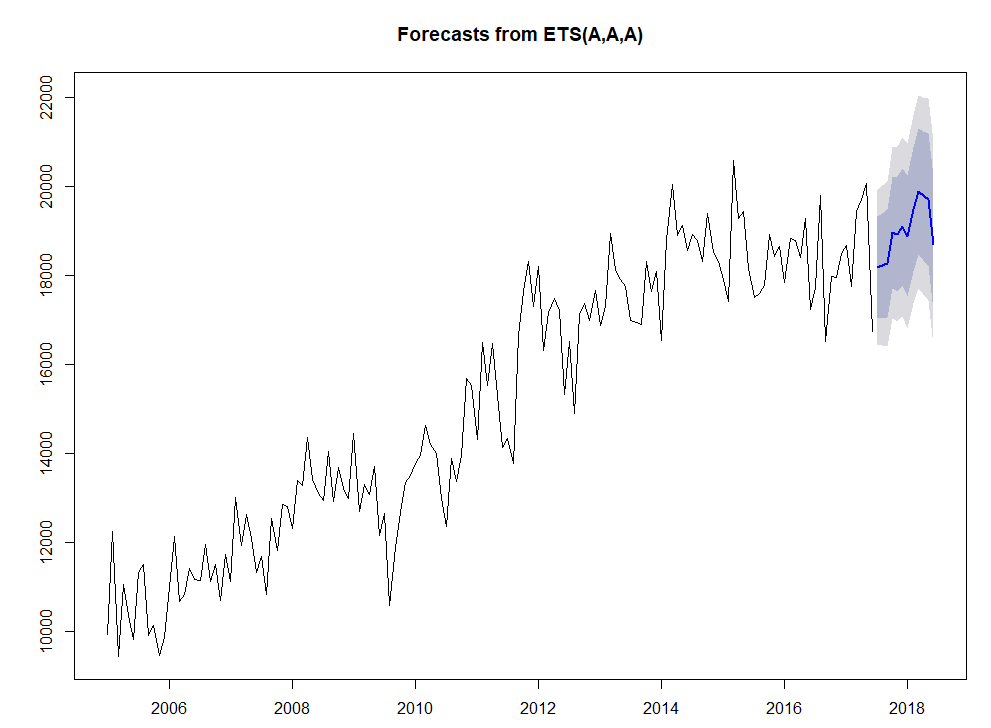
arima1<-auto.arima(newdata_t,trace=T)

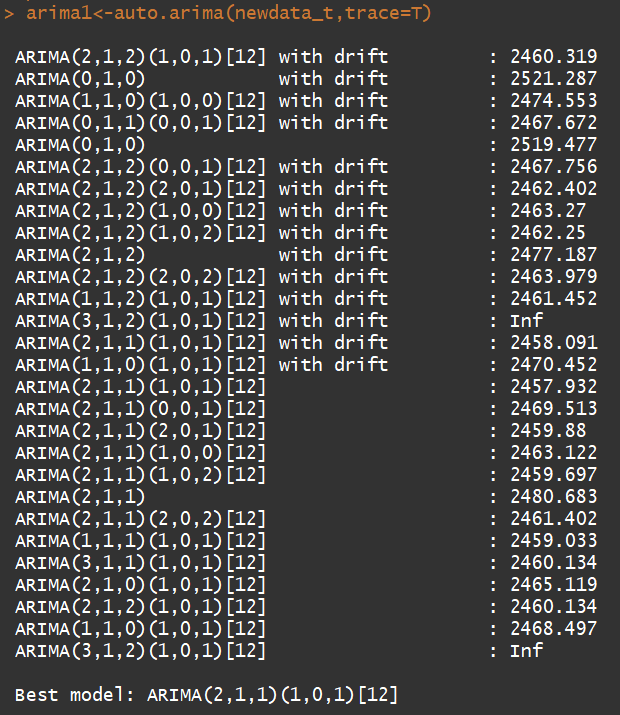
plot(forecast(Arima(newdata_t,order=c(2,1,1),seasonal=c(1,0,1)),h=12))

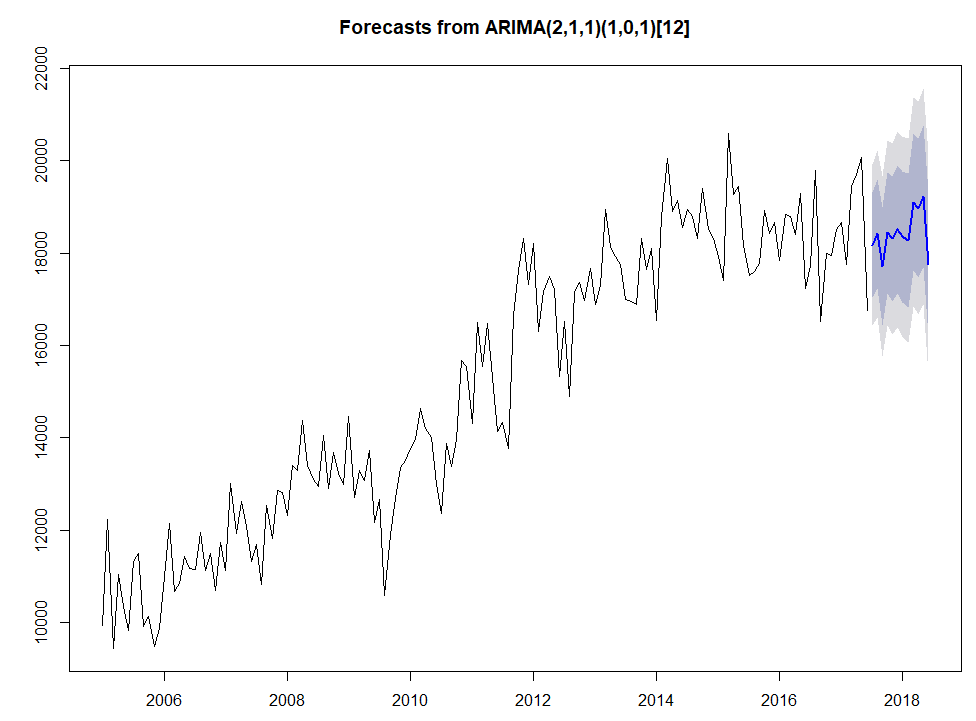
兩種方法，預測出了兩種結果，應該要有一種方法可以去判斷哪個比較準才對，載時間序列模型當中，AICc已告訴我模型適合一定是下面的模型更好，但我要想想看怎樣才能拿實際數字去驗證看看是不是真的如此。

*補充：
AIC
Akaike 資訊準則。較小值表示較佳的模型。只有在兩個模型有接近相等的觀測數目時，才應比較 AIC 值。AIC 值可變成負數。AIC 是以回應變數的真實分配與模型指定的分配之差異的 Kullback-Leibler 資訊量值為基準。
AICC
已更正的 Akaike 資訊準則。此版本的 AIC 會調整此值以考量比較小的樣本大小。結果是額外效果會懲罰 AICC (超過 AIC)。隨著樣本大小增加，AICC 和 AIC 都會收斂。
4. BIC
貝氏資訊準則 (BIC) (也稱為 Schwarz 貝氏準則 (SBC)) 是模型殘差平方和與效果數目的遞增函數。回應變數中的不明變異和效果數目會使 BIC 值提高。因此，較低的 BIC 意指較少的解釋變數、配適更佳或兩者。BIC 會懲罰可用參數 (比 AIC 更強烈)。