前言

上一篇講了一堆安裝的困難，如果，本機安裝不起來，可以直接使用Google Colaboratory 雲端環境，它有免費的GPU/TPU 可使用，而且常用套件都已安裝好了，Enable的程序很簡單，有興趣的讀者可參考 【Google Colab Free GPU Tutorial】 一文，照圖操作即可。

接下來，我們就從深度學習套件的主要功能說起。

為什麼需要深度學習的套件?

深度學習套件的主要功能，個人認為有兩項：

1. 自動微分(Automatic Differentiation)
2. 各式神經層(Layer)的實踐

【梯度下降】(Gradient Descent)是神經網路(Neural Network)優化求解的主流方法，以下圖為例，我們可以將神經網路看作是多條迴歸線的組合，例如，紅粗線所示就是一條迴歸線，y = w0 + w1 * x1 + w2 * x2 + w3 * x3，【梯度下降】的目標依據X/y的訓練資料，對權重(Wi)求解：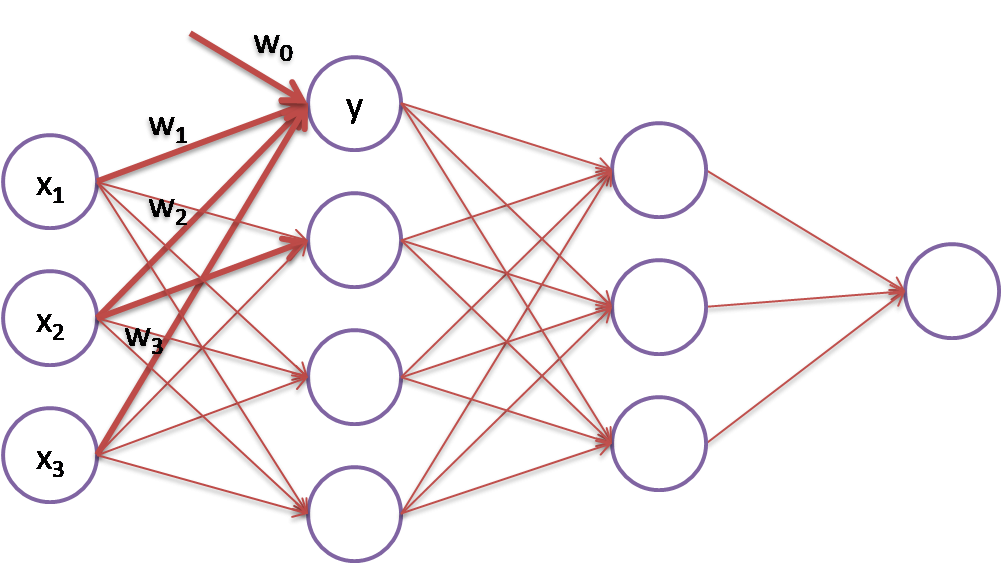

圖一. 多層神經網路(Neural Network)

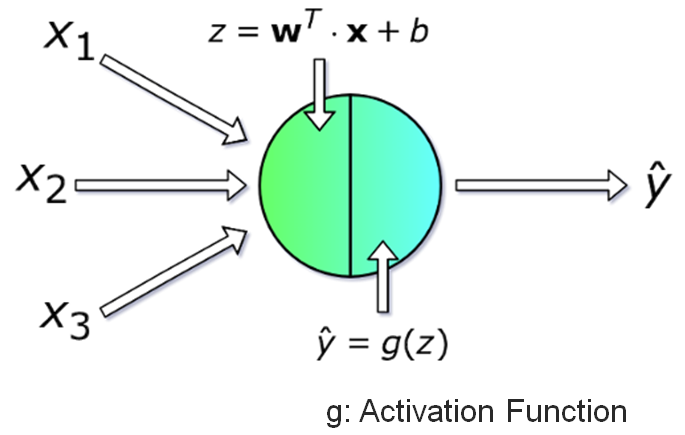
圖二. 一個神經元的計算就是一條迴歸線

神經網路是多條迴歸線的組合，每一條可能又加上 【Activation function】，要以純數學推導出模型公式應該非常困難，因此，專家學者利用【梯度下降】逼近法找出最佳解，它是【正向傳導】(Forward Propagation)與【反向傳導】(Backpropagation)不斷迭代(Iteration)的過程。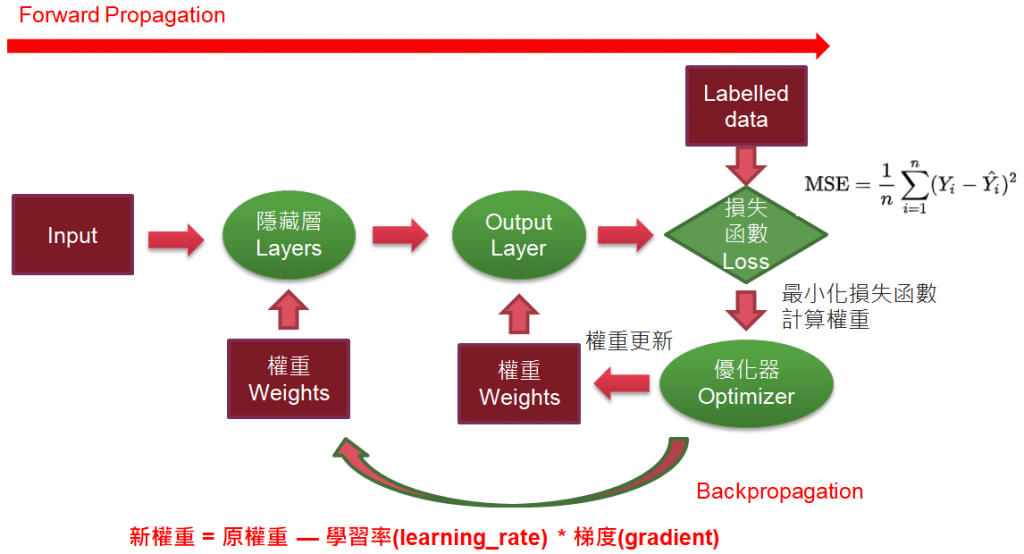

圖三. 【梯度下降】(Gradient Descent)

正向傳導：

1. 一開始Wi設為任意值，已知xi，就可以求得yi。
2. 同理，可以算完同一層的其他迴歸線的yi。
3. 下一層又以上一層的yi為輸入，計算下一層的神經元。
4. 經過層層的計算，最後可以算出預測值，進而求出損失函數，例如均方誤差(MSE)，公式如圖三所示。

反向傳導：

1. 根據損失函數，計算梯度(Gradient)，通常就是一階導數，即對Xi的偏微分。
2. 再參照下面的公式，更新所有迴歸線的權重:
   新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)
3. 再回到正向傳導，依據新權重，求算預測值。

如此交互運算，直至迭代的損失函數值不再變動時為止，這時候的權重(Wi)就被認為最佳解。詳細的說明可參考【Day N+1：進一步理解『梯度下降』(Gradient Descent)】。

以下，我們就來看看程式如何作梯度下降。

程式碼

不論 Tensorflow 或 PyTorch 等深度學習套件，他們都提供自動微分的功能，也就是說，我們宣告了網路架構及損失函數的定義，Tensorflow/PyTorch 就會自動幫我們作反向傳導，求算梯度。例如以下程式：

import numpy as np 
import tensorflow as tf 

# x 宣告為 tf.constant，就要加 g.watch(x)
x = tf.Variable(3.0)

# 自動微分
with tf.GradientTape() as g:
    #g.watch(x)
    y = x * x
    
# g.gradient(y, x) 取得梯度
dy_dx = g.gradient(y, x) # Will compute to 6.0

# 轉換為 NumPy array 格式，方便顯示
print(dy_dx.numpy())

定義 y = x * x，y 對 x 偏微分就等於 2 * x，當 x = 3時，梯度就等於 2*3 = 6。
看起來很簡單，我們不需要套件，可以自己算，但若是加上activation function，而且是多層網路，那就困難了，所以深度學習套件還是可以幫我們很大的忙。

注意，當 x 宣告為 tf.Variable，預設會參與梯度下降的訓練，相對的，若x宣告為 tf.constant，就不會參與梯度下降的訓練，除非我們加上 g.watch(x)，這跟 1.x 版的 x.initializer.run() 或 sess.run(x.initializer) 是一樣的意思。

PyTorch 範例

順便看一下 PyTorch 寫法。

import torch

x = torch.tensor(3.0, requires_grad=True)
y=x*x

# 反向傳導
y.backward()

print(x.grad)

以上程式的檔案名稱為 02_02_tf_linear_regression.ipynb。

簡單迴歸範例

檔案名稱為 02_02_tf_linear_regression.ipynb。

import numpy as np 
import tensorflow as tf 

# y_pred = W*X + b
W = tf.Variable(0.0)
b = tf.Variable(0.0)

# 定義損失函數
def loss(y, y_pred):
    return tf.reduce_mean(tf.square(y - y_pred))

# 定義預測值
def predict(X):
    return W * X + b
    
# 定義訓練函數
def train(X, y, epochs=40, lr=0.0001):
    current_loss=0
    # 執行訓練
    for epoch in range(epochs):
        with tf.GradientTape() as t:
            t.watch(tf.constant(X))
            current_loss = loss(y, predict(X))

        # 取得 W, b 個別的梯度
        dW, db = t.gradient(current_loss, [W, b])
        
        # 更新權重
        # 新權重 = 原權重 — 學習率(learning_rate) * 梯度(gradient)
        W.assign_sub(lr * dW) # W -= lr * dW
        b.assign_sub(lr * db)

        # 顯示每一訓練週期的損失函數
        print(f'Epoch {epoch}: Loss: {current_loss.numpy()}') 


# 產生隨機資料
# random linear data: 100 between 0-50
n = 100
X = np.linspace(0, 50, n) 
y = np.linspace(0, 50, n) 
  
# Adding noise to the random linear data 
X += np.random.uniform(-10, 10, n) 
y += np.random.uniform(-10, 10, n) 

# reset W,b
W = tf.Variable(0.0)
b = tf.Variable(0.0)

# 執行訓練
train(X, y)

# W、b 的最佳解
print(W.numpy(), b.numpy())

import matplotlib.pyplot as plt 

plt.scatter(X, y, label='data')
plt.plot(X, predict(X), 'r-', label='predicted')
plt.legend()

結果如下：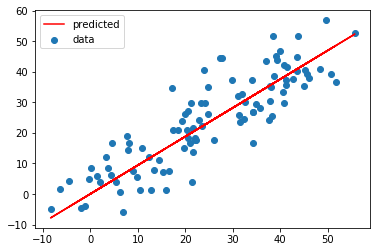

結論

以上雖無關Keras語法，不過，筆者認為梯度下降的基本觀念很重要，就整理一下，希望有助於初學者。
下一篇，我們將介紹一支完整的 Keras 程式，說明神經層(Layer)，Happy coding。

本篇範例包括 02_01_tf_gradient.ipynb、02_02_tf_linear_regression.ipynb，可自【這裡】下載。