你是說...樹嗎?

嘿~丟！鐵人賽至今已經過半，實在是油盡燈枯，想不到主題了，剛好看到這兩個很讚的樹，覺得很適合這次的主題！加上筆者我又對大自然的碎形相當著迷，接下來的遊戲就拿種樹來做收集養成的要素吧，也該是時候拿第二章聊過的物件來實作了！
https://openprocessing.org/sketch/90192
https://openprocessing.org/sketch/1009781

剛剛洗澡時我稍微構思了一番如何設計，接著讀一下人家的程式碼，欸！果然邏輯大同小異，來幫萌新們入門一下，這個所謂的遞迴函式在我國中時可是搞死我了，當時不善於溝通的我，在準備程式競賽時遇到了一個題目開始學習用遞迴函式，卻不斷寫錯造成無窮迴圈，花了五個中午耗時無果，就被電腦老師以為我在偷懶，沒寫半個題目，被罵了個臭頭，今天，就讓我們拆分成好幾個步驟，以循序漸進的方式打敗這個大魔王吧！

何謂遞迴

簡單來說就是，重複的事情一直做，比方說田徑校隊今天要徵選，共有10人參加，教練說要考驗大家的耐力，因此要進行5輪的3000公尺長跑，每一輪會淘汰1人，最後剩下5人入圍。

如果要用程式做出這樣的競賽（可以想像成google的奧運遊戲），剛開始寫程式的人，可能就會很直接地想，那我就準備五個比賽，每次淘汰一人即可，先不說這樣要寫多久，如果今年報名人數突然暴漲，共有20~30人不等，人數不確定，那怎麼只淘汰到剩五人呢？（也先不說教練有多變態讓大家跑3000公尺數十次）

其實答案很簡單，就是把重複的最小基本單位給定義出來，在這個例子中就是每一輪的比賽，設計的關鍵是每次的輸入人數都不同，讓人數持續減少，因此，也許你已經看過這樣的寫法：

let people = 10; // 輸入10人
race(people);
function race(N){
    // 進行一輪淘汰賽
    N--;
    if(N > 5) race(N);
    else alert('共有' + N + '人入圍') // 輸出5人
}

遞迴存在的意義

不過如果僅僅只是這樣，肯定會被質疑，用for迴圈或是while迴圈不是一樣能完美解決嗎？是的，如果問題的確那麼單純，進一步想，假設今天教練希望分別招募一隊和二隊，因此在每一場比賽後將所有人分成AB兩組，不淘汰，而讓AB兩組再分別做競爭，繼續分成A-1、A-2、B-1、B-2組，而且每一個組別根據人數不同，有不同的賽式，如果僅剩3人以下，則以1000公尺競速取勝，剩4人則進行2對2的對抗大隊接力，剩5人以上則繼續採用3000公尺，那麼事情就不單純了。

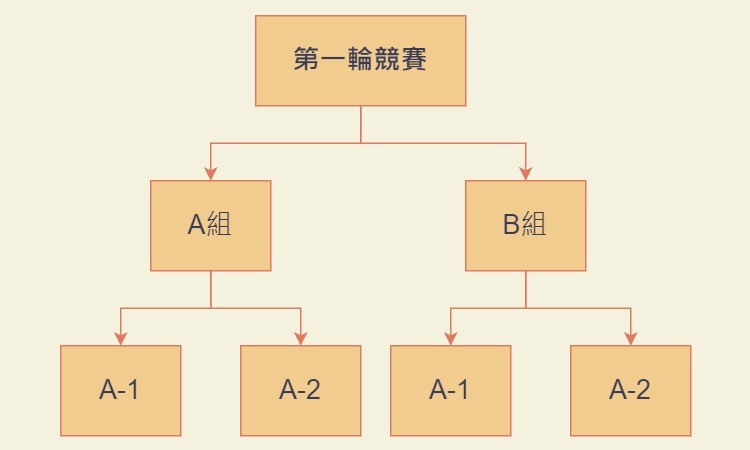
其實這就是樹狀圖的概念，但是要用一般的迴圈實現，會遇到的第一個問題就是，那到底有幾場比賽需要進行？答案也很單純：比了才會知道！因此如果有一個函式，能幫我們在比賽進行的當下，依據目前剩下的人數，判斷應該採用甲乙丙三種賽事中哪一種，然後在每一個次進行比賽後，分割好兩組，並且重複呼叫該函式，就能達到事半功倍的效果了。

樹狀圖

讓我們回到畫一棵樹的主題，前面基於現實的比喻或許還是過於抽象，讓我們從一棵樹的基本單位開始：樹枝，搭配第二章學到的物件，我們可以開始設計一個樹枝，它有三個完整的部件：

1. 樹枝本身
2. 有父節點（靠近根部）
3. 有子節點（靠近葉子）

先從一個最簡單易懂的代碼來做演示：如果樹枝完全沒有分支

let Tree = function(x, y, times){
    // 樹枝本身(的屬性)
    this.startX = x;
    this.startY = y;
    this.vectorX = 0;
    this.vectorY = -10; // 每一節只有10像素，並且只會向正上方成長
    
    // 根據輸入條件判斷是否創建新的樹枝
    if(times > 0){
        let endX = x + this.vectorX;
        let endY = y + this.vectorY;
        this.son = new Tree(x + vectorX, y + vectorY, times - 1);
    }
    else{
        alert("too many isn't it?"); // 在樹枝的最末稍停止遞迴時，會觸發
    }
};
let justAVar = new Tree(10, 10, 100);

其實就跟最一開始舉例的3000公尺淘汰賽一樣單純

不過，我們已經透過物件的型式，相當妥善的把每一節樹枝接起來了，把以上整段代碼貼上console就會看到如下的畫面，去點開每一個樹枝，都會看到裡面又有它的子樹枝，一環接一環：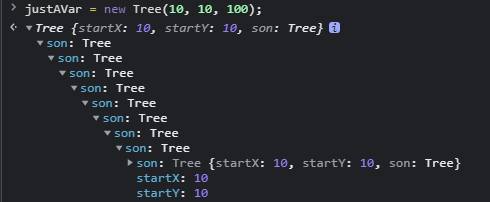

接著我們就可以進一步設計，讓每一個樹枝都會進行分岔，成為兩個長度各只有一半的子樹枝，角度分別設定正負30度，並且計算每一樹枝的末梢位置endX、endY，用來連結子樹枝的起始點startX、startY：

let Tree = function(father, x, y, r, theta, times){
    this.father = father;
    this.startX = x;
    this.startY = y;
    this.r = r;
    this.theta = theta;
    if(times > 0){
        let endX = x + r * Math.cos(theta / 180 * Math.PI);
        let endY = y + r * Math.sin(theta / 180 * Math.PI);
        this.son = [new Tree(this, endX, endY, r / 2, theta - 30, times - 1),
                    new Tree(this, endX, endY, r / 2, theta + 30, times - 1)];
    }
    else{
        // 如果要讓末端開花結果，就寫在這
    }

    this.Draw = function(x = this.startX, y = this.startY,
                         r = this.r, theta = this.theta){
        context.beginPath();
        context.moveTo(x, y);
        context.lineTo(x + r * Math.cos(theta / 180 * Math.PI),
                       y + r * Math.sin(theta / 180 * Math.PI));
        context.lineWidth = 1 + r/50;
        context.strokeStyle = 'rgba(179, 198, 213, 1)';
        context.stroke();
        // 如果有子樹枝，就繼續呼叫所有的子樹枝
        if(this.son) this.son.forEach(branch => branch.Draw()); // 遞迴
    };
};

接著將物件實例化：
myTree = new Tree(window, WIDTH/2, HEIGHT, HEIGHT/4, -90, 10);

在我們準備好動畫框架處寫上該物件的繪圖方法 myTree.draw()，可以和上面的建構式做對照，這也是屬於一個遞迴函式：

function Redraw(){
    Clear(context);
    myTree.draw();
}

如此一來就能很輕鬆地畫出這顆樹了呢！

摁?你說它長得有點醜嗎，確實，畢竟，這不是一顆真正的樹，明天我們再來美化吧！

順帶一提，可以透過改變角度和長度的比例（上面的例子是30度和1/2），來達到不一樣的效果：

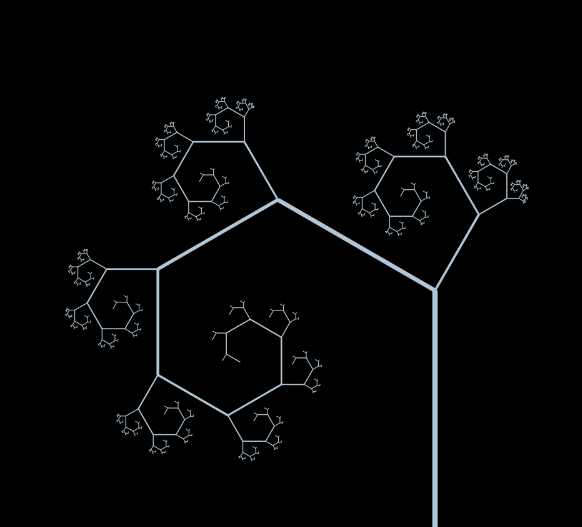
有沒有曾經在哪裡看過很眼熟呢？這個就叫做碎形（又是一個大坑），像是雪花就是典型的碎形了，其不僅呈現出大自然之美，也有著許多值得討論的地方，有興趣的朋友可以去找碎形的影片來看，這次系列文就不著墨了！

demo 明天再補上吧！早點睡休息重要

後記

再累還是要後記，原本想用Branch(分支)來命名的，結果腦子一昏就寫成Tree(樹)，整個很奇怪呀~~怎麼這棵樹是由一堆樹組成的呢？後來想想算了懶得改了哈哈，說不定Branch是個生詞很多人看不懂（自我安慰）。