今天摘要的段落是可以「跟著做」的練習，我覺得今天的段落超有趣的！！！

前情提要

今天內容是【CH5. 校準的估算：你目前所知有多少？】的前半，延續昨天的進度，在真正進行衡量之前，需要思考的議題有：

1. 這項衡量要支援什麼決策？
2. 要衡量的事物，若用可觀察到的結果來定義，會是什麼？
3. 這個事物如何影響相關決策？
4. 關於這項衡量，你目前所知有多少？（也就是，目前的不確定程度為何？）
5. 額外資訊的價值為何？

在本章中，作者討論的是第 4 題。目標是「瞭解你已經知道的事」，說得更具體一點，是學會用「量化的表達方法」，來表達自己「已經知道的事」。

在上章 IT 防護的例子裡，我們看到專家對病毒攻擊影響做出了數量的估算（昨天的最後一張圖），作者表示，「有 90% 的機會，真實的數值會落在專家給定的上下區間內」。而本章就在討論，為什麼當專家說有 90% 機會時，就是 90% 會正確。

表達不確定性的方法

剛才說的「表達目前知道什麼」，其實是指「表達不確定性」（註：不確定性=一種以上的可能）

表達方式有：

• 範圍：例如 1000～2000。
  • 這個範圍有一定機會可以包住正確答案。這個機會稱為「信賴區間 (confidence interval, CI)」，例如上文 IT 專家的信心是 90% CI。
• 是否 & 機率：例如 70% 機率客戶會成交 or 70% 機率不會成交。

過度自信

接下來作者表示，沒有經過「校準訓練」過的人，靠經驗或直覺給出範圍或機率時，絕大多數人都有「過度自信」的情況。（反之則為信心不足，但絕大多數人是過度自信）

也就是，當我們要求 90% CI 的估算時，正確答案落在區間的次數少於 90%。

接下來作者介紹校準這種「過度自信」狀況的方法！這個環節很有趣！強烈建議跟著做！

校準練習

接下來作者會給出 10 個題目，讓讀者可以嘗試寫出範圍 & 機率。寫完後會有一連串的引導，來讓讀者體會「為什麼你估出的數字是過度自信的」，以及校準的方法。

作者真正的校準研習營中，他會給出更多的題目，用至少半天的時間來進行校準練習，真正建立思考的習慣。而在書中只提供了 10 個題目，作者表示：對未經訓練的人，光是 10 個題目就可以看出很明顯的傾向。

1. 範圍練習：目標 90% CI

首先是範圍類的練習，目標是達到 90% CI，也就是等下對答案時，10 題要有 9 題是命中的。

提醒：

• 不要查詢任何資料，把注意力放在「你現在已知的資訊（或看法）」
• 範圍要夠大，以達成 90% CI

題目如下，請寫出範圍的上限與下限：

1. 1938 年英國蒸汽火車頭以多快的速度創下新的速度紀錄（英哩/小時）
2. 牛頓爵士在哪一年發表萬有引力定律
3. 一般商務名片長度為多少英吋
4. 網際網路 (當時叫 Arpanet) 是在哪一年建立做為軍方的通訊系統？
5. 莎士比亞出生於哪一年
6. 紐約到洛杉磯之間的飛行距離是多少英哩？
7. 一個圓形佔據等寬正方形面積的比例？
8. 卓別林於幾歲時去世？
9. 這本書第一版的重要為幾英磅？
10. 電視影集《夢幻島》(Gilligan's Island) 第一次播出的日期

2. 是否練習

接著要針對每項敘述選擇「是/否」，然後圈出一個「機率」來反映你對答案的信心程度，通常情況是：

• 你完全確定你的答案，則機率是 100%
• 若你毫無概念，機率等同於擲硬幣，也就是 50%

等等在練習時，直接從 50%, 60%, 70%, 80%, 90%, 100% 之間選一個就好了。

敘述：

1. 古羅馬人是被古希臘人征服的
2. 世界上沒有三峰駱駝
3. 1 加侖的汽油比 1 加侖的水重量輕
4. 火星到地球的距離永遠大於金星到地球的距離
5. 波士頓紅襪隊贏得第一屆世界大賽
6. 拿破崙出生於科西嘉島
7. M 是英文中最常用到的三個字母之一
8. 2002 年桌上型電腦平均的購買價格低於 1500 美元
9. 詹森在當副總統之前是州長
10. 1 公斤比 1 英磅重

測驗：你的估算是否為 90% CI

在對答案之前，要來衡量剛才的估算是否為 90% CI。

作者從題目中選出其中一個，「牛頓爵士在哪一年發表萬有引力定律」來做實驗。

A. 如果對答案之後，你命中了牛頓的書籍出版日，你可以獲得 1000 美元

B. 去玩一個轉盤遊戲（如下圖），如果轉盤停在 90% 的區間，你可以贏得 1000 美元。

你會選哪一個？

作者將此實驗稱為「相等賭局測試 (equivalent bet test)」，

• 在實驗中，絕大多數人會選擇轉盤遊戲，
• 這代表你認為輪盤的機會更高
• 也就是說，剛才的估算，不是真正的 90% CI（可能是 50% CI，總之低於 90%）
• 你表達出來的不確定程度，低於真正的不確定性

對答案

接下來可以對個答案，來看看命中率。

btw 我在書上發現了 2014 年的練習紀錄，因為是過去的事了，所以我就不帶羞恥地分享出來。

評估結果

• 範圍題的正確題數
  • 少於 7 個 - 過度自信
  • 少於 5 個 - 非常過度自信
• 是非題
  • 把每一題圈選的機率轉成小數，例如 0.5, 0.6...
  • 然後加總，例如 7.9，這代表你預期答對 7.9 題
  • 和答對的題數相信，若比預期答對題數少 2.5，仍可能是過度自信

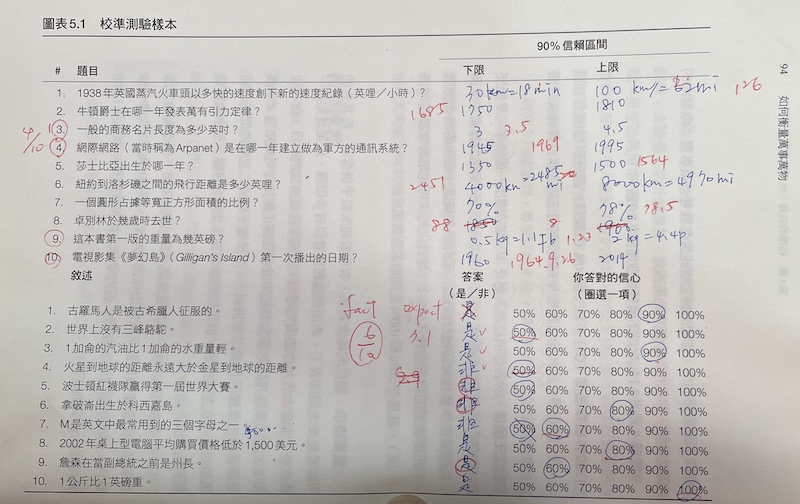
作者表示：整體來說人們在是非題的表現會比範圍題好，但通常在訓練前，一致有過度自信的情況。作者的統計在是非題型裡，平均預期 74% 答對，而真實情況是 62% 。

至於範圍題，會有超過 56% 的人表現非常非常差，不過真正「尺度準確的人」，只有 1/ 612 的錯誤機率。

改善手法

本章的後半，作者介紹了他在「校準訓練班」中，會用什麼方式來改善，依作者的經驗，在半天的密集訓練後，通常就會獲得大幅校準。

除了前面的相等賭局，還有：

重複與反饋

針對先天普遍的過度自信狀況，具體的訓練：

• 用大量題目 + 相等賭局測試
• 「先直覺做 - 公布答案 - 再做一次」

考慮兩個同意和反對意見

上述的重複與反饋，一開始執行的效果不佳，於是作者加入了班級討論：

• 在討論時，請人們對「每一項估計的有效性」提出同意和反對的看法
• 想出至少 2 個對你的評估有信心的理由，再想出可能錯誤的 2 個理由

加入討論之後，全班同學的尺度表現會大幅提高

反定錨

範圍題目表現很差的理由是，在我們的心理機制裡，人們直覺產生範圍的模式是：

• 直接定錨 (anchoring) 在某個數值上
• 增加上下的「誤差」，得到範圍

如此一來非常容易範圍太窄。

在訓練時，作者會：

• 單獨檢視上限和下限，把這個數值轉為是否題，例如「你是否 95% 確定他超過/低於這個數字」
• 用這種刻意訓練，來改善先天的「定錨」模式

或者使用荒謬測試 (absurdity test)：

• 從一個寬到荒謬的範圍開始，
• 逐漸刪除你知道極不可能的數值，有意識地慢慢縮小

一樣是在克服定錨模式，把「我認為數字是多少」轉換成「什麼數字是荒謬不可能的」

常見迷思

在書中作者記錄了一些實際的對話，這裡只快速摘要作者的心得。

最常見的心理障礙：「如果不知道一個確切的數量，我就等於不知道任何事」。

• 愈是有「專家」頭銜的人，對於給出不確定的數量有愈高的心理抗拒。
• 但專家的確會「知道一些事」，這些事能轉化成量化的不確定性

遇到這種情況，作者通常會用「荒謬測試」的手法，引導專家說出「非常不可能發生的數值」，來產生 90% CI 的範圍。

在估算時，有些人會「假設」一個範圍

• 但「假設」不適合用在這裡，因為假設不是一個你真正確定的東西
• 此時，你大可以放寬範圍，來反映出你「真正確定」的資訊

校準估算的價值

在進行尺度校準前，由於人們的數字錯誤機率太高，以至於絕大多數的認為「要進行真正的數學運算」，才能獲得估計。

然而，作者認為，在進行校準以後，你可以獲得 90% CI 的範圍，因此你可以用極低成本的方式，快速建立最初的量化分析。

今日進度：90~115 頁

btw 我在 2014 買這本書時，讀到 CH6 之後放棄了，CH6 會介紹蒙特卡羅風險分析模型，是一個數字含量較高的章節，我應該是在看完 CH6 後產生了心理上的厭惡感XD

先回顧一下上次的失敗⋯⋯幫自己做一些心理建設⋯⋯