今天我們先從馬可夫模型 (Markov Model) 開始聊聊他是如何用在音樂作曲上的。
在第十三天時我們有聊到Hiller 跟 Isaacson在1957年利用馬可夫鏈 (Markov Chain) 來產生隨機音符，之後再利用和聲與復調的規則去測試這些結果並選擇符合規則的材料，再將這些材料修改並組合成弦樂四重奏Illiac。

那麼首先我們先來介紹什麼是馬可夫模型。

馬可夫模型 (Markov Model)

由馬可夫開頭的術語很多，首先我們先來介紹幾個重點：

馬可夫性質:
馬可夫性質是機率論中的一個概念，如果一個隨機過程在給定當下的狀態以及所有過去的狀態情況下，他的未來狀態的條件機率分佈只依賴於當前的狀態;也就是說，過去的狀態 (該過程的歷史軌跡) 與當下狀態為獨立事件，這樣的隨機過程就具有馬可夫性質。
看不懂的話沒關係，後面有範例說明。

馬可夫過程:
具備有馬可夫性質的過程就稱為馬可夫過程。

馬可夫鏈:
具備離散狀態的馬可夫過程，即為一個馬可夫鏈。

馬可夫模型:
透過馬可夫過程生成序列算法模型。

至於馬可夫相關公式的部份我就不貼了，相信上面這些應該有些人已經看不太下去了，我們直接給例子來做說明。

如果今天把我每次去鹽酥雞攤點的東西的機率給設定好，種類有鹽酥雞、魷魚、豆腐這三種，每一次只能點一樣。

如果我們把機率設定為:
這次點的是鹽酥雞的話，
下次點鹽酥雞的機率為25%； 魷魚的機率為40%； 豆腐的機率為35%、
如果這次點了魷魚的話，
下次點鹽酥雞的機率為40%； 魷魚的機率為25%； 豆腐的機率為35%、
如果這次點了豆腐的話，
下次點鹽酥雞的機率為35%； 魷魚的機率為45%； 豆腐的機率為20%。
如果我每天都照三餐去光顧的話，假設我第一天的第一餐點了魷魚，請問一個月後的第一餐，我吃到以上三種食物的概率是什麼?

我們可以把我每次吃完下一次會吃的狀態畫出來如下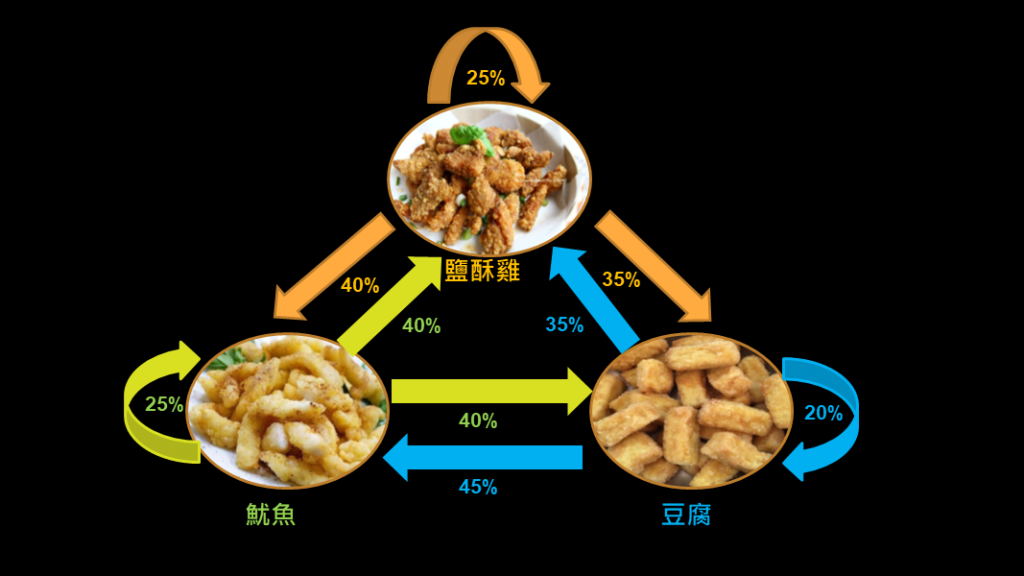

所以在我第一餐吃完魷魚後，下一餐我有40%的機率會改吃鹽酥雞，25%的機率繼續吃魷魚，35%的機率改吃豆腐。

而再根據我第二餐選到了什麼，又可以得出我第三餐吃什麼的機率，以此類推，在我吃了一個月後的第一餐，我最大的概率應該是
.
.
.
.
.
.
送醫院

那我們再回到前面說的馬可夫性質:
如果一個隨機過程在給定當下的狀態以及所有過去的狀態情況下，他的未來狀態的條件機率分佈只依賴於當前的狀態;也就是說，過去的狀態 (該過程的歷史軌跡) 與當下狀態為獨立事件。
也就是說如果我今天中餐吃了鹽酥雞了，那麼我晚餐要吃什麼，跟我今天早餐、昨天晚餐午餐早餐還有再之前的每一餐都沒有任何關係，唯一有關係的就是我現在要做決定當下(晚餐)的前一餐(午餐)吃的魷魚。

以上就是一個馬可夫鏈的簡單範例，那麼明天我們再繼續馬可夫鍊的部份來聊聊怎麼用它來實做音樂。