提醒：本篇承接第三章

讓我們說回那顆樹

既然樹是我們遊戲場景的主體之一，首先當然是要來整修一下我們的樹，此時我意外發現有個很讚的教學影片：
Fractal Tree Part1
Fractal Tree Part2

給大家參考有別於第三章實作的方式，它畫樹的方式更單純，代碼相當簡短：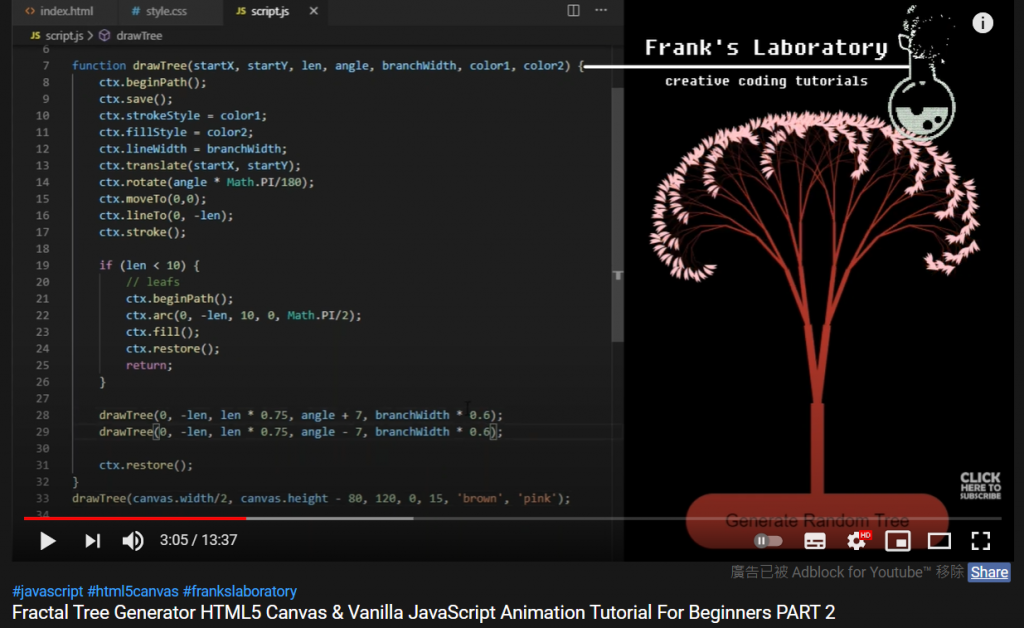

不過這是因為該影片從碎形(Fractal)開始討論，意即每個樹枝節點都是重複的形狀和角度、長度比例，因此無須用物件的形式去儲存，只要不斷遞迴畫出來即可。

如果不考慮對樹做太多隨機性的操作，這會是一個很讚的選擇。

修飾樹的形狀

剛好影片中又用到貝茲曲線，我們就來填個坑，當初第三章說要畫Y型樹枝，結果不了了之，其目的主要在於添加一些扭曲蜿蜒的效果：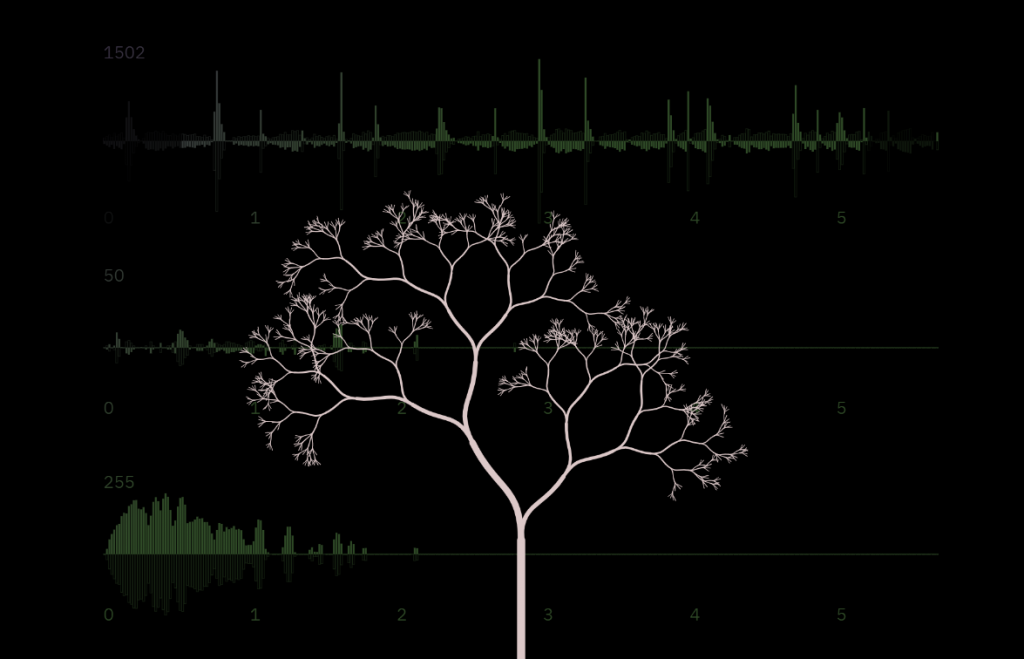

不過我覺得比較像是愛心尾端的形狀xd

在第四章的附錄我們有提到，貝茲曲線有四個點(起始點p0、控制點p1、控制點p2、終點p3)，在Canvas的繪圖中，也曾提過，每次繪製路徑都有一個起始點，可以是moveTo(x0, y0)來指定，或者lineTo(x0, y0)一邊繪製一邊移動到新的起始點，已知起始點的情況下，我們只要給足剩下的條件便能畫出貝茲曲線。

因此，貝茲曲線的函數需要另外三個參數：context.bezierCurveTo(x1, y1, x2, y2, x3, y3);

同時上次我們說到，為了讓線段能平滑的銜接，控制點會受到上一條曲線(角度)影響，也就是node.father.theta，我們希望讓樹枝能沿著上一個樹枝的方向曲折，最後才回到該樹枝的方向node.theta，

for(let N = 1; N < treeNodes.length; N++){
    let node = treeNodes[N];
    let theta1 = node.father.theta / 180 * Math.PI,
        theta2 = node.theta / 180 * Math.PI;
}

該處來自第三章的今天來學習畫一顆樹 IV

接著就能求出第一個控制點，用樹枝本身的長度一半為長度剛剛好：

x1 = x0 + 0.5 * r * Math.cos(theta1)
y1 = y0 - 0.5 * r * Math.sin(theta1)

第二個控制點同理，剛好在原本節點(x0,y0)和(x3,y3)相連的線上：

x2 = x0 + 0.5 * r * Math.cos(theta2)
y2 = y0 - 0.5 * r * Math.sin(theta2)

終點則不變，和當初設定相同：

x3 = x0 + r * Math.cos(theta2)
y3 = y0 - r * Math.sin(theta2)

完整程式碼如下：

Tree.prototype.Draw = function(){
    for(let N = 1; N < treeNodes.length; N++){
        let node = treeNodes[N];
        let x = node.father.endX,
            y = node.father.endY,
            r = node.r * Math.pow(node.grow, 1 + 3 * N/treeNodes.length),
            theta1 = node.father.theta / 180 * Math.PI,
            theta2 = node.theta / 180 * Math.PI;
        context.beginPath();
        context.moveTo(x, y);
        context.bezierCurveTo(x + 0.5 * r * Math.cos(theta1),
                              y - 0.5 * r * Math.sin(theta1),
                              x + 0.5 * r * Math.cos(theta2),
                              y - 0.5 * r * Math.sin(theta2),
                              x + r * Math.cos(theta2),
                              y - r * Math.sin(theta2));
        context.lineWidth = 0.5 + Math.pow(r, 1.1)/30;
        context.strokeStyle = 'rgba(220, 200, 200, 1)';
        context.stroke();
    }
}

r = node.r * Math.pow(node.grow, 1 + 3 * N/treeNodes.length)是讓樹枝依序(遞迴的順序)長出來的一個新寫法，還沒下定論，所以不特別討論

樹的分支

在樹枝的建構式，稍作修改，關於到底要遞迴幾次這個問題，當初我們並沒有討論，而是很懶惰的丟了一個times參數進去，就當沒事了，不過卻很值得思考，因為每多一層遞迴，樹枝的數量都會呈指數增加，太多影響效能，太少則枝葉不夠茂盛，必須找個平衡點。

首先思考點可以在於，在視覺上，遞迴到什麼程度就看不到了呢？眼睛對像素值的判斷是有限的，何況有些小細節，不見得會注意的到，那我們就從這裡下手，實測之後大約在樹枝長度為10px以下停止遞迴時，算是一個畫面表現最佳的時候，那麼就以這為最低基準去設計，不過，為了避免真的遞迴太多次，我們同樣提供一個times參數作為極限值：

let Stick = function(father, shrink_diff, angleOffset, times){
    this.father = father;
    this.r = this.father.r * (shrink_diff);
    this.theta = this.father.theta + angleOffset;
    if(this.r < 20 || times < 0){
        return this;
    }
    // 以下略
    // ......
}

當初我們有給設定一個RATIO，使畫布大小為2倍，因此20實際上表示10px
後續針對效能，估計可以給定一個範圍，比如20~40，在畫面跑不動的時候簡化它

接著，在末端的部分通常會特別茂盛，因此我們也定下一個值40（20 x 2），來作為是否進入末端的判斷基準，

let shrink = 0.65 + random(0.1);
let diff = random(0.3) - 0.15; // +-0.15
if(this.r > 40)
    this.son = [new Stick(this, (shrink - diff), 30 * (diff + 1), times - 1),
                new Stick(this, (shrink + diff), 30 * (diff - 1), times - 1)];
else
    this.son = [
        new Stick(this, (shrink - diff), 30 * (diff + 1), times - 1),
        new Stick(this, (shrink + diff), 30 * (diff - 1), times - 1),
        new Stick(this, (0.7 + random(0.1)), 30 * ( 0.5 + diff), times - 1),
        new Stick(this, (0.7 - random(0.1)), 30 * (-0.5 - diff), times - 1)];

該處新增了用diff去影響樹枝的走向，使其更富有隨機性
原版可參考第三章開篇 今天來學習畫一顆樹 I

這邊我將末梢的部分進行著色，就可以看的很清楚

每次遞迴長度的遞減比率約為0.5~0.9之間，因此進入20~40的範圍時，有些會遞迴1次，有些會遞迴2次，便可為末梢帶來更多不同變化。

後記

今天有些疲倦，不知道是否太久沒運動了(昨天跑去游泳)，結果今天躺了一整天ww，把假日都浪費掉了，本來想著可以早點完成這趴，又不可避免的要拆成兩篇了