1. 同時搞定TensorFlow、PyTorch (一)：梯度下降。
2. 同時搞定TensorFlow、PyTorch (二)：模型定義。
3. 同時搞定TensorFlow、PyTorch (三) ：資料前置處理。
4. 同時搞定TensorFlow、PyTorch (四)：模型訓練。

前言

TensorFlow、PyTorch 是目前佔有率最高的深度學習框架，初學者常會問『應該選擇PyTorch或 TensorFlow套件』，依個人看法，PyTorch、TensorFlow好比倚天劍與屠龍刀，各有擅場，兩個套件的發展重點有所不同，例如在偵錯方面，PyTorch比較容易，但TensorFlow/Keras建模、訓練、預測都只要一行程式，另外，物件偵測主流演算法YOLO，第四版以TensorFlow開發，第五版則以PyTorch開發，若我們只懂TensorFlow，那就無法使用最新版了。

其實PyTorch與TensorFlow基本設計概念是相通的，只要採用相同的approach，就可以同時學會兩個套件，在後續的介紹及範例程式我們會印證這個想法。

差異比較

PyTorch 認為兩個主要對手，『TensorFlow 1.x版把簡單的事情複雜化』，『Keras把複雜的事情太過簡化』，因而促使TensorFlow 2.x版依據Keras規格重新開發並納入TensorFlow中，現在Keras已變成TensorFlow最重要的模組。

而PyTorch特色如下：

1. Python First：PyTorch開發團隊認為Python及相關套件功能已經相當強大，不須另外發明輪子(Reinvent the wheel)，直接與Python生態環境緊密結合。
2. 除錯容易：TensorFlow/Keras 提供 fit 一行指令即可進行模型訓練，雖然簡單，但不易偵錯(Debug)，PyTorch須自行撰寫優化求解的程序，雖然繁瑣，但在過程中可插入任意的程式碼偵錯或查看預測結果、損失函數變化，不必等到模型訓練完成。
3. GPU 記憶體管理較佳，筆者使用GTX1050Ti，記憶體只有4GB 時，同時執行2個以TensorFlow 開發的Notebook 檔案時，常會發生記憶體不足的狀況，但使用PyTorch，即使3、4 個Notebook 檔案也沒有問題。
4. 程式可自行決定變數及模型要在 CPU 或 GPU 運算：雖然比較麻煩，但可優化記憶體的使用，TensorFlow則是自行偵測GPU，如果有。則預設會使用GPU運算，反之，會使用CPU。
5. C/C++整合：PyTorch 提供C/C++ extension API，有效整合，不需橋接的包裝程式(wrapper)。

另外，文件說明還是以TensorFlow/Keras較為詳盡，且較有系統性，PyTorch方面，筆者常須依靠谷大哥搜尋，這也是筆者撰寫PyTorch入門書籍的原因。

一致的學習路徑

雖然存在以上差異，PyTorch與TensorFlow基本設計概念是相通的，採用相同的approach，可以同時學會兩個套件，以下我們以一些簡單範例印證這個想法。

梯度下降法是神經網路主要求解的方法，計算過程會使用張量(Tensor)運算，另外，在反向傳導的過程中，則要進行偏微分，計算梯度，如下圖：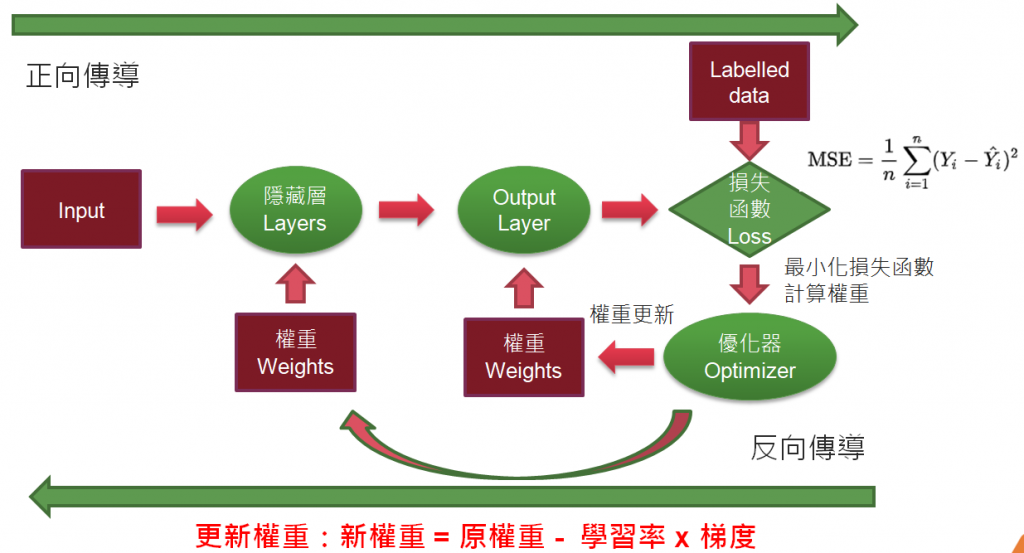

圖一. 神經網路求解過程

基於上述求解過程的需求，大多數的深度學習套件至少會具備下列功能：

1. 張量運算：包括各種向量、矩陣運算。
2. 自動微分(Auto Differentiation)：透過偏微分計算梯度。
3. 各種神經層(Layers) 及神經網路(Neural Network) 模型構建。

因此，學習的路徑可以從簡單的張量運算開始，再逐漸熟悉高階的神經層函數，以奠定扎實的基礎。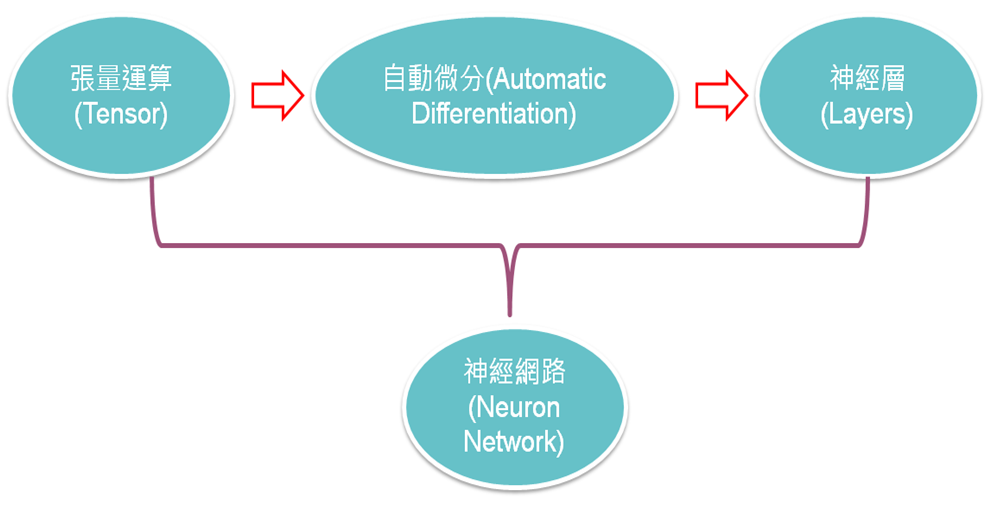

圖二. 神經網路學習路徑

優化求解

神經網路通常會有很多神經層，每一層又有很多神經元，如果加上 Activation Function，要以純數學求解相當困難，因此通常會使用梯度下降法，逐步逼近最佳解的方式，求得近似解。相關說明可詳閱『Day N+1：進一步理解『梯度下降』(Gradient Descent)』、『Day 02：梯度下降與自動微分』，這裡只說明TensorFlow/PyTorch的實作。

以 為例，求解最小值。

1. 先以手工計算梯度：的一階導數為2X，參見 dfunc 函數。

# 載入套件
import numpy as np
import matplotlib.pyplot as plt

# 損失函數
def func(x): return x ** 2

# 損失函數的一階導數:dy/dx=2*x
def dfunc(x): return 2 * x

2. 定義超參數：之後可任意改變參數值，依然可以求得最小值。

# 超參數(Hyperparameters)
x_start = 5     # 起始權重
epochs = 15     # 執行週期數 
lr = 0.3        # 學習率 

3. 求解：參照圖三，進行反向傳導，更新權重。

# 梯度下降法 
def GD(x_start, df, epochs, lr):    
    xs = np.zeros(epochs+1)    
    x = x_start    
    xs[0] = x    
    for i in range(epochs):         
        dx = df(x)        
        # 更新 x_new = x — learning_rate * gradient        
        x += - dx * lr         
        xs[i+1] = x    
    return xs

# *** Function 可以直接當參數傳遞 ***
w = GD(x_start, dfunc, epochs, lr=lr) 
print (np.around(w, 2))

4. 求解過程視覺化：由初始點5開始，逐步逼近找到最佳解。

t = np.arange(-6.0, 6.0, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(w, func(w), c='r', marker ='o', markersize=5)    

# 設定中文字型
plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei'] # 正黑體 
plt.rcParams['axes.unicode_minus'] = False # 矯正負號

plt.title('梯度下降法', fontsize=20)
plt.xlabel('X', fontsize=20)
plt.ylabel('損失函數', fontsize=20)
plt.show()

執行結果如下：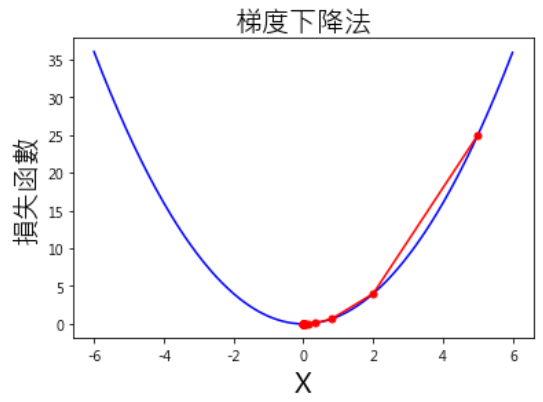

圖四. 求解過程視覺化

TensorFlow的作法

修改 dfunc 函數，改用 TensorFlow/PyTorch 提供的自動微分及梯度計算功能，取代 dfunc 函數的程式碼如下：

def dfunc(x_value): 
    x = tf.Variable(x_value, dtype=tf.float32) # 宣告 TensorFlow 變數(Variable)
    with tf.GradientTape() as g: # 自動微分
        y = x ** 2                # y = x^2
    dy_dx = g.gradient(y, x)     # 取得梯度
    return dy_dx.numpy()         # 轉成 NumPy array

PyTorch的作法

def dfunc(x): 
    x = torch.tensor(float(x), requires_grad=True)
    y = x ** 2 # 目標函數(損失函數)
    y.backward()
    return x.grad

完整程式請自『這裡』下載，程式名稱為 src/03_02_自動微分.ipynb。

結論

TensorFlow/PyTorch 基本設計概念是一致的：

1. 張量(Tensor)均與NumPy陣列相容，不論是資料結構或是運算，包括 Broadcasting 機制。
2. 自動微分、梯度下降也是如此，只是語法不同而已。

下一篇我們繼續比較神經網路及神經層的差異。

以下為工商廣告:)。
PyTorch：
開發者傳授 PyTorch 秘笈

TensorFlow：
深度學習 -- 最佳入門邁向 AI 專題實戰。