Assumptions of a Linear Regression

使用線性回歸之前, 需要評估資料的特性有沒有滿足以下五點
若有滿足才可以使用線性回歸
不過課程沒有針對這些特性做過多講解, 之後再找時間研究...

1. Linearity 數據是線性

2. Homoscedasticity 數據要有同樣方差

3. Multivariate normality 多元正態分佈

4. Independence of errors 誤差獨立

5. Lack of multicollinearity無多重共線性

Multiple Linear Regression

我們先來看一個例子

此例中的變數變多了, 因此我們可以用多元線性回歸來當作模型
不過我們也發現只有state 不是數字, 很明顯state是分類數據
分類數據是沒有辦法排序的, 表示的是一種類別
所以要將state改成dummy variable才可當當作變數套入模型
所以我們新增加兩行資料分別是NewYork 和 California

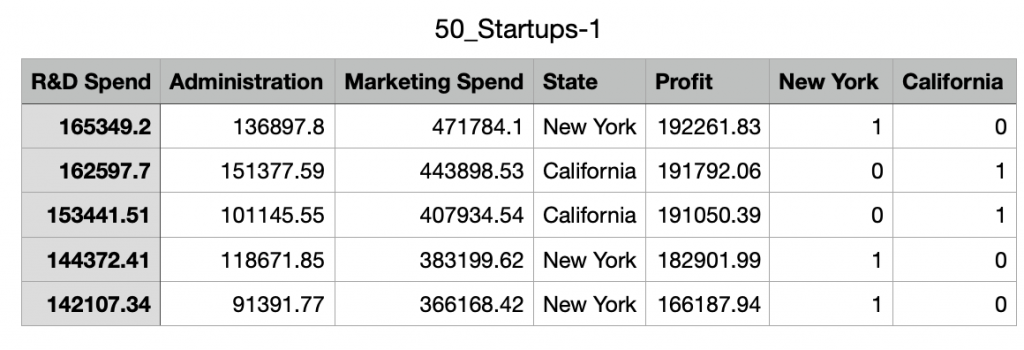
不過其實California 欄位可以忽略

因為當NewYork 欄位等於0 就代表是California 了
所以我們的公式可以變成 y = a0 + b1X1 + b2X2 + b3X3+ b4X4
X1~X4 代表所有的column 欄位
y 代表profit

老師提到一個有趣的問題是：
Q: state一定要用1,0 嗎？可以用100, 0 嗎？ 可以用1, -1 嗎
A: 可以, 但雖然表面上我們對NewYork 的值進行縮放, 但其實是沒有影響的
因為縮放的影響其實被包含在b4
Ex: 假設我們的模型已經擬合好了, 但我們將NewYork 由1 放大100倍(California 不變)
相當於b4 會被縮小100倍, 因此b4*D1 = 1/100 * 100 -> 達到的效果一樣
同理, 1, -1 是由b0 和b4 控制的
因此無論我們選擇什麼數字都是一樣的, 不過通常我們還是會用1,0 來表示

虛擬變量的陷阱

假設我們把california 的變數也加進公式可以嗎？
其實California=1-NewYork, 代表他們兩個之間存在著明顯的線性關係
=> 這就不滿足非多重共線性的條件了
因此假設今天有三個州, 就要保留兩個州當作虛擬變量(Always omit one dummy variable)
最後一個必須移除