今天來講的分類方法是 LDA 線性區別分析。
在分類的區隔明顯、資料量較小時,它的分類表現可能比羅吉斯回歸還要好,除此之外,它可以分類多個種類,不只有二元。
線性區別分析(Linear Discriminant Analysis,LDA)是一種監督式學習的分類方法,它是Bayes’ Theorem 在分類上的應用。
Bayes’ Theorem: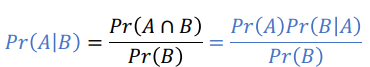
(where A and B are two events and Pr(B) not 0.)
應用在分類上: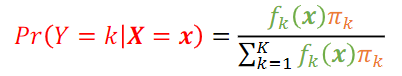
Linear discriminant function: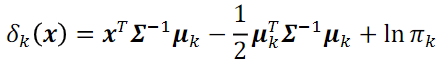
決策邊界(Decision boundary):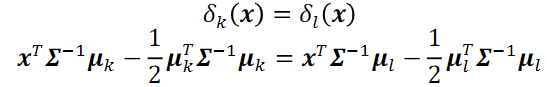
LDA就是想找到不同類別、事件的特徵做一個線性組合,以能夠特徵化或區分它們(不同類)。
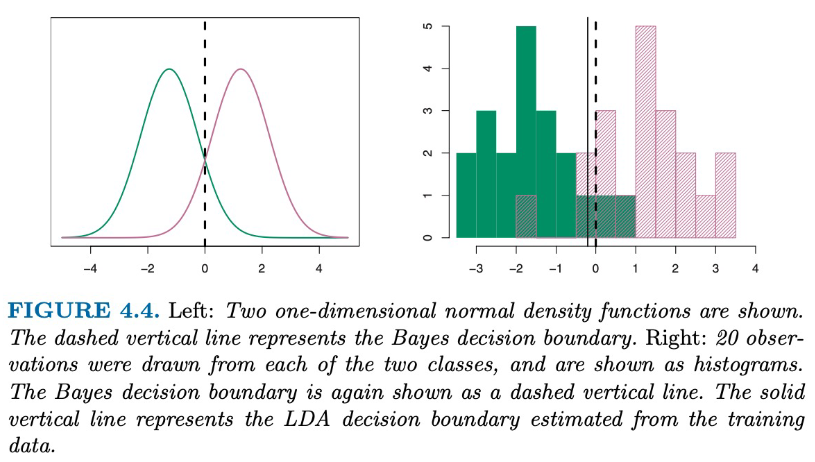
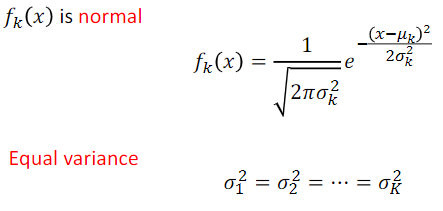
[注意]
⇒ 各 Class density ( = Pr(X=x|Y=k) ) 要服從多元常態 (多元高斯 Multivariate Gaussian Distribution) 分布,且相同變異( common covariance matrix)。
= Pr(X=x|Y=k) ) 要服從多元常態 (多元高斯 Multivariate Gaussian Distribution) 分布,且相同變異( common covariance matrix)。
⇒ 資料處理:
為了將資料處裡成適合使用 LDA 模型的形式,可以先將資料標準化後,確保資料服從常態N(0,1)的分布。
LDA算是PCA(Principal Component Analysis, 主成分分析)的一種延伸。
他們兩者都希望找到投影軸讓資料投影下去後分散量最大化,但 LDA 是Supervised Learning目標是要分類,所以找的投影軸會希望能夠將不同類組的資料分越開越好(組間變異大、組內變異小)。
除此之外,LDA 又常被稱為 Fisher’s Discriminant Analysis ,因為能夠使用費雪準則 (Fisher criterion)最佳化「組間/組內的分散量」找出投影矩陣。
要進行 LDA 線性區別分析時會使用到MASS套件中的lda( )函式。
## LDA model
lda.model <- lda(groups ~ X, data= data, prior= proportions)
## predict ()
predict(lda.model, data = testing_data) $class
## confusion table
table( predict= predict(lda.model, data = testing_data)$class,
actual = testing$groups )
# Model accuracy
mean(predict(lda.model,data =testing_data)$class == test.transformed$Species)
prior: 用來指定總體上每組出現的機率,即先驗機率 。
caret, tidyverse套件用來標準化變數。# 觀察資料
data("iris") #以R內建資料iris示範
names (iris) #資料裡,各變數名稱
dim (iris) #資料筆數, 變數數量
str(iris) #列出資料內每個欄位的狀態
summary(iris) #連續型資料:會看到 Qu. #類別型資料:會看到不同數值的資料個數
head(iris) #呈現前6筆資料
# 將資料分為60%訓練和40%測試集
set.seed(123)
train.index = sample(x=1:nrow(iris), size=ceiling(0.6*nrow(iris) ))
training = iris[train.index, ]
testing = iris[-train.index, ]
## 標準化資料
install.packages("tidyverse")
install.packages("caret")
library(tidyverse)
library(caret)
theme_set(theme_classic())
preproc.param <- training %>% preProcess(method = c("center", "scale"))
# 使用preproc.param參數 轉換(標準化)資料
training_transformed <- preproc.param %>% predict(training)
testing_transformed <- preproc.param %>% predict(testing)
建立 LDA 模型:
install.packages("MASS")
library(MASS)
## 建立 LDA 模型
# Iris Data 的實際 prior先驗機率為1:1:1
lda.fit <- lda(Species~.,prior=c(1,1,1)/3, training_transformed)
lda.fit
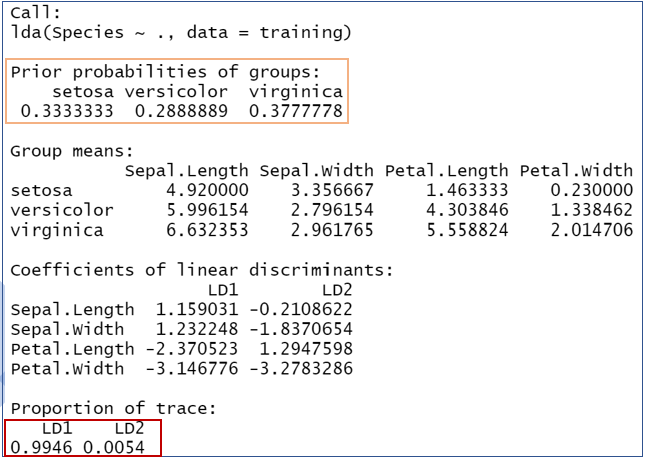
LD1 與 LD2 表示為判別係數。
代表判別函式能夠解釋原來特徵之中變異資料所佔的比例。而 LD1 達 99.46% 表示已足夠用來判斷資料。
## 預測
# output: predicted class(groups)
predict(lda.fit, testing_transformed)$class
# true class(groups)
testing_transformed$Species
## Confusion matrix and accuracy
lda.class<-predict(lda.fit, testing_transformed)$class
table(predicted = lda.class, actual = testing_transformed$Species) # Confusion matrix
mean (lda.class == testing_transformed$Species) # accuracy
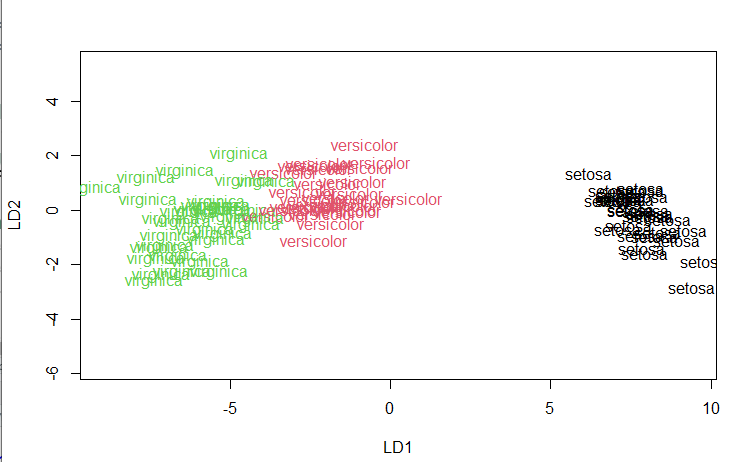
分類結果:
plot(lda.fit, #lda
col = as.integer(training_transformed$Species), #color
cex=1) #text size
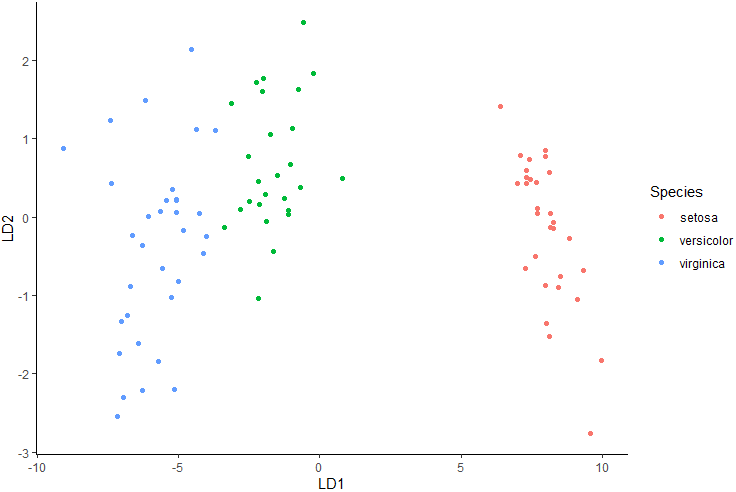
install.packages("ggplot2")
library(ggplot2)
lda.data <- cbind(training_transformed, predict(lda.fit)$x)
ggplot(lda.data, aes(LD1, LD2)) +
geom_point(aes(color = Species))
觀察 LD1、LD2 分別貢獻的區分:
## Stacked histogram for discriminant function values
lda.pred <- predict(lda.fit, training_transformed)
ldahist(data = lda.pred$x[,1], g = training_transformed$Species)# based on ld1 # g: groups
ldahist(data = lda.pred$x[,2], g = training_transformed$Species)# based on ld2
LD1:
可以看出 LD1 已經有99.46%判斷力,其實足夠用來判斷資料。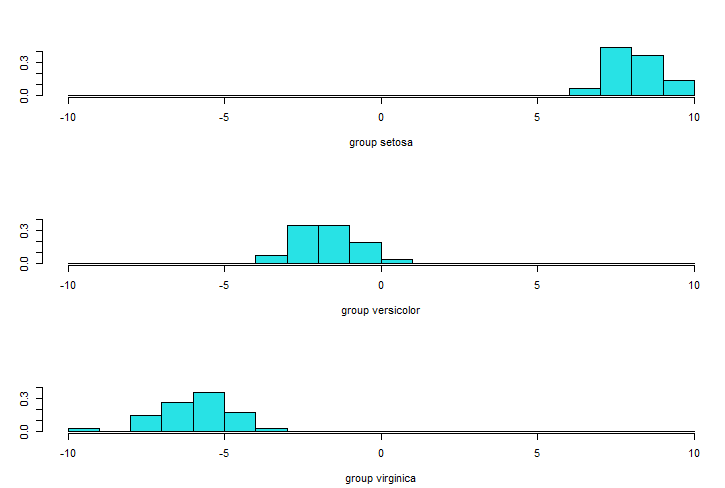
LD2: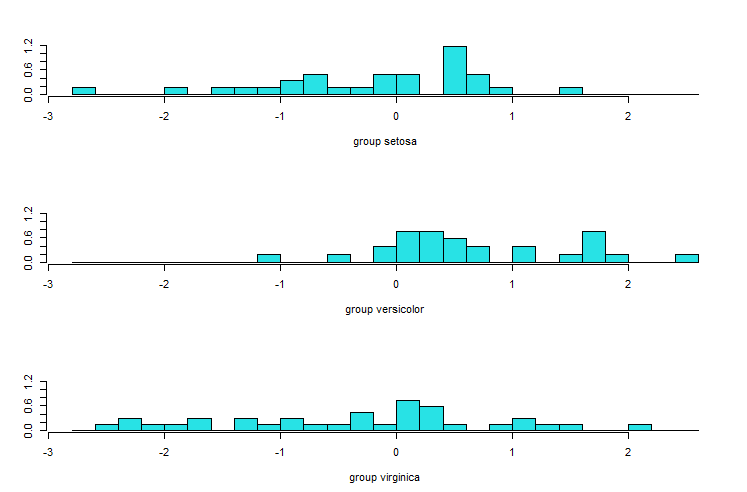
將LDA計算時的共變異數矩陣做變化時,可以延伸進行其他的區別分析:
統計與機器學習 Statistical and Machine Learning, 台大課程. 王彥雯 老師.
Linear Discriminant Analysis in R Programming
https://www.geeksforgeeks.org/linear-discriminant-analysis-in-r-programming/
Linear Discriminant Analysis in R (Step-by-Step)
https://www.statology.org/linear-discriminant-analysis-in-r/
Articles - Classification Methods Essentials
Discriminant Analysis Essentials in R
http://www.sthda.com/english/articles/36-classification-methods-essentials/146-discriminant-analysis-essentials-in-r/
機器學習: 降維(Dimension Reduction)- 線性區別分析( Linear Discriminant Analysis)(@Tommy Huang)
https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92-%E9%99%8D%E7%B6%AD-dimension-reduction-%E7%B7%9A%E6%80%A7%E5%8D%80%E5%88%A5%E5%88%86%E6%9E%90-linear-discriminant-analysis-d4c40c4cf937
