模型學習完成之後，怎麼驗證模型學習的效果好不好，預測準不準確，就是今天要講的模型的評價方法。

交叉驗證（Cross validation）

監督式學習需要有資料和答案的樣本來讓機器學習，最終要看的是對未知的資料能否做出準確的預測。所以要先準備好對機器來說未知的資料，將手頭的資料分為學習用的訓練集（已知資料）和確認用的測試集（未知資料），這種方法稱為交叉驗證。

資料的集合我們稱為資料集（dataset）

• 訓練集（Training set）
  用來訓練的已知資料，用來訓練機器學習，主要是靠答案的回饋來調整函數的參數來矯正誤差。
• 測試集（Test set）
  用來測試的未知資料，讓完成學習的機器使用函數做預測，測試其準確性。

訓練集有可能再細分出驗證集（Validation set），如果沒有要調整 Hyperparameter（由人自由決定的參數）的話可以不用驗證集。

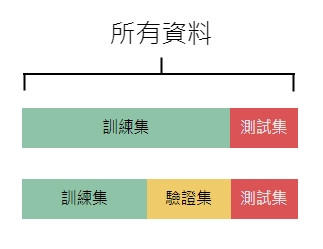
簡單來說，訓練集就是上課學習掌握知識，驗證集是作業或模擬考用來確認學習狀況調整學習方向和進度快慢，測試集就是學測做學習驗收。訓練集和測試集的資料不能重疊，否則就像學測的題目是用考古題直接出題一樣，測不出學習的成果。

那怎麼把資料分成訓練集和驗證集呢？方法有下列3種：

• Holdout 驗證
  直接用比例分成訓練集和測試集，通常測試集會取比較小的部分，像是30%或20%。
• K 折交叉驗證 （K-Fold Cross Validation）
  將資料分成 K 等分，一次取一份測試，剩下做訓練，最後取 K 次的驗證誤差（Validation Error）的平均。
• Leave one out
  其實就是 K 折交叉驗證，只是 K = 所有資料數，一次取一筆資料當測試，剩下做訓練。

比如說100筆資料取4等分做4折交叉驗證：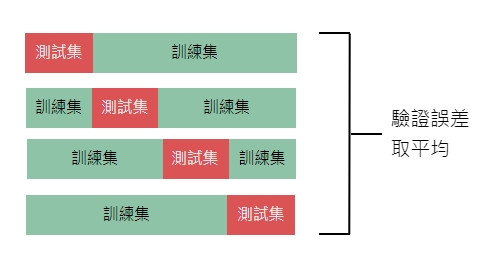

100筆資料做100折交叉驗證就是 Leave one out

混淆矩陣（Confusion matrix）

預測的準確率很重要，可以透過混淆矩陣這個工具用圖形直接看出是否把類別搞錯了，並藉此算出準確率。比方說我們目標是分類貓，將預測的結果做成一個矩陣。

用程式顯示的1000筆資料的混淆矩陣：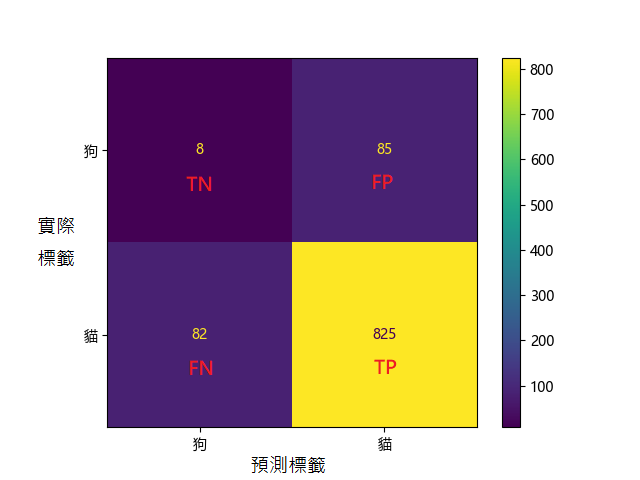

• 真陽性（TP，True Positive）
  目標的圖片分類正確（貓標示成貓）。

• 真陰性（TN，True Negative）
  不是目標的圖片分類正確（狗標示成狗）。

• 偽陽性（FP，False Positive）
  不是目標的圖片分類錯誤（狗標示成貓）。
  統計學上又稱第一型錯誤（Type 1 Error），誤報。

• 偽陰性（FN，False Negative）
  目標的圖片分類錯誤（貓標示成狗）。
  統計學上又稱第二型錯誤（Type 2 Error），漏報。

評價指標

藉由混淆矩陣，我們可以算出以下的模型的評價指標。每個指標都有合適的使用狀況。選擇最適合的評價指標來作為模型評價的依據。

接下來以剛剛的混淆矩陣來試算：

• 準確率（Accuracy）
  所有資料都預測成功的比例。
  最基本的評價指標，但缺點是非目標的資料過少會造成準確率雖然高但非目標都判斷錯誤的可能性。
  
  準確率 = (825+8)/1000 = 0.833

• 精準率（Precision）
  預測目標被成功預測的比例。
  適合狀況：想要預測出是否符合客戶的喜好。預測是客戶的喜好商品，實際上真的是喜好商品的比例。
  
  精準率 = 825/(825+85) = 0.906

• 召回率（Recall）
  實際目標被成功預測的比例。和精準率成反比。
  適合狀況：醫療診斷這種不允許錯誤的情況。真正有生病的人中，被判斷出生病的比例。
  
  召回率 = 825/(825+82) = 0.909

• F値（F-measure）
  精準率和召回率的調和平均值。
  能夠均衡的作為綜合性指標。
  
  F值 = (2×0.906×0.909)/(0.906+0.909) = 0.907

ROC曲線（Receiver operating characteristic curve）

除了用混淆矩陣，我們也能用圖形化直觀的看出學習效果如何，也就是 ROC 曲線，用來表示真陽性率和偽陽性率關係的曲線，

• 真陽性率（TPR，True Positive Rate）
  其實就是 Recall 率。陽性正確預測成功的比例。
  
• 偽陽性率（FPR，False Positive Rate）
  誤報率，陰性被誤報成陽性。
  

我們以 Day7 邏輯回歸的乳癌腫瘤範例，加上交叉驗證後確認測試集的學習效果如何。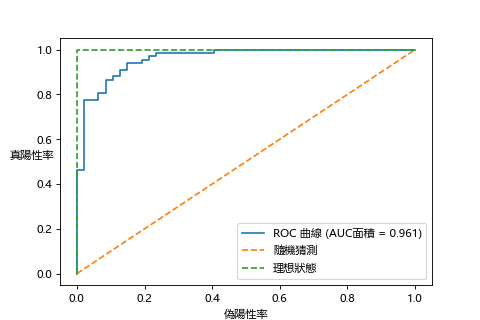

越靠近左上角，真陽性率越接近 1 （100%），偽陽性率越接近 0 （0%）是最好的狀態。

而 AUC（Area Under the Curve）則是曲線下面的面積，面積越大，表示模型性能越好。因此也可以用數字表示學習的效果。

• AUC = 1（1×1 的正方形面積）
  完美情形，理想狀況。
• AUC > 0.5（對角線面積）
  優於隨機猜測，有預測價值。
• AUC <= 0.5
  等於或差於隨機猜測，無預測價值。

乳癌的話還是要確認一下 Recall 率比較保險，用程式算出 Recall 率約有 92.5%。

模型的可解釋性

越來越多國家的貸款，特別是歐洲國家，是由電腦來決定是否借錢給你。如果我們拿不到貸款，是不是會很想知道為什麼電腦說不，這就需要電腦可以給個理由說出為什麼做這樣的決定。

也因此可解釋的 AI （XAI，Explainable AI）已經變得越來越重要。尤其是攸關人命的醫療單位，如果 AI 說你這個病沒什麼大礙，或是說你得了很嚴重的病，那根據在哪裡，萬一因此醫死人是誰要負責？

因為機器學習是透過數學函數去逼近一個最佳解，很難去解釋這個函數和裡面的參數到底代表什麼意義，更別說深度學習一層一層自動去交叉運算出來的結果，這種不知道內部運作的原理，我們稱為 AI 的黑盒子（Black Box）。目前能透過將演算的過程可視化來幫助我們作出解釋，像是一些工具 LIME 和 SHAP。

• LIME（Local Surrogate Interpretable Machine Learning）
  將複雜的模型用近似線性模型的方法來解釋。Github 上也有公開的 library 可以用。
  例如：藉由標記貓和非貓的特徵來解釋如何判斷出貓。
  
  —— 圖片出處：Github - Lime

• SHAP
  主要是解釋每個特徵對結果的影響（貢獻度），是一個 Open source library。
  例如：透過波士頓房價資料集解釋 LSTAT（從事低收入職業的人口百分比）和 RM（住宅中的平均房間數）對房價的影響很大。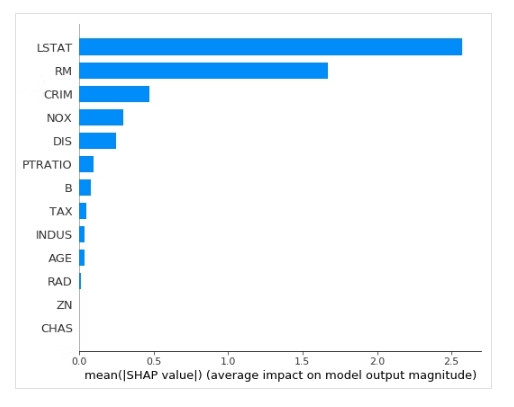
  
  —— 圖片出處：SHAP

模型選擇

學習模型太過複雜的話，容易出現過度學習，學習的計算成本（花費的時間）也會變多。根據奥卡姆剃刀定律（Occam's Razor），如果精度相同，就應該盡可能選擇單純的模型。Simple is the best 的方針。

而這個方針可以用赤池訊息量準則（Akaike information criterion）這個公式來評估，精度越高參數越少則 AIC 越小。

L=概似函數（Likelihood），k 是參數個數

補充資料

• 範例程式 - 混淆矩陣和評估指標
• 範例程式 - 交叉驗證，ROC 曲線和 AUC
• XAI 的文章大幅增加，以及在各領域的占比

立即複習

1. 資料集通常會分為已知資料和未知資料來對模型做驗證，這兩種資料集分別叫做？
2. 交叉驗證的 K fold驗證是指 K=5 時，將 100筆資料分成幾等分？
3. 混淆矩陣的偽陽性是指什麼？算是誤報還是漏報？
4. 評價指標用在醫療診斷時最重要的指標是？
5. ROC曲線用視覺判斷，曲線越靠近左上還是右下比較好？
6. ROC曲線用數字判斷，AUC面積至少要大於多少才有預測價值？
7. 精度相同時應該選擇複雜的模型還是簡單的模型？

參考資料

• 深層学習教科書 ディープラーニング G検定（ジェネラリスト）公式テキスト
• Wikipedia - 交叉驗證
• Wikipedia - 混淆矩陣
• 科技報橘 - 全球 80% 貸款由電腦決定是否核發
• Github - Lime
• SHAP