機器學習的模型是不是還有一個沒有講？沒錯，就是神經網路！Day5 的時候我們有簡單介紹感知器和神經網路，這邊就來實際說明感知器和神經網路的基本構成，雖然神經網路最早是監督式學習，但後來由深度學習衍伸的各種模型已經橫跨了各個學習，後面應用篇再一起介紹，我們先介紹基礎篇。

感知器的構造

前面說過感知器是人工仿造的神經元，裡面的構造是設計成接受一或多個輸入，然後產生一個輸出。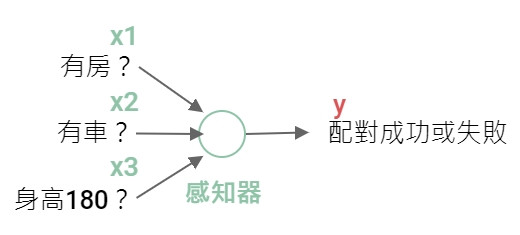

感知器的內部：

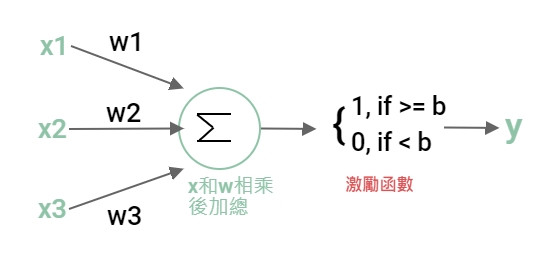
這個內部是仿造人類的神經元。接受其他神經元的刺激訊號，當刺激累積超過閥值達到動作電位會傳遞訊息給下一個神經元。

以 Day5 虛構的交友軟體為例，假設有3個因素影響你是否按下喜歡的按鈕，每個因素對你的重要性如下：

那麼感知器決定步驟如下，

1. 設定你能接受的門檻（或叫閥值，Threshold） b，假設為0.9
2. 把每個輸入乘上權重
   當你看到某位對象除了身高以外都符合：

• x1 * w1 = 0.7
• x2 * w2 = 0.4
• x3 * w3 = 0

3. 加總結果
   0.7 + 0.4 + 0 = 1.1
4. 透過激勵函數（Activation function）決定輸出
   加總結果大於門檻則輸出 1（喜歡），否則為 0（不喜歡）。
   1.1 > 0.9， 輸出為1（你默默地按下喜歡按鈕）

重要性是依人而定，權重越高代表這個因素對你越重要，而門檻越高代表你眼光高。

為了讓數學式看起來漂亮，把門檻 b 改到等式的左邊當作偏差，等式變成這樣。

這個就是感知器內部的數學計算。w（weight，權重） 和 b（bias，偏差） 都是參數（Parameter），也就是我們機器學習最終的目標，藉由調整參數來讓誤差（Error）變小，找到一個預測最準確的函數。訓練時如果數值調大誤差會變小的話就往大的方向調整，反之亦然。

感知器的問題

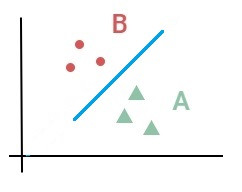
從激勵函數來看，我們最終只能輸出 0 和 1 分類。這個激勵函數我們稱為 Step 函數。只能用一條直線去做線性分類。無法做非線性分類。

線性分類	非線性分類

多層感知器（Multilayer Perceptron）

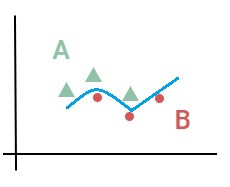一個感知器只能畫一條直線做線性分類，那非線性的分類怎麼辦呢？那就用彎的線，也就是把激勵函數的 Step 函數換成非線性的函數做分類。那多個分類怎麼辦呢？那就用多個感知器畫更多的線。這就是多層感知器，也叫神經網路（Neural Network）。

神經網路的輸入叫輸入層，輸出叫輸出層，中間各層叫隱藏層。你問隱藏層是什麼？其實就是感知器，主要是從這邊開始學習。

神經網路的問題

• 問題 1：貢獻分配問題（Credit assignment problem）
  那麼多層，到底那個參數比較重要（貢獻高），要調整誰才好不知道，這個叫貢獻分配問題。
  這個問題後來用反向傳播（Backpropagation）解決，也就是反向對多層感知器做梯度下降經由最佳化做參數調整。就是下圖反方向的數學計算。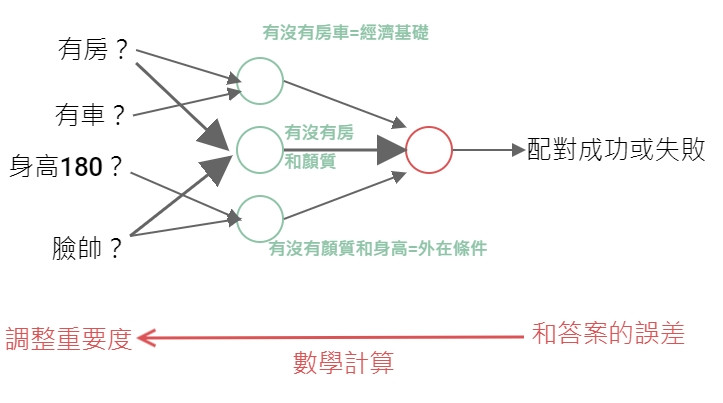
  
  由於 step 函數無法微分也就沒法透過梯度下降做學習，所以神經網路的神經元會改用 sigmoid 函數作為激勵函數來學習。

  梯度下降在 Day8 有提到，可以回顧一下喚醒記憶。
  sigmoid 函數在 Day7 有需要的話也請穿越過去。

• 問題2：梯度消失問題（Vanishing Gradient Problem）
  由於梯度下降是用微分，反向傳播時層數越多越往前面接近輸入層的梯度會有越來越小的問題，導致沒法正確地反映誤差作修正。也就是梯度消失問題。
  神經網路到這邊卡住了，既然層數加多誤差也無法變小，所以那時候 SVM 等演算法比神經網路流行。

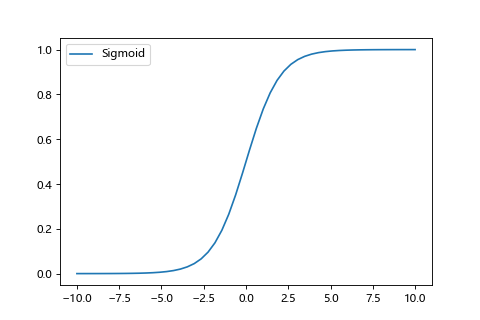
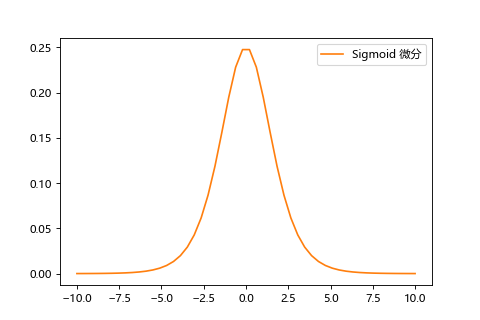
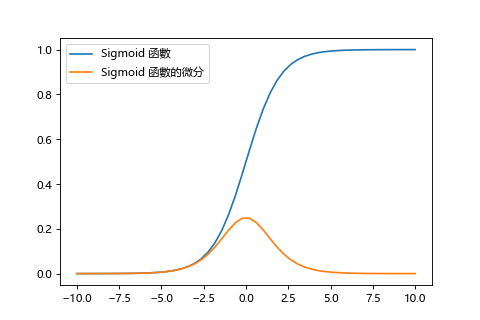
而梯度消失的原因在於，在反向傳播方法中，傳遞誤差時每層激勵函數的梯度是相乘的，但是 sigmoid 函數的微分最大值只有 0.25，使得傳播值越來越小。（0.25 * 0.25 * 0.25 ...）

sigmoid	sigmoid微分

深度學習的實現

到了2006年，多倫多大學的 Geoffrey Hinton 教授提出的自動編碼器看到了解決梯度消失問題的曙光。

雖然現在不常用這個手法，但卻是當時邁向深度學習的一大步。

自動編碼器（Autoencoder）

簡單來說就是把輸入當成輸出。透過編碼器（Encoder）壓縮輸入資料，再透過解碼器（Decoder）重建成輸出，重建過的輸出要盡可能地和原本的輸入一樣，也就是找到彼此間的最小誤差。透過這樣的手法找到最能代表這個資料的特徵。因為實際上沒有給答案，屬於無監督式學習，而編碼器做的資料壓縮，其實也就是降維。

因為輸出是被重建過的輸入，所以輸入層和輸出層的感知器個數會一樣。

以手寫數字辨識為例：

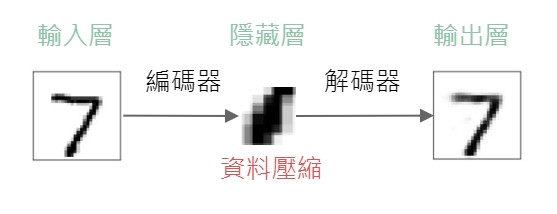
像是7的白色區域，如果壓縮這些部分而又不會造成結果失真，那就是不重要的特徵，白色區域就可以壓縮成一類資料，而數字的辨識在於黑色的特徵（橫線，斜線），壓縮到什麼程度才不會影響結果來找出最重要的特徵。

可以看到輸出層的7和原本的7稍微不同，就是因為經過資料壓縮後重建的結果。因為隱藏層是被壓縮過後的資料，所以自動編碼器的隱藏層感知器數量會比輸入／輸出層的少。

堆疊自編碼器（SAE，Stacked autoencoder）

有了自動編碼器，就可以把自動編碼器堆疊起來，做有深度的學習，構成有兩個：

• 預訓練（Pre-Training）
  以自編碼器來說就是做逐層訓練。第一個自編碼器的隱藏層當成第二個自編碼器的輸入層。也就是拿壓縮過後的資料給下一層去學習。

  舉例來說，第一層訓練 i→m→i，第二層訓練 m→n→m，由此得到 i→m→n 的結果。

• 微調（Fine tuning）
  一直做自編碼的最後還是要輸出成標籤做分類或回歸，如果是分類就是要加上激勵函數 sigmoid 函數 做二元分類或是後面介紹的 softmax 函數做多元分類。再做最後的整體學習，所以叫微調。

由於透過預訓練已經事先調整每層的權重，所以可以避免掉梯度消失。

可惜的是2006年提出的當下，GPU 的計算能力還沒有跟上，所以深層計算的速度不夠快，一般大眾的想法是神經網路也不是完全沒有用嘛（但我們還是繼續用 SVM ），直到2012年一鳴驚人後改名叫深度學習，也因此深度學習泛指 4層及以上的神經網路，也就是輸入層和輸出層，加上兩層或以上的隱藏層。

激勵函數（Activation function）

既然梯度消失問題是隱藏層的 sigmoid 函數作微分的最大值太小所導致，那麼就有人說，要不我們換其他的函數當激勵函數如何？

Tanh 函數（Hyperbolic tangent）

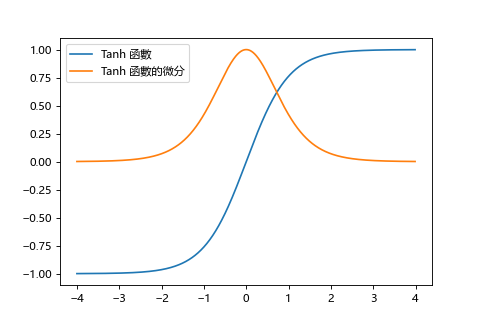
最早有想到和 sigmoid 長得很像的 tanh 函數。
不同之處在於 tanh 函數的範圍是 -1～1 而不是 0～1。
而微分的最大值為1，可以期待抑制梯度消失的效果。但只要有比 1 小的時候，還是會發生。

sigmoid	tanh

ReLU 関数（Rectified Linear Unit）

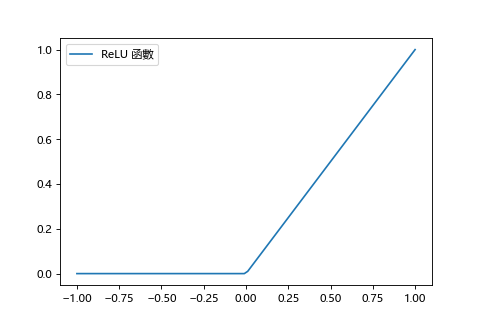
一個函數，當 x 小於0 時變為 0，當 x 大於 0 時變為線性。
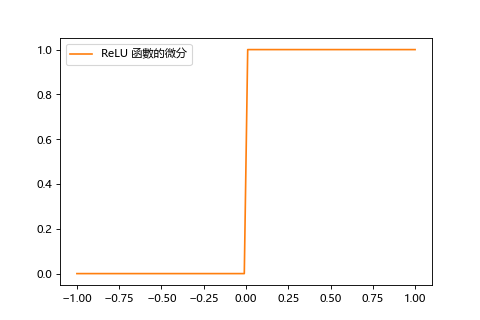
其微分在 x 小於 0 時為 0，在 x 大於0 時為 1。

ReLU	ReLU的微分

ReLU 很符合動作電位的特性，沒達到就為 0，達到就動作，目前使用ReLU當激勵函數已經是主流。
不過雖然 x 大於0時學習效率高，但小於0時梯度容易消失。作為對此的改進，還有一個即使在 x 小於0時也具有平緩斜率的激勵函數，例如 LeakyReLU。

逐層做預訓練的話速度上會慢上很多，後來演變成激勵函數替換成 ReLU 加上之後會介紹的 Skip Connection 手法可以解決梯度消失問題，不用再逐層訓練可以直接一口氣學習。

Softmax 函數

當作輸出層的激勵函數用來做多元分類。可以把各個類別的值固定在0～1，加總起來為1。用比例當成機率。例如三個分類：柴犬的機率為60%，博美犬的機率30%，雪橇犬10%，總合為100%。輸出層的感知器個數即為想要分類的種類個數。而做二元分類（0或1）通常輸出層會用 sigmoid 函數。

激勵函數列表

名稱 | 輸出 | 常用用途 |
------------- | -------------
Step | 0或1 | 早期感知器使用
Sigmoid | 0～1 | 輸出層做二元分類
Tanh | -1～1 | 隱藏層做學習（部分模型）
ReLU | 0或線性 | 隱藏層做學習（主流）
Softmax | 總和為1 |輸出層做多元分類

補充資料

範例程式 - 手寫數字辨識的 AutoEncoder
範例程式 - 各個激勵函數的微分

立即複習

1. 感知器最早只能做什麼分類？
2. 神經網路透過替換什麼可以做非線性分類？
3. 貢獻分配問題可以用什麼方法解決？
4. 梯度消失問題是因為哪個函數的微分太小所導致？
5. 自動編碼器，隱藏層的感知器個數應該比輸出的感知器多還是少？
6. 深度學習早期是使用什麼手法做深層的學習？
7. 深度學習一般是指幾層以上的神經網路？
8. 用 ReLU 函數 替換掉 sigmoid 函數可以讓梯度消失較難發生，那是要換掉哪一層的激勵函數？
9. 如果最後想要分類出4個分類，應該在輸出層的激勵函數使用什麼函數？輸出層感知器的個數幾個？

參考資料

• W3C School - Perceptrons
• Wikipedia - Autoencoder