接續上一篇的範例, 接下來學習評估結果

如何看分類器預測出的結果如何

首先用混淆矩陣來看有多少組是正確預測, 有多少組是錯誤預測
關於 Confusion matrix 這課程中沒有太多著墨, 應該是之後會補充

# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

confusion_matrix(y_test, y_pred)：

• y_true: Ground truth target values 代表真實的結果
• y_pred: Esitmated targets 預測出的結果

Run 完後在Console欄位輸入 cm 並按下enter可以看cm 的值為：
[65,3]
[8,24]

代表正確分類出的有65+24 筆, 錯誤分類的有3+8筆

畫圖

圖裡面我們需要顯示機器預測結果與實際結果
機器預測結果我們用背景顏色來顯示
實際結果我們用散點圖來顯示
背景圖怎麼畫：把每一個像素點當作一個測試資料
若一個點被歸類在結果為0 則畫成紅色
若一個點被歸類在結果為1 則畫成藍色

from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))

x_set[:, 0].min()-1 → 取age 的最小值再-1
x_set[:, 0].max()+1 → 取age 的最小值再+1
要加減1是為了讓圖的邊緣留白
x1, x2 就是一個個的小點, 用來組成背景顏色的

plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green')))

用擬合好的分類器來預測x1,x2每一個點所屬的分類, 並根據分類結果圖上顏色
紅色代表預測結果為0
藍色代表預測結果為1

plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('orange', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

接著標注x,y軸最大最小值
然後畫散點圖, 把實際結果標出來
最後加上標題, legend() 顯示點代表的意義

畫出來的圖

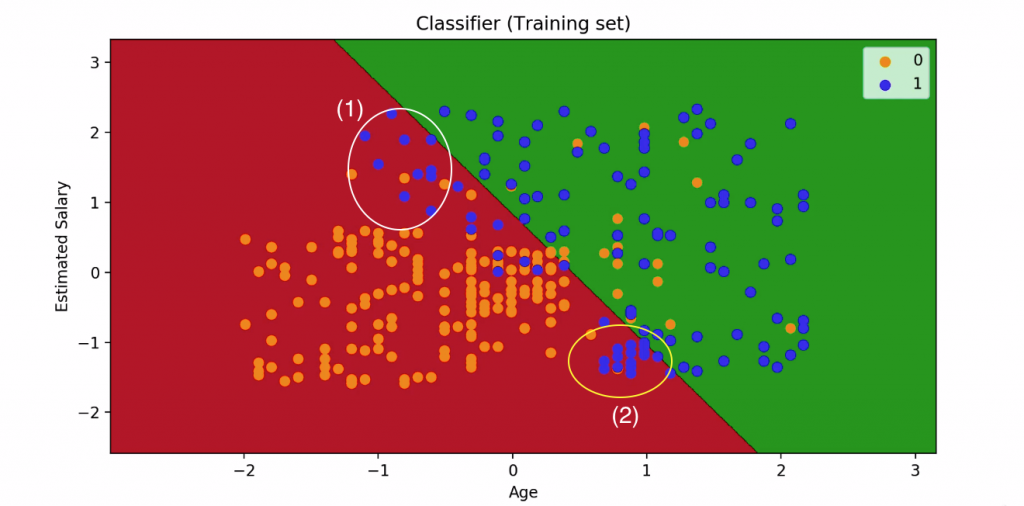
畫出來的圖可以讓我們看出分類器的分類結果
圖型中：
x軸＝age
y軸=Salary
橘點跟藍點代表訓練集裡的每一個user
藍色＝1 代表這些客戶看了廣告後有買這些車(年齡大且收入高)
橘色＝0 代表這些客戶看了廣告後沒有買這些車(年齡小且收入低)

分類器目的是要家人們做分別, 把感興趣的人和不感興趣的人分類出來
並且決定將SUV廣告投放給可能感興趣的人

中間的直線叫做“預測邊界”
是利用橘色與藍色訓練集資料所得到的邊界
再用紅色與藍色兩塊區分出0,1 兩種結果

注意圈起來的兩部分
1.左上在紅底區域的藍色點點們: 年齡比平均低, ,但收入較高, 有買車
2.右下在紅底區域的藍色點點們: 年齡比平均高, ,但收入較低, 但仍有買車
這兩塊的結果與預測值顯然不同
這是因為邏輯回歸分類器是一個廣義的線性回歸分類器, 因此預測邊界都是線性的
(二維→直線/三維→平面)
不過因為因為樣品並不是線性的, 因此要用非線性分類器才夠準確

現在我們用 test set 在畫一次
看看預測結果跟實際結果是否相同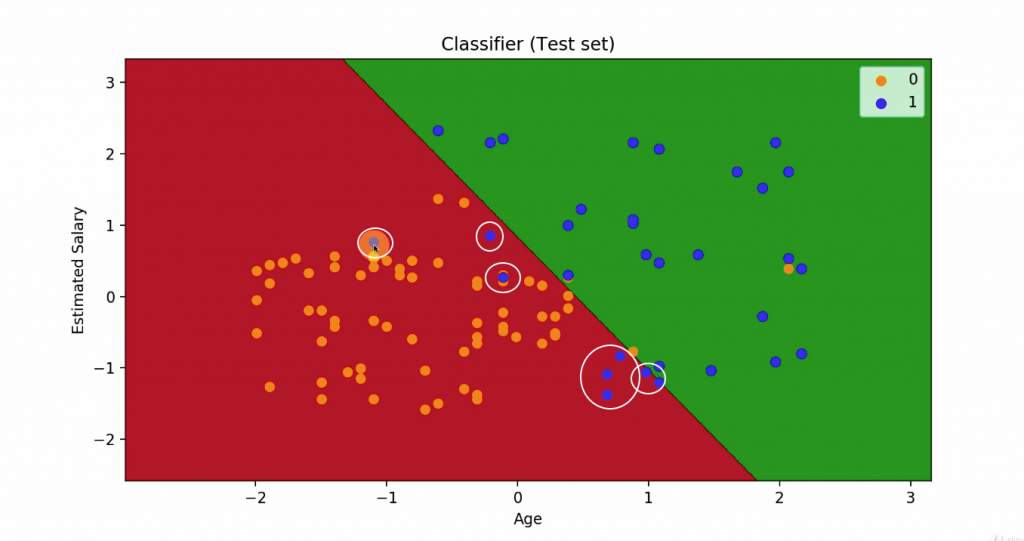

用Test set 畫出來的圖可以看到
在紅色區域有八個藍點
在藍色區域有三個橘點
因此就是前面提到的8+3個預測錯誤的點