前言

近幾年來有許多科學領域開始利用網路分析(Network Analysis)與graphical models建立不同隨機變數之間的關係，也就是利用一些節點(nodes)與線(edges)的集合形成的網路或圖形來了解複雜系統的運作機制，例如社交網路(social network)、類神經網路(neural network)與基因網路(genetic network)等。而本文關注的是描述變數之間關係的網路模型，也就是關聯性網路(association network)，屬於非監督式學習的範疇，利用機率模型找出許多解釋變數或特徵之間的相關性，並且可以將這些相關性視覺化。

Graphical Models

Graphical model是建立網路結構的其中一種方法，結合圖論與機率分佈，可以表達多個隨機變數彼此之間的關係，通常表示為G(V, E)。頂點(vertices)表示隨機變數的集合，連線(edge)表示隨機變數之間的關係。而網路模型根據圖形中連線有無方向性，可簡單分為紀錄因果關係的有向圖(directed graph)與記錄相關性的無向圖(undirected graph)，例如以下示意圖：

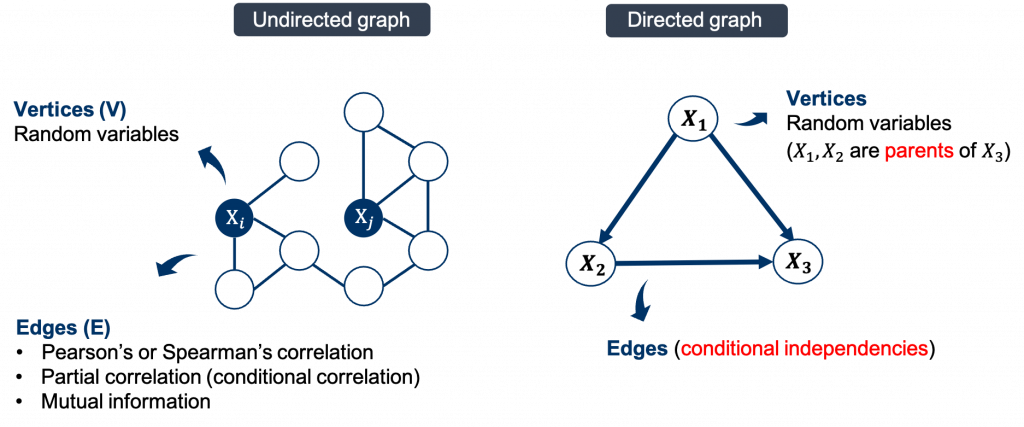
在無向圖的網路模型中，連線可以自行選擇隨機變數相關性的衡量方法，例如皮爾森相關係數(Pearson’s correlation)、斯皮爾曼等級相關係數(Spearman’s rank correlation)、肯德爾等級相關係數(Kendall’s tau rank correlation)與勝算比(odds ratio)等。還有，以熵(entropy)，來衡量兩個隨機變數Xi與Xj之間非線性關係的相互資訊(mutual information)。但上述用來定義網路中連線的方法都著重在計算兩個隨機變數之間的邊際相關(marginal association) 程度，也就是只能考慮兩個隨機變數的關係 ;對於存在多個隨機變數時，則不考慮這兩個隨機變數以外其他隨機變數的影響，這些數值沒辦法直接反映兩個隨機變數的關係。

然而，複雜的系統常常是由多個隨機變數一同參與運作，考慮變數之間直接的相關性應該也要考慮其他變數所造成的影響，因此利用兩個隨機變數的條件相關性(conditional dependence)或稱為偏相關係數(partial correlation) 來定義網路中的連線較符合這樣的情境。偏相關係數也就是在給定其他隨機變數下兩個隨機變數的相關性，也就是說這種表達方式可以討論在調控其他隨機變數之後，兩個隨機變數之間的關係；沒有連線則表示兩個隨機變數在給定其他所有變數下為條件獨立(conditional independence)。在這種定義下的無向圖模型又稱為馬可夫隨機場(Markov random field)或馬可夫網路(Markov Network)。

Gaussian Graphical model(GGM)

在馬可夫網路(Markov Network)定義下，根據隨機變數資料型態的不同，所適用的機率模型也不同，例如連續資料比較常見的有處理常態資料的Gaussian Graphical model與非常態資料的nonparanormal model，離散資料的有處理二元資料(binary data)的Ising model，以及延伸的Potts model。這些模型利用假設的機率分佈的性質來建立網路結構，今天的內容主要會介紹Gaussian Graphical model。

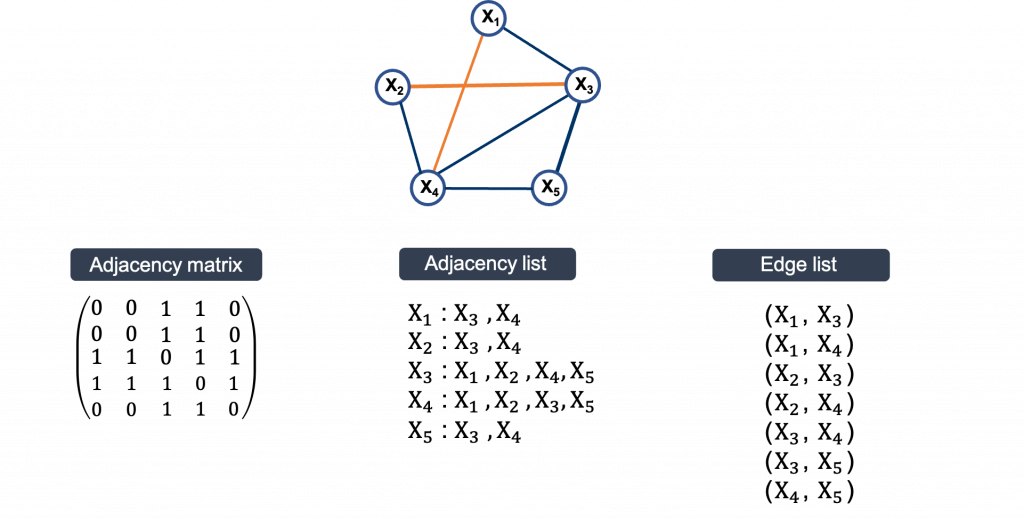
Gaussian Graphical model就是一個將資料假設服從多維度常態分配的方法，例如以下的示意圖中右邊三個節點的網路模型就是假設成三維的常態分佈。在GGM建立的網路結構是以偏相關係數(partial correlation)的數值來決定連線。如果把精確度矩陣(precision matrix)定義成共變異數矩陣的反矩陣，那麼偏相關係數就可以利用精確度矩陣的元素來計算。如同上述在無向圖的定義一樣，沒有連線表示的是條件獨立，GGM在多維度常態的假設下就可以用，partial correlation或precision matrix element是否等於零來定義有沒有連線。例如右邊網路中X2與X3沒有連線因此在precision matrix中我們就會在相對應的位置看到等於0，而X1與X2之間的partial correlation的數值可以利用公式計算。根據這些定義，GGM框架下的網路結構(network structure)就可以藉由估計偏相關係數或精確度矩陣來建立。

精確度矩陣的估計方法: Graphical Lasso

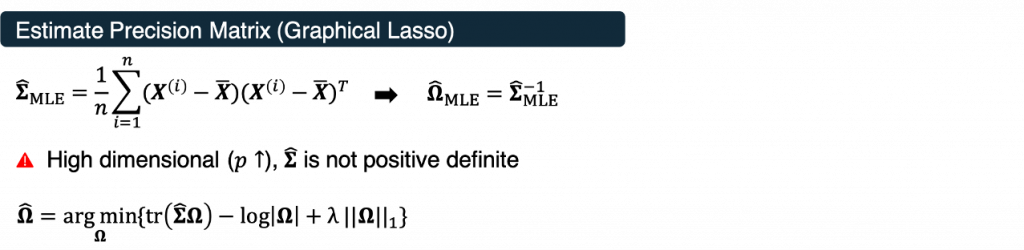
剛才有提到精確度矩陣的定義是共變異數矩陣的反矩陣，因此最直覺的想法就是計算共變異數矩陣最大概似法的估計(MLE)也就是樣本共變異數矩陣再取反矩陣得到精確度矩陣的MLE估計，不過在資料維度大於樣本數(P > n)的時候這個共變異數矩陣就不會是full rank，也就是不存在反矩陣，因此有文獻提出使用lasso penalty，也就是Graphical Lasso(GLasso) 的方式來求解，這個方法在原來MLE的求解過程中加入lasso penalty來幫助挑選變數，這裡指的變數也就是精確度矩陣的元素，使得接近0的數值被縮到0，而數值較大的可以保留，也讓網路結構有了稀疏性(sparsity)的假設。

網路結構的表示法

Python

import numpy as np
from sklearn.covariance import GraphicalLasso

true_cov = np.array([[0.7, 0.0, 0.3, 0.0],
                     [0.0, 0.4, 0.0, 0.0],
                     [0.3, 0.0, 0.3, 0.2],
                     [0.0, 0.0, 0.2, 0.8]])
                     
X = np.random.multivariate_normal(mean = [0, 0, 0, 0], 
                                  cov = true_cov, 
                                  size = 400)
cov = GraphicalLasso().fit(X)

np.around(cov.covariance_, decimals=3)
np.around(cov.location_, decimals=3)