前言

過去內容提到的Optimal Separating Hyperplane、Support Vector Classifier與LDA等方法，都是利用線性的直線或平面的方式將資料分類。但有時實際的資料並不一定能用線性的方法將資料分類，因此支持向量機(Support Vector Machine, SVM)拓展了Support Vector Classifier的概念，使SVM的模型可以處理線性方法不能處理的資料分類問題。

過去在線性迴歸中，一般的線性迴歸模型只能以解釋變數與反應變數的線性關係處理或預測資料，若想建構非線性的關係可以使用多項式迴歸(Polynomial Regression)來建構模型。也就是利用basis expansion的方法，將本來的解釋變數利用一些函數轉換到其他空間，多項式迴歸將原本解釋變數形成的空間(feature space)拓展到更高維度的空間，例如在本來的線性迴歸加上等。

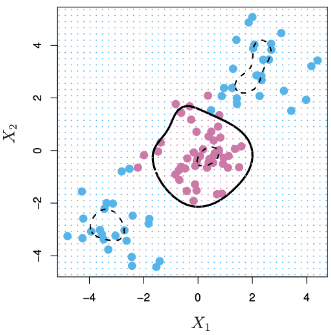
這樣的概念也可以使用到Support Vector Classifier中，原本使用的feature是建構線性的hyperplane，若利用就可以建構出非線性的hyperplane，例如以下拓展空間後的SVC。basis expansion擴展空間的方式並不局限於多項式的方法，還有其他許許多多的方式可以擴展feature space，例如與等等，雖然這樣的方法似乎很直覺也容易理解，但是可能會導致最後的計算以及估計參數的困難。支持向量機(Support Vector Machine, SVM)提供了另一種有效率的方法擴展support vector classifier使用的變數空間。

支持向量機(Support Vector Machine, SVM)

• 內積(inner product):
  

1. 在support vector classifier的求解問題中，可以利用Lagrange multipliers來估計參數，得到的係數估計為：
   
2. 因此SVC的hyperplane f(X)可以寫成:
   
3. 而上式的特性是在資料點不是支持向量(support vector)時，，假設S為收集了這些support vector的集合，因此f(x)又可以寫成：
   
4. 將上述的inner product寫成kernel function的表達式：
   
   在這個定義下的kernel function稱為linear kernel function。kernel是一個可以用來衡量兩個資料點相似程度，在內積的概念中，兩個獨立的向量在空間中互相垂直，向量的內積為0，因此kernel也是類似於這樣的概念來計算資料的相似程度。然而，kernel有許多種定義的方式，使用非線性的kernel擴展變數空間的support vector classifier就稱為支持向量機(Support Vector Machine)。

• 常見用於SVM的kernel function:

1. dth-Degree polynomial kernel:
   
2. Radial kernel:
   
3. Neural network:
   
   利用這些不同的kernel function可以建立出不同的非線性邊界或平面來將資料分類，因此不同的資料型態適合使用的kernel function也會不同，例如下圖是利用Radial kernel的結果：
   

Python建立模型

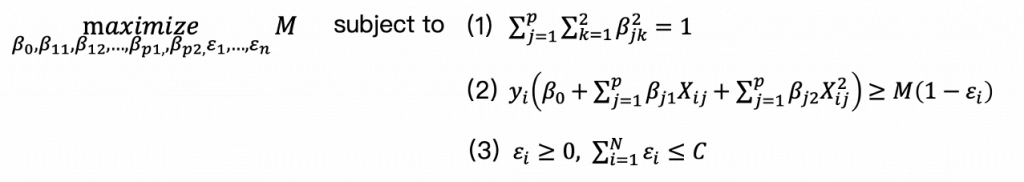
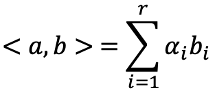
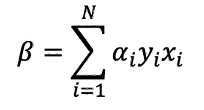
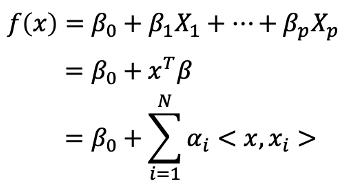
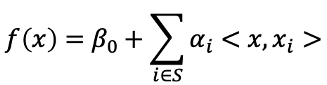
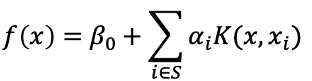
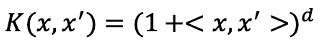
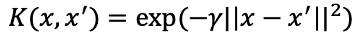
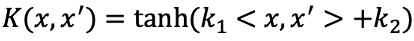
from sklearn.svm import SVC
model = SVC()
model.fit(X_train,y_train)

predictions = model.predict(X_test)

from sklearn.metrics import classification_report,confusion_matrix
print(confusion_matrix(y_test,predictions))
print(classification_report(y_test,predictions))

from sklearn.model_selection import GridSearchCV

#GridSearchCV
param_grid = {'C':[0.1,1,10,100,1000],'gamma':[1,0.1,0.01,0.001,0.0001]}
grid = GridSearchCV(estimator = SVC(),param_grid,verbose=3)

#找出表現最好的參數
grid.fit(X_train,y_train)
#顯示表現最好的參數
grid.best_params_
#顯示最佳estimator參數
grid.best_estimator_

#利用最佳參數再重新預測
grid_predictions = grid.predict(X_test)

print(confusion_matrix(y_test,predictions))
print(classification_report(y_test,grid_predictions))

參考資料與圖片來源：
An Introduction to Statistical Learning