前言

鐵人賽來到了最後兩天，其幾天的內容屬於機器學習中監督式學習(Supervised learning)的模型，這兩天將撰寫的是兩種非監督式學習(Unsupervised learning)的方法，包含主成分分析(Principal Components Analysis, PCA)與網路分析(Network Analysis)的Undirected graphical models。相比之下，非監督式學習常常作為探索式資料分析的方法，但是往往比監督式學習方法更加困難，因為沒有反應變數或outcome可以驗證得到結果的好壞。由於許多領域都需要非監督式學習的幫忙，因此這類的議題也變得越來越重要。

主成分分析(Principal Components Analysis, PCA)，指計算主成分以及使用主成分來分析資料的過程，屬於一種降低維度(dimension reductoin) 的統計方法，利用較少的變數來代表原本資料大部分的訊息。在前幾天的系列文章線性迴歸模型常見的問題中，提到當許多個解釋變數或特徵(feature)之間存在高度相關性時的共線性問題，會使估計迴歸係數的準確度降低，使其變異數變大估計較不穩定，此問題也可以利用PCA降低資料的維度保留最能代表資料的主成分，解決原本變數之間高度相關性的問題。另外，PCA也能當成將資料視覺化(visualization)與資料插補(imputation) 的工具。

主成分分析(Principal Components Analysis, PCA)

• 主要概念：將資料旋轉或投影，找到新的變數代表資料中最多的變異，且新的變數之間互相獨立。

• 例如以下的示意圖：
  將原始資料與旋轉得到的新變數與，其中將資料投影到上可以獲得代表原始資料更多的變異，而PCA利用計算變異數矩陣 的eigenvector的方式，找到投影後可以獲得最大變異的方向：
  

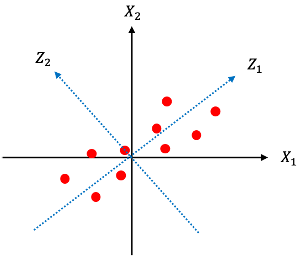
• 投影的概念：
  在系列文章線性迴歸模型中提到，線性迴歸模型就是找出最能夠描述反應變數Y的某一種X的線性組合，因此可以想成空間投影的概念，將反應變數Y投影到X構成的空間中建立的模型。而PCA也是利用投影的概念，想找到投影後具有最大變異的方向。

• 數學形式(假設資料經過標準化)：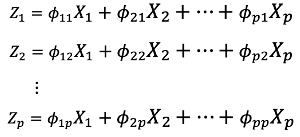
  

• 數學推導(假設資料經過標準化)：
  
  由上述的推導過程得知，可以獲得投影後變異最大的方向為共變異數矩陣 長度為1的特徵向量(eigenvector)，例如第一主成分 ，其中X係數為最大的特徵值(eigenvalue)所對應到的特徵向量(eigenvector)。

Python

import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -2], [-2, -4], [-3, -2], [1, 2], [2, 1], [3, 2]])
pca = PCA(n_components = 2)
pca.fit(X)

print(pca.explained_variance_ratio_)
print(pca.singular_values_)