前言

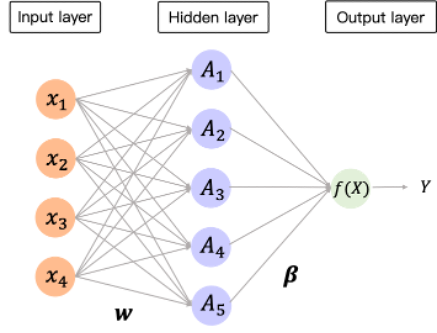
昨天介紹了Single Layer Neural network與Deep Neural Network，而模型的結構在隱藏層(hidden layer)越來越多時，看似比過去提到的模型要複雜許多，因此如何估計其中包含的參數(也就是每層之間的權重weight)將是一個重要的問題，昨天提到處理迴歸問題的loss function可以使用squared error loss，而處理分類問題時可以使用cross-entropy loss，今天將會簡單的描述Single Layer Neural network中迴歸問題估計參數的方法。

Single Layer Neural network

• 示意圖(假設p = 4，選擇五個activation k = 5):
  
• 估計(類似非線性最小平方法的問題):
  
• 以上的估計方式看起來與線性迴歸模型利用最小平方法估計參數類似，但是在神經網路這樣的架構下，參數有一個巢狀結構，且此估計式並不是凸函數(convex function)，無法直接利用微分的方式來尋找最小值。因此，在Neural Network常利用迭代的方式，也就是梯度下降法(Gradient descent)。
• Gradient Descent:
  

1. 由一個猜測的起始值 開始進行迭代(t=0)
2. 持續進行迭代直到 不再減少。

• 例如以下的示意圖，非convex function，因此圖形中可能有不止一個最佳解，而Gradient descent就能以迭代的方式解決此問題：
  

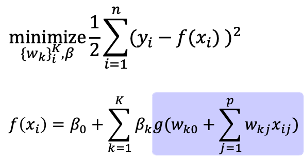
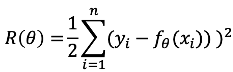
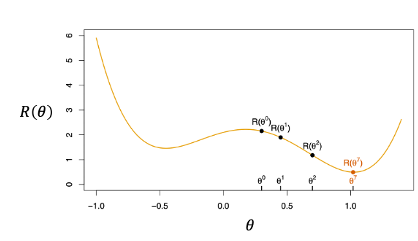
在 的梯度(Gradient)，或稱為偏導數(Partial Derivatives)，表示使 沿著 增加最快的方向，因此在此處我們希望將沿著該方向的相反方向來找處可以使 達到最小值。例如：

• 計算 的梯度(Gradient)：
  

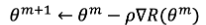
可以發現最後用來進行參數迭代的兩個式子中都包含了殘差(residual)， ，等於最後的配飾值(fitted value)與觀察值的差異某些程度上決定了模型中的參數估計值，因此這種估計方式稱為反向傳播法(Backpropagation)。以上是neural network最簡單結構的參數估計方式，不過隱藏層更多且更複雜的模型利用到的方式大方向也是如此，甚至可以利用迴歸模型中加上正規化(regularizatoin)的方式，在估計式中加入懲罰項，可以處理overfitting的問題。

Python

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential()
# 加入第一層(input layer)，10個節點，與input shape 13 element vector (1D).
model.add(Dense(10, input_shape=(13,), activation='relu'))
# 加入第二層(hidden layer)，10個節點
model.add(Dense(10, activation='relu'))
# 加入第三層(output layer)，1個節點
model.add(Dense(1))

小結

到目前為止，這個系列文章也介紹的許多機器學習中常見的模型，以及這兩天介紹的深度學習的模型，此時會面臨到的問題是：若幾個模型可以處理某個特定的問題時，應該選擇哪個模型？與像是黑盒子的深度學習模型相比，線性迴歸模型(Linear regression)、支持向量機(SVM)與隨機森林(Random forest)等方法，更簡單並且容易呈現以及理解。當這些方法表現都差不多時，選擇簡單的模型方便使用者做解釋以及理解，因此有了強大的深度學習後，仍可以在處理資料時嘗試使用這些簡單的模型。

參考資料與圖片來源：
An Introduction to Statistical Learning