破題

這道題目中的平衡二元樹定義為：二元樹中每個節點的左右子樹高度差的絕對值不超過1。根據定義，一棵二元樹是平衡二元樹，當且僅當其所有子樹也都是平衡二元樹。因此，我們可以使用遞迴的方式判斷二元樹是否為平衡二元樹。遞迴的順序可以是 top-down 或 bottom-up。這種方法可以幫助我們更容易理解如何判斷一棵二元樹是否為平衡二元樹。

不再孤軍奮戰，一起準備面試吧！
在投遞履歷前，先找人幫你 review 通常會是蠻好的一個方式。 履歷諮詢會從技術主管的視角切入，根據你的個人經歷，優化整體的履歷脈絡。 搭配簡潔專業的排版會讓你的履歷表變得更加出色。別再猶豫了，動動手指投遞履歷吧！
立即加入 Line 讀書會，和大家一起為面試做好準備！

履歷諮詢	加入讀書會 (邀請碼：2830)

Top-down 遞迴

解題思路

具體方法是類似於二元樹的前序排序：對於當前造訪到的節點，首先計算左右子樹的高度，然後判斷左右子樹的高度差是否不超過 。如果符合條件，則分別遞迴地造訪左右子節點，並判斷左子樹和右子樹是否平衡。這是一個 top-down 的遞迴過程。這種方法可以幫助我們更容易理解如何判斷一棵二元樹是否為平衡二元樹。

程式

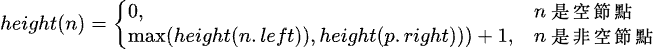
import kotlin.math.abs
import kotlin.math.max

class Solution {
    fun isBalanced(root: TreeNode?): Boolean {
        val result = traverse(root)
        return result.second
    }

    private fun traverse(root: TreeNode?): Pair<Int, Boolean> {
        return root?.let {
            if (it.left == null && it.right == null) {
                1 to true
            } else {
                val leftResult = it.left?.let { traverse(it) } ?: (0 to true)
                val rightResult = it.right?.let { traverse(it) } ?: (0 to true)
                1 + max(leftResult.first, rightResult.first) to
                        (leftResult.second && rightResult.second && abs(leftResult.first - rightResult.first) <= 1)
            }
        } ?: (0 to true)
    }
}

複雜度分析

• 時間複雜度:
  ，其中 是二元樹中的節點個數。在最壞情況下，二元樹是完美二元樹，需要造訪所有節點，時間複雜度為 。對於節點 ，如果它的高度是 ，則 traverse(p) 最多會被呼叫 次（因為節點 的每一個祖先節點都必須先被造訪）。在平均情況下，一棵樹的高度 滿足 ，因為 ，所以總時間複雜度為 。但在最壞情況下，二元樹形成歪斜結構，高度為 ，此時總時間複雜度為 。

• 空間複雜度:
  ，其中 是二元樹中的節點個數。空間複雜度主要取決於遞迴呼叫的層數，遞迴呼叫的層數不會超過 。

　更多 LeetCode 解答在此，一起來學習！

不再孤軍奮戰，一起準備面試吧！

從技術主管的視角切入，根據你的個人經歷，優化履歷脈絡

履歷諮詢	加入讀書會 (邀請碼：2830)