接下來要進入到 VAE 的重頭戲，數學原理的解釋與推導

其實從前兩天的文章應該已經能瞭解 VAE 如何運作、有什麼特點，如果真的很排斥數學，好像可以先左轉離開（欸？？？

不過多認識一些數學原理，也能深化對 VAE 的認識，那就開始今天的內容吧～

VAE 的數學原理

（iThome 的 Markdown 好像不支援 math expression，傷眼抱歉）

生成模型的學習原理大致來說就是學習出一個接近真實影像分布的生成分布，再從這個分布抽樣，產生新的影像。而 VAE 的出發點是用類似 Gaussian Mixture Model 的概念來估測真實影像的分布。

至於什麼是 Gaussian Mixture Model 呢？簡單來說就是我們能用很多個 Gaussian distributions 的疊合來近似各種複雜的分布～以下圖為例，實線為待估測的分布，我們就可以用三個 Gaussian distributions 來近似它。

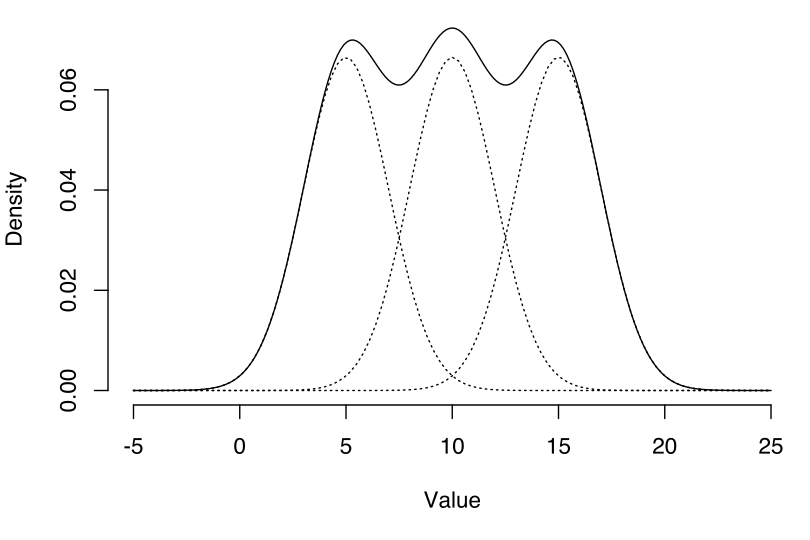
（圖片來源：Gaussian-mixture-example.svg）

回到 VAE 的學習目標，我們需要估計出真實影像的機率分布 p(x)，利用連續性的 Gaussian Mixture Model 的概念，我們可以用無限多個 Gaussian distributions 疊合以估計複雜的真實影像分布 p(x)。

首先從 normal distribution 抽樣得到 z，每個 z 代表不同的 Gaussian distributions：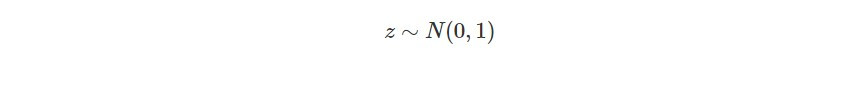

z 會決定 Gaussian distribution 的平均數 μ(z) 和標準差 σ(z)，因此可以定義一個 Gaussian distribution，以下就是給定 z 的情況下隨機變數 x 的機率分布：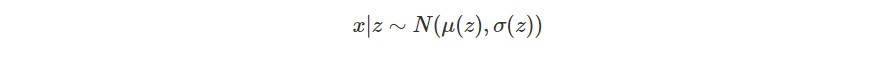

按照不同 Gaussian distributions 出現的機率將其疊合（也就是對 z 積分）即可得到 p(x)：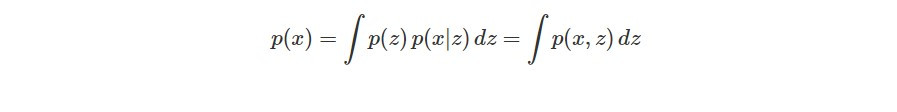

p(z) 即為 standard normal distribution，p(x|z) 則是 N(μ(z), σ(z))，然而 μ(z) 和 σ(z) 也是待估計的，而且積分通常計算困難。

我們也可以將 p(x) 透過條件機率的公式寫成：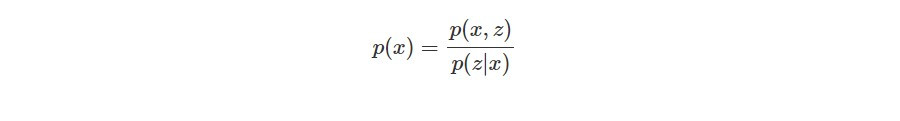

然而後驗機率 p(z|x)（給定一張影像 x，code z 的機率分布）也是未知。後驗機率難以計算的問題相當經典，可以透過 variational inference 的方法解決，也就是以簡單的分布 q(z|x)（可以自己定義）近似難以計算的 p(z|x)。此外，為了估計最有可能的 p(x)，我們要最大化觀測資料 x 的 log likelihood：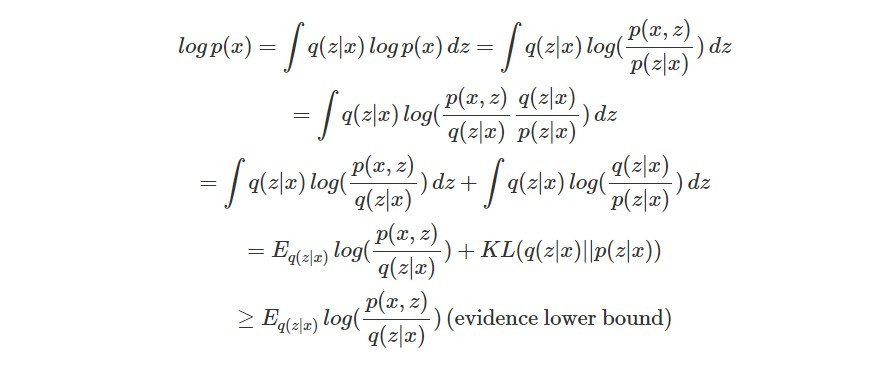

之前說明過，KL divergence 是兩個機率分布相似程度的度量，由於它的值是非負數（大於等於 0），所以前項會是 log p(x) 的 lower bound。又由於 log p(x) 被稱為 evidence（因為 log p(x) 是我們為資料選擇好的 model 的 evidence），所以該項就被稱為 evidence lower bound (ELBO)。而我們要提高 ELBO，並降低 q(z|x) 和 p(z|x) 的 KL divergence，也就是找到最能近似真實分布 p(z|x) 的 q(z|x)。

而 ELBO 又能繼續改寫如下：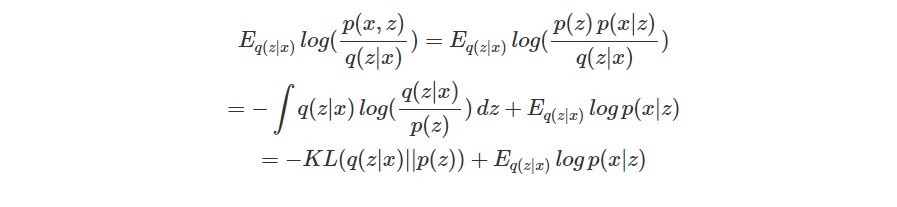

其中第二項代表的就是在 encoder 是 q(z|x) 的情況下，給定 code z 得到觀測影像 x 的 log likelihood 期望值，其實就是評估 VAE 還原的影像和輸入影像是否一致的 reconstruction likelihood。

而除了讓輸出和輸入影像接近，我們還必須最小化 KL(q(z|x)||p(z))（讓 q(z|x) 和 normal distribution p(z) 接近）：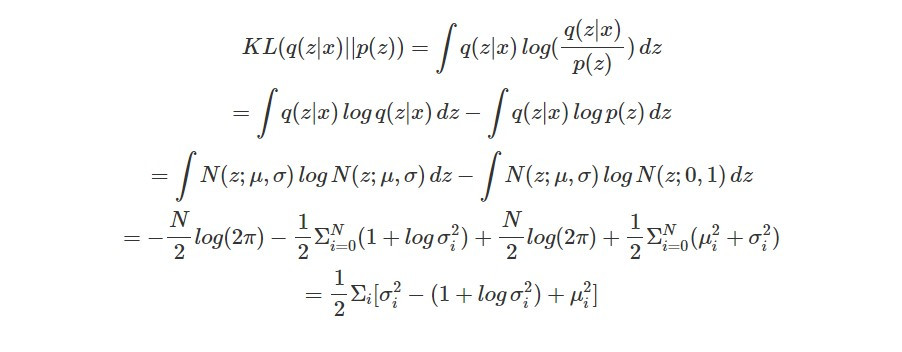

這就是昨天介紹 VAE 的第二個學習目標的數學形式，之前提供的直觀解釋是為了避免 VAE 學習到的 Gaussian distributions 的標準差為 0 並加上 L2 regularization，而今天則推導了背後的數學原理～

參考資料

• 李宏毅老師的線上影片ML Lecture 18: Unsupervised Learning - Deep Generative Model (Part II)
• Variational auto-encoder paper Auto-Encoding Variational Bayes