一、 介紹

邊緣檢測就像是影像處理中的「找輪廓」技術，類似於用筆劃描繪物體外形的概念。這個方法在很多情況下都非常有用，它可以幫助我們找出物體的邊界，進而瞭解物體的形狀和輪廓。

這項技術在許多實際應用中發揮著重要作用，就像下圖所示。例如，當我們希望讓電腦能夠「看見」照片中的拼圖時，邊緣檢測能夠協助電腦識別出拼圖的外形。同樣地，這項技術在醫學影像分析、行人或車輛識別等情境中也扮演著關鍵的角色。

攝影師：Pixabay: https://www.pexels.com/zh-tw/photo/269399/

二、 原理

1. 梯度(Gradient)

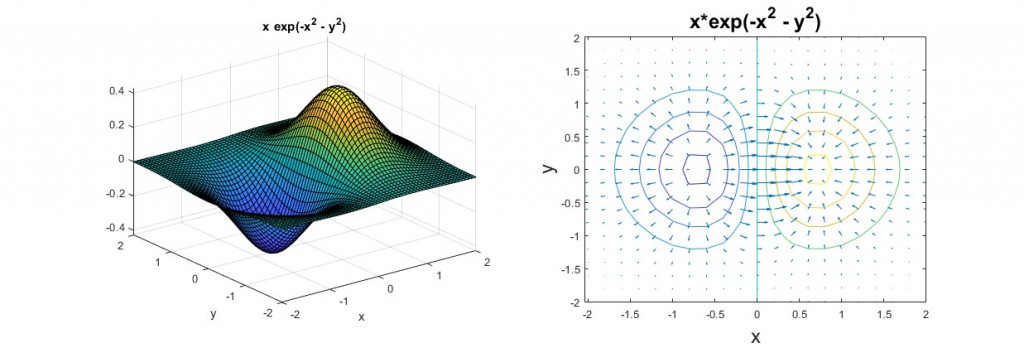
在數學和物理學領域，「梯度」是一個重要的概念，它用來描繪變化率和方向之間的關係。梯度是一個向量，可以提供函數在不同方向上變化的速率(斜率)和趨勢。這個概念在多個學科中均有廣泛應用，在影像處理中，梯度可以用來檢測影像的明暗變化率，相當於做一階微分，變化越強的位置越有可能是邊緣。下圖是一個函數f(x,y)3D圖和f(x,y)的梯度圖，可以看到箭頭的大小和方向就代表了這個函數f(x,y)變化的強度和趨勢。

假設你要求出f(x,y)的梯度，數學是可以表示為：

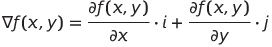
其中，X和Y的偏微分可以表示為：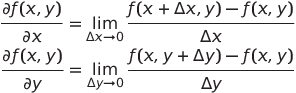

可以看到，其實梯度做的就是分別對f(x,y)做x、y的偏微分並加上單位向量i、j，也就是求出f(x,y)的斜率。

想像你正在爬一座山谷，而你目前處在左邊x為0.7的谷底，而你所在的位置可以用一個高度函數f(x,y)來表示，這個函數會告訴你在不同x、y位置的海拔高度。現在，你想找到一條最快的路徑，從山谷爬到山頂，而梯度就是你在這個情況下的指南針。

梯度告訴你在哪個方向上上升得最快，或者說在哪個方向上海拔增加最快。如果你想迅速爬上山頂，你會選擇朝著梯度最大(也就是箭頭最長)的方向前進，因為這是上升最快的方向。這個梯度方向就是你要找的最快路徑，而梯度的大小則表示了爬升的速度。

2. 什麼是邊緣

「邊緣」指的是影像中強度或顏色突然劇變的地方，通常這些地方代表著物體或結構的界限。這些邊緣是影像中值得關注的區域，因為它們反映了物體之間的分界，進一步協助我們進行物體辨識、分割以及其他相關的電腦視覺應用。

下圖是一張黑白相接圖。假設我們將y座標設為0，並將相鄰的點的灰階值分別表示為f(x,0)、f(x+1,0)和f(x-1,0)。可以注意到，f(x,0) 就是這張影像的邊緣，因為f(x-1,0) 的灰階值為0，而f(x+1,0) 的灰階值為255，兩者之間具有極大的灰階值差異。這種劇變提示著可能存在物體的邊界，這是邊緣檢測的基本觀念。

3. 邊緣檢測

在邊緣檢測中，「梯度」被用來表示影像中強度變化的情況。劇烈的變化通常隱含著物體的邊緣或輪廓。我們通常會在影像的每個像素位置計算梯度，以瞭解影像不同區域的變化。

邊緣檢測的核心概念是計算影像f(x,y)在不同方向上的梯度，也就是是計算影像的一階導數 f'(x,y)求出特定座標處影像灰階值的變化率。由於影像f(x,y)的離散性質，我們可以將上文的梯度計算公式中的變化量Δx和Δy替換為1。這樣一來，我們就能夠計算出影像f(x,y)在不同方向上的一階導數。這種方法使我們能夠捕捉到影像中的強度變化，從而識別出潛在的邊緣區域。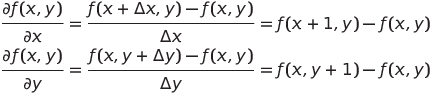

我們計算影像在特定座標點的 x 方向和 y 方向上的強度變化率，將其平方後相加，然後取平方根，以獲得這個向量的大小。這個梯度大小可以告訴我們影像在這個位置的強度變化有多大，從而有助於我們識別出邊緣或其他重要的特徵。第二個公式是對梯度大小的一個近似表示。它通過將x、y的梯度的絕對值相加，然後除以 2 來近似計算梯度的大小，雖然近似公式的精確度較低，但它可以作為一種快速估算的方法，特別是在需要快速處理大量影像數據時。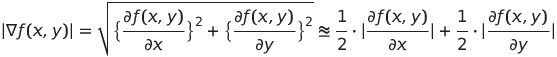

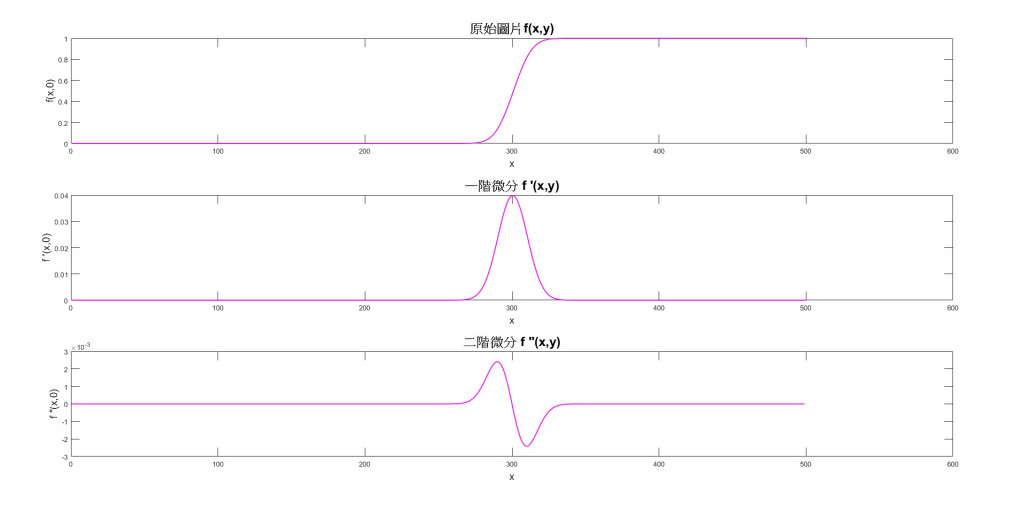
f(x,y)是一張有極大差距的原始灰階圖，f(x,y)是每個x座標對應的灰階值，分別對原始灰階圖進行一次微分和二次微分。

1. 原始影像 f(x,y)：第一個子圖展示了原始影像 f(x,y)。這個函數代表x從0到500的灰階值f(x,0)，黑色轉變為白色的像素值。
2. 一階微分 f'(x,y)：第二個子圖展示了原始影像 f(x,y)的一階導數，即影像函數的灰階值變化。這個圖呈現了原始影像在不同 x 值處灰階值的變化情況。
3. 二階微分 f''(x,y)：第三個子圖展示了原始影像 f(x,y) 的二階導數，代表一階微分的變化率。這個子圖顯示了一階微分的變化情況，也就是影像的斜率變化的速率。當二階微分的值為正時，表示變化的速率正在增加；當二階微分的值為負時，表示變化的速率正在減小。

透過這三張圖，我們可以觀察到一些有趣的現象。在一階微分f'(x,y)的圖中，最高點恰好對應著原始影像f(x,y)的邊緣位置。這表示在邊緣位置，影像的強度變化最劇烈。而在二階微分f"(x,y)的圖中，我們可以看到邊緣的存在對應著零點交叉 ( Zero-crossing ) 的情形。所謂零點交叉是指，某個數值變化的區域從正值轉變為負值，這種變化可能是邊緣的一個特徵。