• 今天我們要進入unsupervised learning的範圍了，這類型的資料通常有一個特色，就是資料量龐大，類別沒有標籤target，無法使用趨勢分析（regression）或是分類分析來解決的範疇。

• 假設您現在要分析影響新竹房價的原因，考慮影響房價的種種原因（特徵x）：例如：居民的平均收入，交通便利（是否有捷運），大型企業的比例（台積電是否設廠），治安是否良好，居民的教育程度，附近的嫌惡設施，是否有許多公園，人口老化程度，新生兒出生率...等因素。這些就是我們在day16所說的特徵x_1，x_2，....。現在問題來了，面對龐大的特徵x，固然我們可以使用散點圖scatter plot，判斷與房價target y是否有相關性，但是人工判斷難免會有誤差，如果能交由機器（電腦）自動幫我們判斷，既可免去人工誤差，自動化的選擇特徵，又幫我們省下不少時間。

• 接下來要談的是：


• PCA的原理

• PCA的步驟

• PCA的程式碼


• PCA的原理：

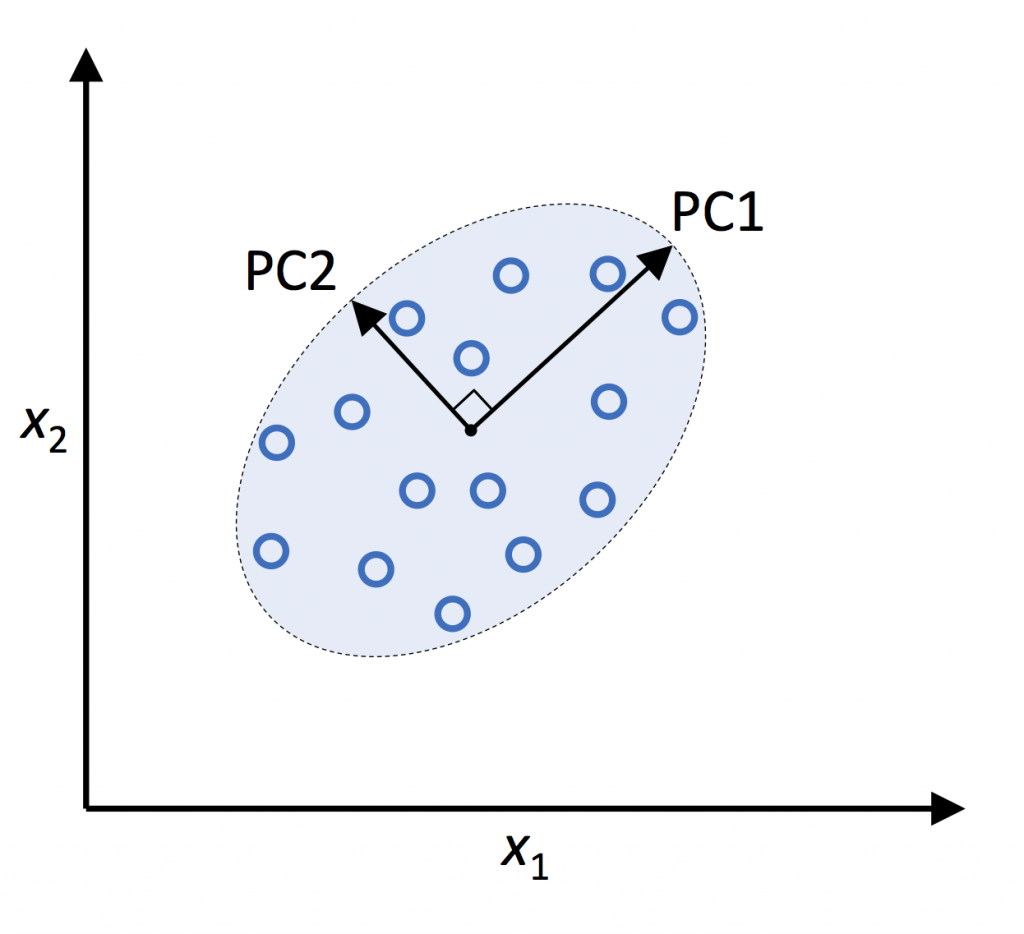
其原理就是將高維d的特徵資料投影映射到k維空間，這k維正交特徵就是主成份。PCA就是從原始的空間中按遞減順序找一組相互正交的座標軸。取前幾大正交軸做所取的PCA。正交就是互相垂直的意思。投影映射就像是day17所說的將資料放到高維資料，在從高維空間取出hyperplan，最後在投影回二維空間中的「投影」，不熟悉的同學，可以翻一下[day17]（https://ithelp.ithome.com.tw/articles/10347436) 的圖片。


• PCA的步驟：

1.標準化d維數據集
2.建立成對特徵的共變異數矩陣
3.分解「共變異數矩陣」為特徵向量與特徵值
4.遞減排序特徵向量與特徵值
5.選取前k個特徵向量成投影矩陣
6.將投影矩陣映射到新k維特徵子空間
7.新的k維子空間的正交軸就是主成份

• 共變異數矩陣：
• 

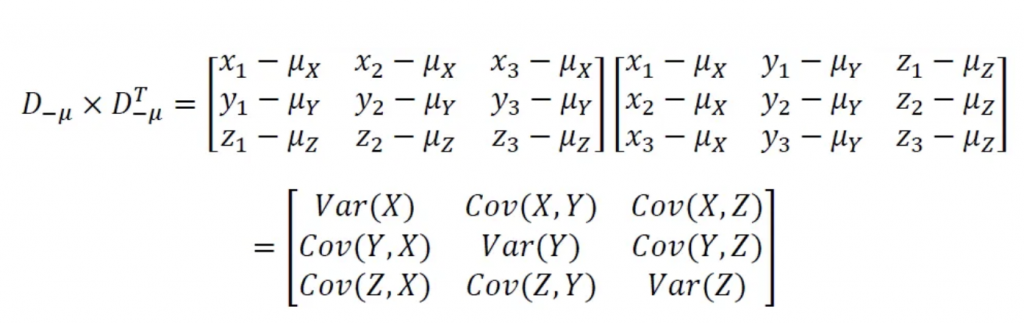
圖片參考關於共變異數有詳細的介紹，因偏向統計學，同學可以參考這篇，寫得很詳細。

• 第3點此處的特徵向量與特徵值是線性代數所說的特徵向量與特徵值。

• PCA的程式碼：

• 接下來我們以logistic regression為程式範例碼：


from sklearn.decomposition import PCA
// 載入PCA模型
pca = PCA(n_components=2)
// 訓練資料pca降維轉換，注意是fit_transform
X_train_pca = pca.fit_transform(X_train)
// 測試資料pca降維轉換
X_test_pca  = pca.fit(X_test)

• 取n_components = 2，表示只取前兩大的pc1 與 pc2。
  

這系列結束後，我將繼續挑戰IT鐵人30日：
佛心分享 ： it 考照之路
主題：從摸索7個月到下定決心訂下3週後考試：自學取得PMP 3AT 執照

• 明天我們將要談分群法：K-means，Hirarchy Clustering，DBSCAN，敬請期待。