架構設計

延續前幾篇的設計模式，我們的目標是模組化演算法，提供一個生成演算法的工廠，並且把使用方法封裝在 update 和 render 方法中，這裡，物件的初始化是動態的，所以我們採用較自由的建構函式而非 Class：

export default function createAlgorithm(){
    //......
    this.update = () => {
        this.步驟1();
        this.步驟2();
        this.步驟3();
    }
    this.render = () => {
        //......
    }
    return this;
}

掠食者獵物模型

這個模型是一個簡單的微分方程式，在二維平面上 XY 分別代表了捕食者和獵物的數量，然後，針對每一個點，都存在一個切線方向，指出演化的方向。捕食者跟獵物之間的關係是互相依賴的，故此微分方程用於描述牠們的此消彼長，特色是沿著中心點呈現漩渦紋理。

公式

獵物方程：
掠食者方程：

在這個圖形中，XY的值域是 0~1 所以要先將座標映射，再還原：

this.equation1 = (x, y) => {
	return this.alpha * x - this.beta * x * y;
}
this.equation2 = (x, y) => {
    return this.delta * x * y -  this.gamma * y;
}
this.addTexture = (width, height, ctx) => {
    //......
    const ex = x / width;
    const ey = y / height;
    const dx = this.equation1(ex, ey) * width;
    const dy = this.equation2(ex, ey) * height;
    //......
}

addTexture：本質上，我們是拿該方程式計算切線，並當作圖形的紋理做使用。

隨機點生成

沿著中心點外圍的一個圓形區域，要如何產生均勻密度的隨機點呢？若想深入這個問題，這會牽涉到一點數學和統計學，我推薦這個外國人的影片作為參考。

讓我們實作其中一種穩定高效的隨機點生成方法，用極座標來生成：

"d": Math.sqrt(Math.random()) * width, // distance
"r": Math.random() * 2 * Math.PI, // radian

現在，我們可以初始化 2000 個點

this.reset = (width, height) => {
    const len = 2000;
    this.data = [];
    for (let i = 0; i < len; i++) {
        const point = {
            "d": Math.sqrt(Math.random()) * width / 2, // distance
            "r": Math.random() * 2 * Math.PI, // radian
        };
        point.x = width / 2 + point.d * Math.cos(point.r);
        point.y = height / 2 + point.d * Math.sin(point.r);
        this.data.push(point);
    }
}

• ES6 擁有更簡潔的替代方案，但會犧牲可讀性：
• new Array(2000).fill(null).map(() => {})
• Array.from({ length: 2000 }, () => {})

動畫

我們可以嘗試讓它動起來，配合這個圖形的特色，讓所有點隨著中心點旋轉：

this.motion = (width, height) => {
    this.data.forEach((point) => {
		const rad = this.transitionRadian;
        point.x = width / 2 + d * Math.cos(point.r + rad);
        point.y = height / 2 + d * Math.sin(point.r + rad);
    })
}

OK，僅僅旋轉看起來很單調，因此我們嘗試加入一些變換，讓 cos 和 sin 相乘：

this.motion = (width, height) => {
    this.data.forEach((point) => {
		const rad = this.transitionRadian;
        point.x = width / 2 + d * Math.cos(point.r + rad) * Math.sin(point.r + rad);
        point.y = height / 2 + d * Math.sin(point.r + rad);
    })
}

現在我們得到一個沙漏！？

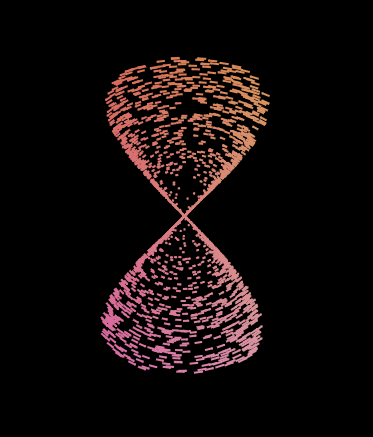
進一步，我們可以多套一層三角函式來計算週期，從而實現變速的來回旋轉：

this.motion = (width, height) => {
    this.data.forEach((point) => {
		const rad = this.transitionRadian;
        const period1 = Math.cos(rad);
        point.x = width / 2 + d * Math.cos(point.r + period1) * Math.sin(point.r + period1);
        point.y = height / 2 + d * Math.sin(point.r + period1);
    })
}

接著，為了使整個圖形更具動感，我們提供 XY 座標不同的週期，扭轉整個圖形：

this.motion = (width, height) => {
    this.data.forEach((point) => {
		const rad = this.transitionRadian;
        const period1 = Math.cos(rad)*Math.sin(rad);
        const period2 = Math.sin(rad);
        point.x = width / 2 + d * Math.cos(point.r + period1) * Math.sin(point.r + period1);
        point.y = height / 2 + d * Math.sin(point.r + period2);
    })
}

沙漏好像在旋轉，坍塌成了......一個幸運餅乾!?

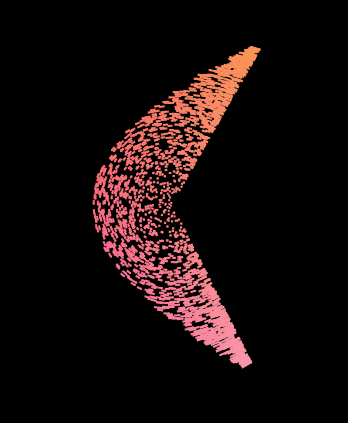
最後，我們試著把距離乘上週期，離中心點越遠的點的變換速度會更快。最後的座標計算則改回基本的極座標公式，這樣的圖形會有對稱性：

this.motion = (width, height) => {
    this.data.forEach((point) => {
        const rad = this.transitionRadian;
        const period1 = Math.cos(rad);
        const period2 = Math.sin(rad);

        const angular1 = point.d * period1 * 0.1;
        const angular2 = point.d * period2 * 0.1;
        
        point.r+= Math.PI / 1000;

        point.x = width / 2 + d * Math.cos(point.r + angular1);
        point.y = height / 2 + d * Math.sin(point.r + angular2);
    })
}

point.d * 0.1：距離越遠，變換速度越快。0.1是一個常數
angular1, angular2：我們的後置參數現在是處理圖形變換，不再處理普通的旋轉
point.r：在角度上提供一個基本的旋轉

還不錯，現在我們拿到了一些芋頭：

物理意義說明：

• Period (週期)：在物理學中，週期是指完成一個完整循環所需的時間。在我們的動畫中，週期可以影響點的旋轉速度與位置變化的頻率。具體來說，週期越短，點的旋轉速度越快，顯示出更頻繁的運動變化。這種變化可以用於創造更為豐富的視覺效果，使動畫更具動感。

• Angular Velocity (角速度)：角速度是描述物體沿著圓周運動的速度，通常以弧度每秒（rad/s）來表示。在我們的程式碼中，Angular 並不表示角速度，但由於它是乘以距離所得，具備和角速度相同的特性，故以此命名。

結論

在本篇文章中，我們探討了如何設計一個基於掠食者與獵物模型的模組化動畫系統。透過這個系統，我們不僅實現了隨機點生成，還成功地將這些點以富有創意的方式動起來，形成了視覺上引人入勝的效果。

在動畫的過程中，我們利用了數學中的三角函式以及物理學中的週期和角速度概念，使得每個點的運動不再是簡單的旋轉，而是形成了更為複雜和動態的圖形。未來，我們可以進一步探索不同的數學模型與物理原理，來豐富動畫的效果和多樣性。

美中不足的就是它是一種視覺暫留的錯覺，只有圖片是不夠展示的，感興趣的話，請玩玩看：
LokaVolterra