"回歸診斷"，其實這是個我很有興趣的命題，但很無奈學校沒教，我也不知道要去哪裡才能學到這些知識，診斷是第一步，重要的是第二步，準診斷之後如何更正確的建立模型。問過現在在台灣唸研究所的同學也沒有答案...，摁...我想，如果真的想成為統計研究員，在台灣應該是沒有機會了。

講是這樣講啦！雖然我不會修正模型，但是診斷模型好像也是可以試試看，從常態性檢定開始吧！
(資料都是這次的計程車營運狀況調查)

library(car)
qqPlot(fit,labels=row.names(states),id.method="identify",simulate=TRUE,main="Q-Q Plot")

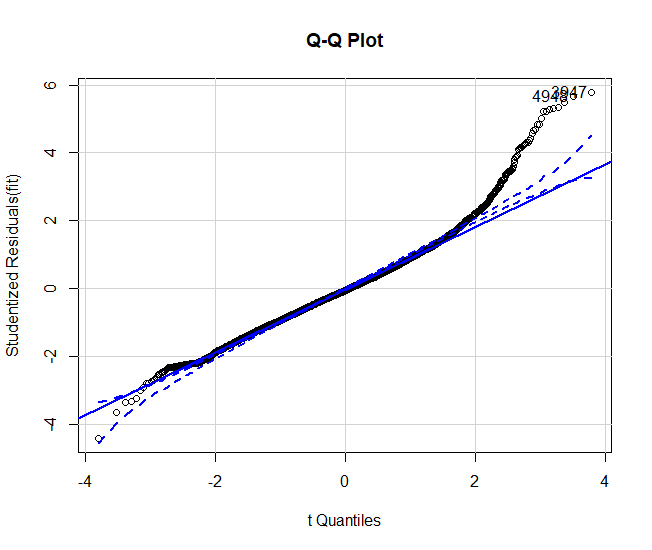
這個問題困擾我很久了，就是..這張圖統計系人人都會畫，但是這張圖畫完接下來呢？

我在網路上找到一篇文章，他的方法值得我效尤，不知道這張圖要怎麼看嗎？很簡單，把各種狀況都畫出來不就好了嗎？看自己畫出來的圖跟常態、偏態、高低狹的圖做比較，就能判斷自己的殘差事屬於哪種類型。(別人的程式碼我就不上了，下面會有參考網址)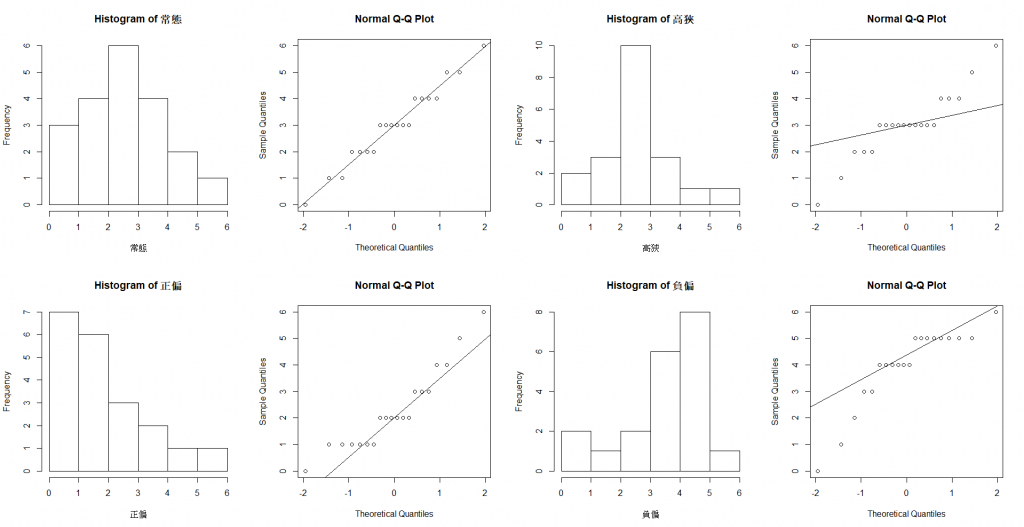

硬要說的話比較偏向正偏吧！但其實是很接近常態分佈了。

Q-Q plot：常態機率圖,是一種能看出資料分布情形,是否符合常態分配的圖.
橫軸顯示的是理論分位數,縱軸則是樣本分位數,資料點散佈於圖上,並有一條虛擬的常態線通過.

資料參考：https://read01.com/PjzReP.html#.W8xIefYzaUn
資料參考：https://www.surfacewalker.com/single-post/2017/03/22/R-language-%E5%B8%B8%E6%85%8BQ-Q%E5%9C%96normal-Q-Q-plot%E7%B0%A1%E4%BB%8B%E8%88%87%E7%B9%AA%E8%A3%BD

如果繪製student-殘差圖，這筆資料是真的還挺不錯，常態部分沒什麼需要修正的。
殘差值:（真實值-預測值）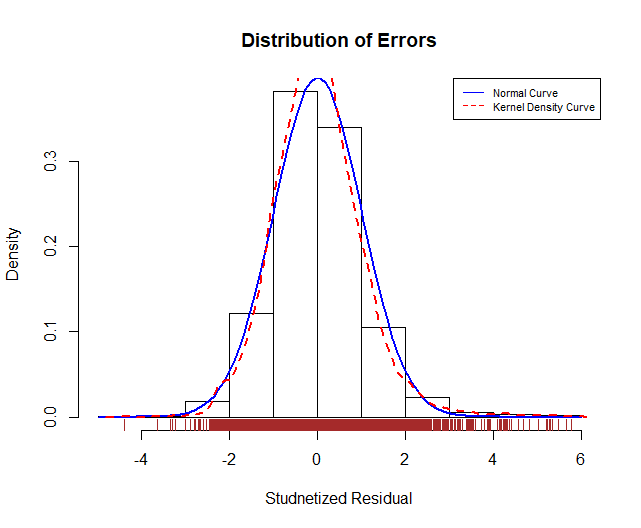

residplot<-function(fit,nbreaks=10){
  z<-rstudent(fit)
  hist(z,breaks=nbreaks,freq=FALSE,
       xlab="Studnetized Residual",
       main="Distribution of Errors")
  rug(jitter(z),col="brown")
  curve(dnorm(x,mean=mean(z),sd=sd(z)),
        add=TRUE,col="blue",lwd=2)
  lines(density(z)$x,density(z)$y,
        col="red",lwd=2,lty=2)
  legend("topright",
          legend=c("Normal Curve","Kernel Density Curve"),
          lty=1:2,col=c("blue","red"),cex=0.7)}
residplot(fit)