資料+統計+演算法，我們稱為機器學習，如何不斷修正統計模型，達到更好的預測，便是數據分析師的工作。
我們確保的一件事情，數據越多，我們就能做出更好的預測。因此模型不是建立就好，更重要的是確保模型的正確性以及預測能力。

fit<-lm(一天營業總收入~.,data=xx)
summary(fit)

Residual standard error: 595.5
這是RMSE，是回歸分析上的一種指標，計算殘差的標準差，越小值代表使用模型預估出來的預測值和實際值的誤差越小，越接近真實情況，此模型的特性是會對數值中的特異值會有比較大的放大效果，這東西的數值不見得有意義，通常是用來比較兩個模型的好與壞。

R^2: 0.3189, Adjusted R^2: 0.3122
在回歸分析上R^2也是很好的指標，R^2代表迴歸能夠解釋的變數，最大值為1，與RMSE不同的是被標準化過了，可以看出能夠解釋幾 %的資料(以我的回歸來說，只能解釋3成多一點的資料，這...其實是好事啦，表示我後面有很多修正空間)。R^2在Excel有內建，非常方便。(有興趣可以找找很簡單的，而且在excel裡甚至要做次方、指數回歸線的討論都很簡單，唯一的缺點就是excel有資料筆數限制吧，然後跑比較慢，要不然我其實大多時間也是尻excel在做這件事)

shapiro.test(fit$residual[1:5000])

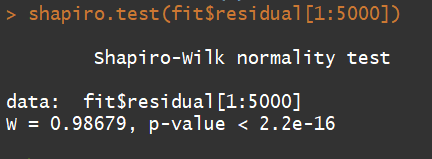
由於虛無假設H0:殘差服從常態分配，因為p-value < 0.05，代表拒絕H0。
這是我後來找到檢測是否為常態分配的方法，不過有個限制就是數據不能超過5000筆。那很顯然，我的數據並沒有通過殘差服從常態分配，我其實也是很無所謂的，本來就希望沒通過，藉由這次鐵人賽找到通過的辦法

library(car)
durbinWatsonTest(fit) 

由於虛無假設H0:殘差間相互獨立，因為p-value < 0.05，代表拒絕H0。 雖然一樣沒通過，至少我找到檢驗的辦法了。

ncvTest(model)

由於虛無假設H0:殘差變異數具有同質性，因為p-value < 0.05，代表拒絕H0。(這表示上面的線性模型無法使用)

參考資料：https://read01.com/PjzReP.html#.W81bwnszaUl