前言

我們昨天提到一些關於蒙地卡羅方法的介紹，我們可以知道蒙地卡羅是一種透過重複大量試驗，逼近數值的方法。那麼，要怎麼把這個方法用於估計價值函數呢？

價值估計

重複試驗對象

昨天在估計 的時候，我們使用「面積比例」這個方式估算，因為面積與 有關。因此在估計價值函數時，也需要找與價值函數有關，且可以使用大量試驗獲得數值，數學家看上的是回饋這個數值。

之前在討論獎勵函數時，我們給了這樣的定義：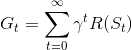

這裡的 指的是從現在這個狀態，到整個過程結束時，我們可以獲得的回饋。用 GridWorld 為例子做說明，假設我們現在在狀態 1，移動到終點 (即「整個過程結束」) 的狀態轉移情況可能有：

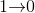
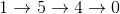
還有許多 族繁不及備載 的情況，這邊些只列出兩個，方便等一下說明。

連結回饋與價值函數

事實上，透過數學定義，我們就可以將獎勵與價值函數牽扯上關係，定義如下：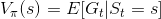

看起來有點熟悉，又不太確定在哪裡看過嗎？沒錯，因為我們之前在動態規劃方法時，只看了這個式子一眼，就把它拆成遞迴的形式了。

這個定義的形式出現在 Day 5

好的，我們繼續。在動態規劃方法時，我們透過遞迴形式逼近價值函數。而現在，我們透過重複試驗，真的取得許多 ，現在我們只需要取平均即可。繼續使用上面 GridWorld 的例子，假設 = 0.9，則

• 
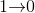
  可以得到 = -1

• 
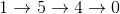
  可以得到 = -1 -0.9 -0.81 - 0 = -2.71

那麼現在在狀態 1 ，我們計算出的狀態價值即為 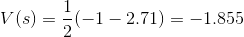，只要繼續上述的過程，就可以取得更多的試驗結果，更精確的估計狀態價值。