前言

上一篇，我們完成了手寫阿拉伯數字的辨識，但同時也留下很多的問題：

1. 為什麼模型要設成兩層完全連接層(Dense)?
2. 為什麼第一層完全連接層(Dense)要設為 128?
3. activation function、優化器(optimizer)、損失函數(loss)、效能衡量指標(metrics) 要如何選擇?
4. 為什麼使用小畫家，寫0~9實際測試，準確率好像不如測試資料那麼高? 我寫9，永遠辨識錯誤，唉 !
5. 使用像素辨識，好像不是很高明，應該用輪廓或線條比較好吧。
6. 如果要辨識多個數字，例如車牌，要怎麼作?
7. 如果要辨識其他事物，怎麼作?

我們就一一來作探討，並對模型及參數作一些實驗，看看超參數(Hyperparameters)對效能的影響。

為什麼模型要設成兩層完全連接層(Dense)?

理論上，越多層表示有越多的迴歸線組合，預測應該越準確。加兩對 Dense/Dropout 實驗一下，：

# 建立模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  
  # 加兩對 Dense/Dropout
  tf.keras.layers.Dense(64, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(16, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  
  tf.keras.layers.Dense(10, activation='softmax')
])

完整程式請參考 04_01_More_Dense.ipynb。

參數總量從101,770 增加至 109,946個，結果準確率從 0.9743 增加至 0.9676，只有一點點的增加。再確認一次，改用另一個資料集 Fashion_MNIST，它包含女人10個用品如下：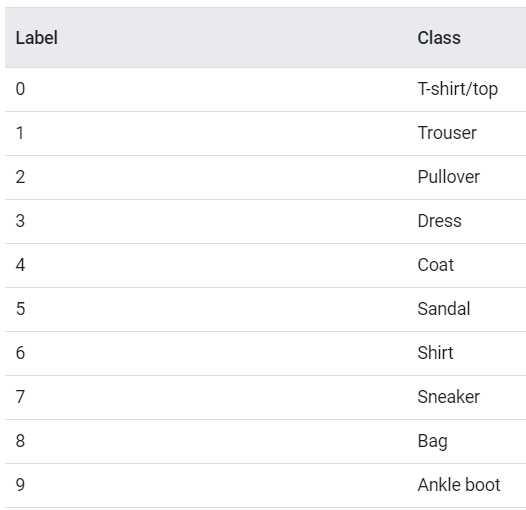

圖一. Fashion MNIST 10個類別(Classes)

修改前面資料載入的程式碼如下：

# 匯入 Fashion MNIST 女人10個用品 訓練資料
(x_train, y_train),(x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()

其他程式碼均相同，完整程式請參考 04_02_More_Dense_Fashion_mnist.ipynb。結果準確率從 0.8629 增加至 0.8655，只有一點點的增加。

為什麼第一層完全連接層(Dense)要設為 128?

理論上，越多神經元表示迴歸線的特徵數越多，預測應該越準確。分別將神經元個數設為 32/128/512 ：

  tf.keras.layers.Dense(32, activation='relu'),  
  
  tf.keras.layers.Dense(128, activation='relu'),
  
  tf.keras.layers.Dense(512, activation='relu'),
  

完整程式請參考 04_03_change_neural_count.ipynb。
準確率分別為 0.8534、0.8691、0.8652，有趣的事發生了，神經元個數越多，準確率並沒有越高。

為什麼執行週期(Epoch)要設為 5?

執行週期(Epoch)是指所有資料作一次正向傳導及反向傳導，理論上，執行週期(Epoch)越多次預測應該越準確。分別將epochs設為 5/10/20 ：

# 訓練
history = model.fit(x_train_norm, y_train, epochs=5, validation_split=0.2)

history = model.fit(x_train_norm, y_train, epochs=10, validation_split=0.2)

history = model.fit(x_train_norm, y_train, epochs=20, validation_split=0.2)
  

完整程式請參考 04_04_change_epoch.ipynb。
準確率分別為 0.8686、0.8825、0.8851，執行週期(Epoch)越多次，準確率確實越高，但可能會造成過度擬合。

activation function、優化器(optimizer)、損失函數(loss)、效能衡量指標(metrics) 要如何選擇?

1. activation function 有很多種，可參考【維基百科】，可參考中間的表格，包括公式及機率密度函數。早期隱藏層的activation function 大都採取 Sigmoid 函數，但近年發現使用 ReLU，效果比較好。Tensorflow 支援的activation function 可參考【這裡】。範例請參考 04_04_activation_function.ipynb，例如，sigmoid介於 (0,1)，tanh介於 (-1,1)，各有各的應用時機。

2. 優化器(optimizer) 有很多種如下，可參考【這裡】。

• SGD
• RMSprop
• Adam
• Adadelta
• Adagrad
• Adamax
• Nadam
• Ftrl

優化器主要是學習率(learning rate)的控制，採固定速率，優化求解的時間需時較久，如果採動態調整速率，剛開始加大學習率，等到接近最佳解時，就逐漸縮小學習率，優化求解的效率就可以提高了。另一方面，可以跳過局部最佳解(Local Minimum)或馬鞍點(Saddle Point, 如下圖)，找到可能的全局最佳解(Global Minimum)。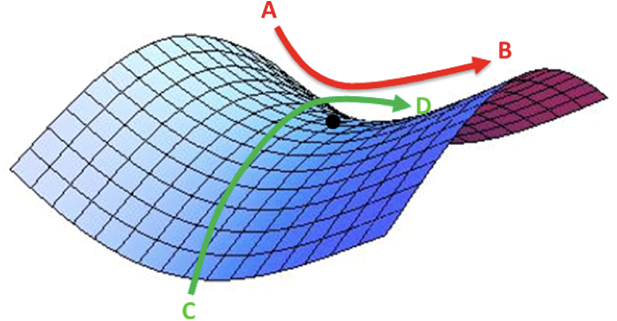

圖二. 馬鞍點(Saddle Point)，圖形來源：『Neural Network Optimization』

一般而言，Adam 優化器可以表現得很好。『Neural Network Optimization』 有很詳細的介紹。

3. 損失函數(loss)的介紹，可參考【這裡】。
   損失函數牽涉到優化求解的收斂的效率，常用的損失函數有均方誤差(Mean Squared Erro, MSE)、交叉熵(Cross entropy)，也可以自訂損失函數，這很重要，很多演算法都是自訂損失函數，產生各種耀眼的成果，例如風格轉換或GAN。

4. 效能衡量指標(metrics)的介紹，可參考【這裡】。除了準確率(accuracy)外，還包括AUC、Precsion、Recall...等，可在不同的情況下選用，例如，二分類、多分類或不平衡樣本(Imbalanced data)等。

再提醒一下，可參照下圖，以上參數是優化過程所需的設定。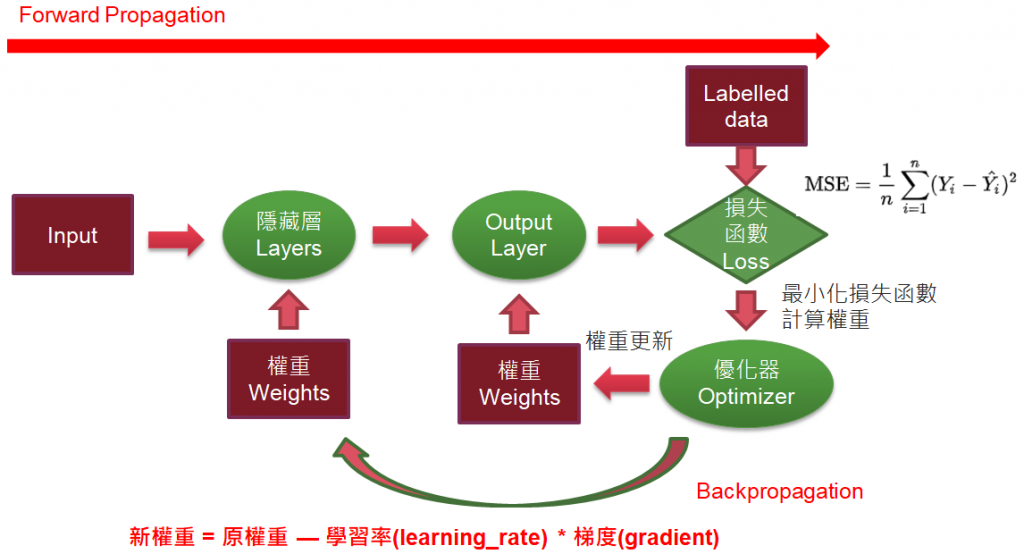

圖三. 優化過程

效能調校(Performance Tuning)的技巧

從以上的說明，有太多參數組合可以選擇，如何找到最佳參數值? 不幸的消息是沒有準則，神經網路還是黑箱科學，只能靠經驗與實驗，上述的實驗其實不太客觀，因為載入資料及訓練時會作隨機抽樣，因此，每次執行結果都會不同，因此，正式來作的話，應該採取【交叉驗證】(K-Fold cross validation)比較客觀。

筆者因為撰稿的壓力，偷懶一下，引用【Deep Learning with TensorFlow 2 and Keras】一書的實驗。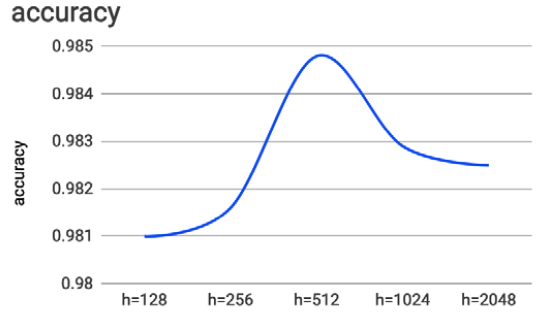

圖四. 神經元個數對準確率的影響，並不是越多越準

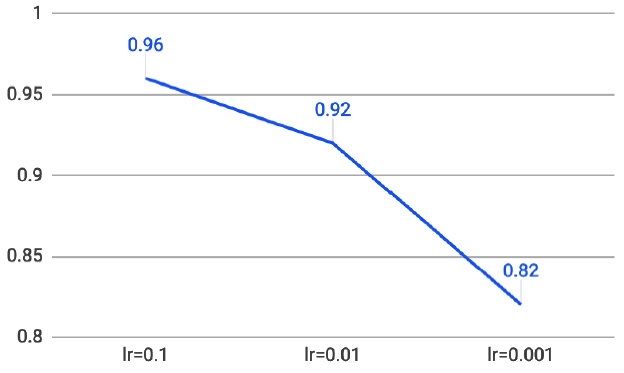
圖五. 學習率越大，準確率越高，對此結論存疑

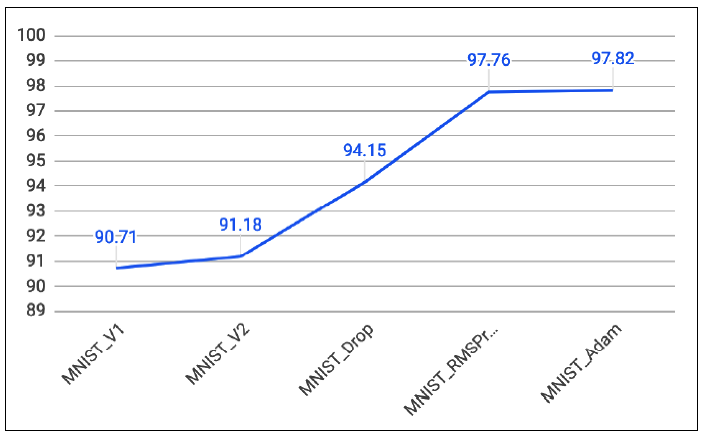
圖六. 優化器與Dropout對準確率的影響

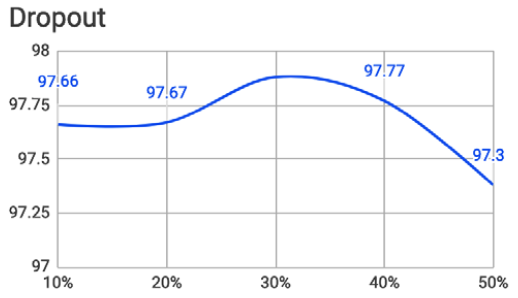
圖七. Dropout比例對準確率的影響

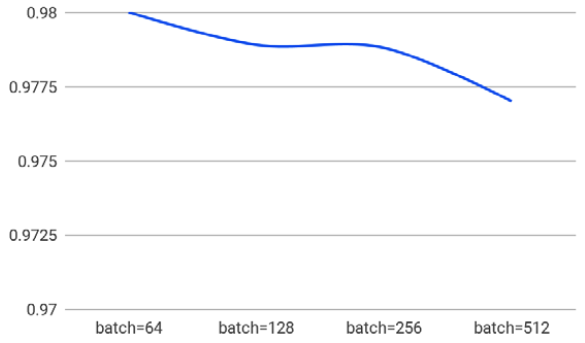
圖八. 批次大小(batch size)對準確率的影響

批次大小(batch size)是訓練時可設定的參數，是指訓練多少樣本更新一次權重。

# 訓練
history = model.fit(x_train_norm, y_train, epochs=5, validation_split=0.2, batch_size=800)

結論就是所有的參數並不是越大越好，當參數值過大時，準確率有可能反而下降，所以，還是要針對專案作各種的實驗才是王道。

下一篇我們將繼續作效能調校，介紹如何使用 Scikit-Learn 的 GridSearchCV 函數，找到最佳參數。

本篇範例如下，可自【這裡】下載。

1. 04_01_More_Dense.ipynb
2. 04_02_More_Dense_Fashion_mnist.ipynb
3. 04_03_change_neural_count.ipynb
4. 04_04_change_epoch.ipynb
5. 04_05_activation_function.ipynb