當資料中有很多的變數時,我們不能直接將所有變數代入模型中,這可能會產生許多問題。舉例來說:
⇒ 這時候我們可能就需要去進行變數選擇 (Variable Selection)!
變數太多的解決方法包含:
- Subset Selection 子集
- Shrinkage 收縮
- Dimension reduction 降維
等等。
子集法簡單來說就是將變數們進行排列組合,組成了許多的模型後,我們再利用的衡量指標(Criteria)去決定哪種模型組成最適合。
常見的子集法有 Best Subset Selection和 Sequential variable selection(包含Forward 、Backward、Stepwise selection) 。
首先會挑選出與反應變數(Y)最相關的解釋變數(X)建構「一個模型」,再依據衡量指標去增加/去除一個變數進入模型,重複添加/移除具有貢獻度的變數,直到該模型的衡量指標數值是最佳的為止。
常使用的模型衡量指標(Criteria): AIC 、 BIC (SBC) 、 (Mallows’ C) 。以上這些衡量指標越小代表模型越適合。
⇒ [注意]模型的分配假設是正確的時,這些衡量指標才會是一個用來篩選變數的適當指標。
R code, Forward Stepwise Selection示範:
使用 Hitters Data 作為示範,這是1986 到 1987 賽季的美國職業棒球大聯盟數據。我們可以觀察什麼是影響薪資(千 美元)的重要因素。
## 讀取Hitters Data,並進行資料處裡,清除遺失值
library(ISLR2) # 載入ISLR2 套件,以讀取Hitters Data
data(Hitters) # Data Hitters is from package"ISLR2"
View(Hitters) # 觀察資料
names(Hitters) # Variables in Hitters data set
dim(Hitters) # 322 rows, 20 Variables,
Hitters<- na.omit(Hitters) # Removes missing values
sum(is.na(Hitters)) # Check no missing values
dim(Hitters) # After removing: 263 rows.
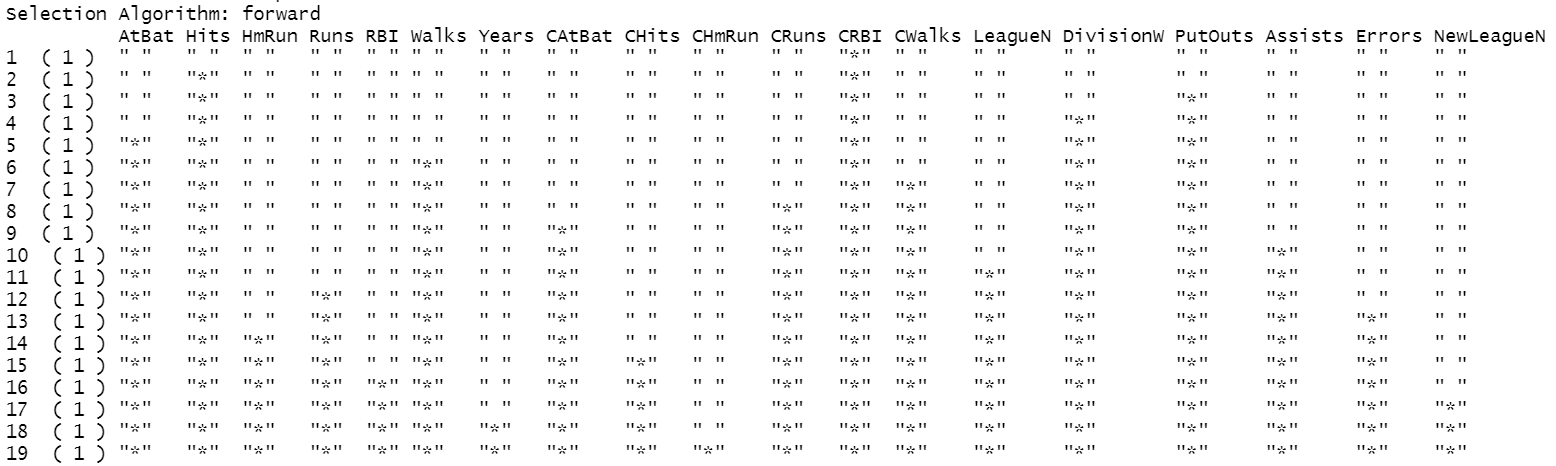
這邊以Forward Stepwise Selection,以 BIC 為模型衡量指標做示範:
install.packages("leaps") # regsubsets()
library (leaps)
regfit.fwd <- regsubsets (Salary ~ ., data = Hitters ,
nvmax = 19, # nvmax:變數數目 #共20個變數,去除目標(反應)變數,剩餘19個變數。
method = "forward") # method:"forward", "backward", "both"(逐步stepwise)
summary (regfit.fwd) # 觀察每次模型的變數選擇
summary(regfit.fwd)$bic # 每個新增變數的新模型的衡量指標BIC值
逐步增加變數時,BIC數值變化: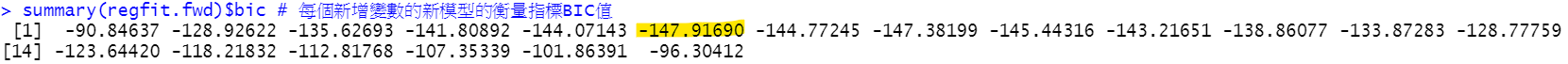
## 選出最適合的模型
regsumm<-summary(regfit.fwd)
which.min(regsumm$bic) # 想知道第幾步的模型,有最小的 BIC 值(最佳的衡量指標數值)
# 得知第六個模型最適合
coef(regfit.fwd ,6) # 觀察模型6內含的變數以及各變數的估計係數值

最終應當選擇的模型6:
lm(Salary~ AtBat + Hits + Walks + CRBI + DivisionW + PutOuts, data=Hitters)
## Other regression model accuracy metrics (取得其他最佳的衡量指標數值)
regsumm<-summary(regfit.fwd)
which.min(regsumm$cp) # 最小的cp
which.min(regsumm$bic) # 最小的bic
which.max(regsumm$rsq) # 最大的 r-squared
which.max(regsumm$adjr2) # 最大的adjusted r-squared
收縮法和子集法不同,建立回歸模型時會一口氣將所有變數放入模型中,在顧忌係數時才去進行係數的收縮。
收縮法是使用收縮係數(正則化 regularization )的方式,限制模型的複雜度,幫助我們去解決多重共線性的變數造成估計係數變異數很大的問題。
原始的係數估計是藉由 minimize RSS 去估計係數。
而 Ridge 和 LASSO regression 則是在 minimize 時,增加懲罰項(shrinkage penalty),再進行係數的估計。
RSS: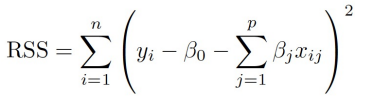
Ridge regression: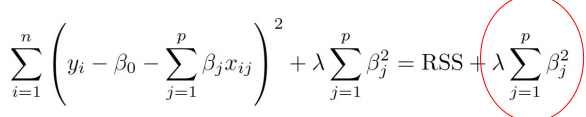
LASSO regression: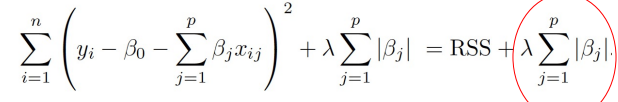
Elastic net (結合LASSO和Ridge的作法):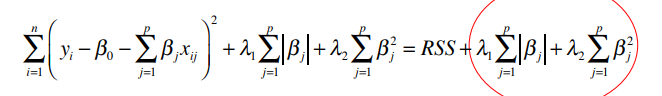
數學式可行解域的關係: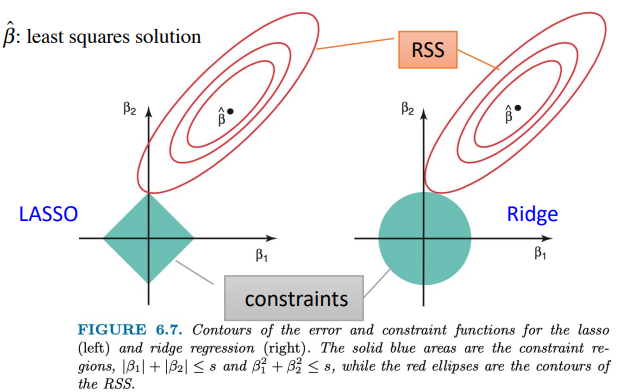
紅色是求最小值區域,而藍色是條件區域。
限制條件區域比較示意圖: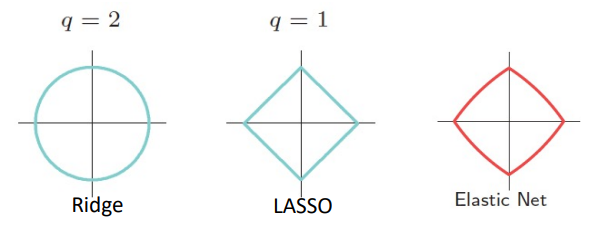
收縮法的 Regularized regression 多了一個懲罰項( lambda )的出現,所以在選擇模型時,我們還要進行Tuning parameter lambda 的步驟。
Lasso 的變數係數會陸續變為 0;但 Ridge 卻不一樣,直到某個瞬間才會全部一起變成 0。
Ridge 可以縮小係數的值,但因為 lambda 不可能為無窮大,所以係數不會等於0。Lasso的回歸係數則可以為0,如果一組變數高度相關,Lasso回歸會選擇其中的一個變數,然後把其他的都變為0。
Elastic Net 結合以上兩者,優勢是能夠比 Lasso regression 穩定,然後也能進行變數篩選。在多個有共線性的變數中,Lasso 迴歸只會選擇其中的一個變數,但ElasticNet迴歸會選擇兩個。
R code, Regularized regression示範:
Lasso ,設定alpha = 1
Ridge ,設定alpha = 0
Elastic Net ,設定 0 < alpha < 1
示範 Lasso regression 挑選變數:
install.packages("glmnet")
library(glmnet) ## 用glmnet()建立基本的Lasso模型
x <-model.matrix(Salary~.-1,data=Hitters) # Matrix, without "Salary"
y <- Hitters$Salary
## 用glmnet()建立基本的Lasso模型
set.seed(1)
train=sample(1:nrow(x),nrow(x)/2)
test=(-train)
y.test=y[test]
grid<-10^seq(10, -2,length = 100)
lasso.mod<-glmnet (x[train, ], y[train],alpha = 1, # Lasso:alpha=1
lambda = grid)
plot(lasso.mod, xvar='lambda', main="Lasso")
圖中是 lambda 值對應各變數的估計係數值。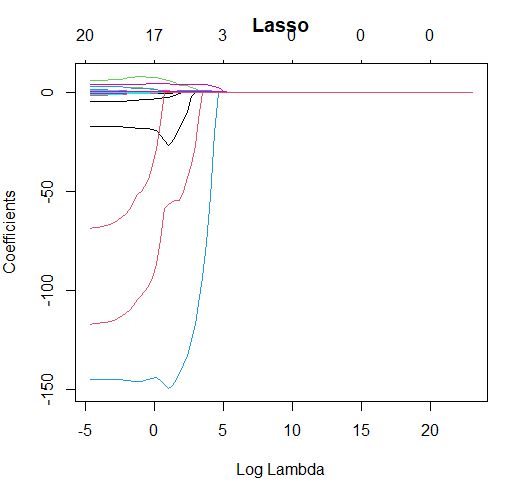
接著要找出最佳的懲罰值best.lambda (對應到最小的 Maen Square Error):
## 用cv.glmnet()找出最佳的懲罰值best.lambda
set.seed (1)
cv.out <- cv.glmnet (x[train , ], y[train], alpha = 1)
plot (cv.out)
bestlam <- cv.out$lambda.min # 評估每個模型的 cvm(mean cross-validated error),
# 取最小 cvm 模型所對應的 lambda
lasso.pred <- predict (lasso.mod , s = bestlam ,
newx = x[test , ])
mean ((lasso.pred - y.test)^2) #MSE
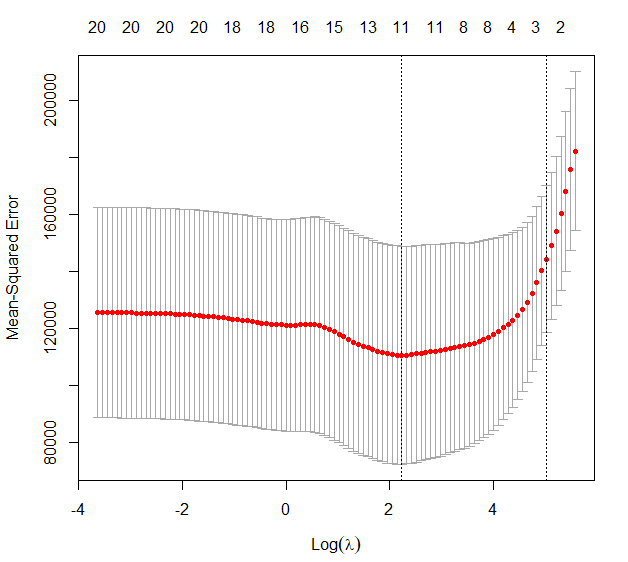
最後觀察哪些變數被挑選出來:
## 觀察哪些變數被挑選出來(係數不為0的那些)
out <- glmnet (x, y, alpha = 1, lambda = grid)
lasso.coef <- predict (out , type = "coefficients",
s = bestlam)[1:20, ]
lasso.coef
lasso.coef[lasso.coef != 0]
> lasso.coef[lasso.coef != 0]
(Intercept) AtBat Hits Walks Years
21.16991349 -0.05496356 2.18035916 2.29191347 -0.33807980
CHmRun CRuns CRBI LeagueA LeagueN
0.02823953 0.21628179 0.41713002 -19.89840766 0.38839481
DivisionW PutOuts Errors
-116.16743953 0.23752233 -0.85637833
最後決定的模型:
lm(Salary~ AtBat + Hits + Walks+ Years + CHmRun + CRuns + CRBI + LeagueA + LeagueN + DivisionW + PutOuts +Errors ,data=Hitters)
[注意]
⇒ lasso.coef 的係數不可以直接當成迴歸模型的估計係數值,必須將這些篩選出的係數重新配適迴歸模型,計算出正確的估計係數數值。
[補充]我們也可以觀察一下不同 Shrinkage Methods的係數收縮表現: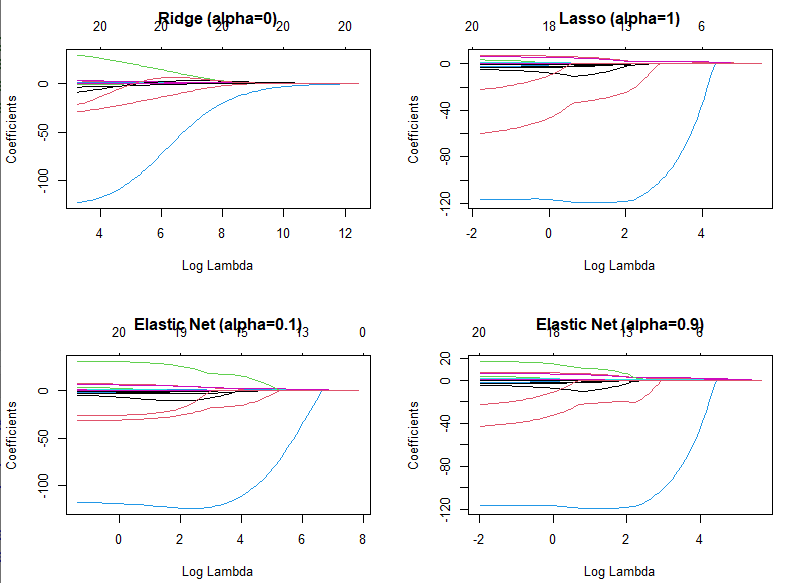
fit.ridge =glmnet(x,y,alpha=0) # Ridge-Ression
fit.lasso =glmnet(x,y) # Lasso
fit.elnet1=glmnet(x,y,alpha=0.1) # 1. Elastic Net
fit.elnet9=glmnet(x,y,alpha=0.9) # 2. Elastic Net
par(mfrow=c(2,2))
plot(fit.ridge ,xvar="lambda",main="Ridge (alpha=0)")
plot(fit.lasso ,xvar="lambda",main="Lasso (alpha=1)")
plot(fit.elnet1,xvar="lambda",main="Elastic Net (alpha=0.1)")
plot(fit.elnet9,xvar="lambda",main="Elastic Net (alpha=0.9)")
統計與機器學習 Statistical and Machine Learning 課程, 王彥雯 老師.
R筆記 – (18) Subsets & Shrinkage Regression (Stepwise & Lasso) (@skydome20 @Jeff Hung)
https://rpubs.com/skydome20/R-Note18-Subsets_Shrinkage_Methods
讀者提問:多元迴歸分析的變數選擇(@David Huang)
https://taweihuang.hpd.io/2016/09/12/%E8%AE%80%E8%80%85%E6%8F%90%E5%95%8F%EF%BC%9A%E5%A4%9A%E5%85%83%E8%BF%B4%E6%AD%B8%E5%88%86%E6%9E%90%E7%9A%84%E8%AE%8A%E6%95%B8%E9%81%B8%E6%93%87/
這7種回歸分析方法,資料分析師必須掌握!
https://www.finereport.com/tw/data-analysis/7-huigui-ff.html
An Introduction to Statistical Learning with Applications in R. 2nd edition. (2021). Springer. James, G., Witten, D., Hastie, T., and Tibshirani, R.
The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edition.(2016). Springer.Hastie, T., Tibshirani, R. and Friedman, J.
