今日大綱

• 微分
• 積分

微積分 (Calculus)是由微分 (Differentiation)與積分 (Integration)所組成的，而這兩個互為逆運算。

微分

微分所計算的是函數上某個點的斜率 (Slope)或梯度 (Gradient)，及變化的速度，而二次為分為加速度。
假設一條線其公式為y=2x+5，其斜率為2，代表每增加x一單位，y將會上升2單位，5則為截距 (intercept)。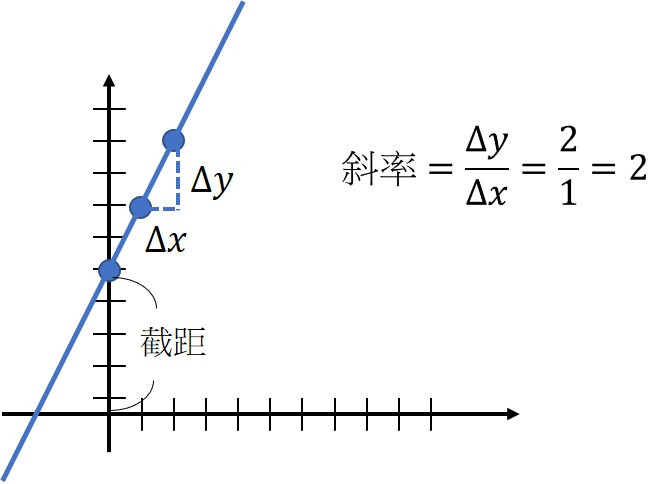

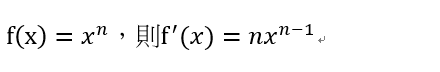
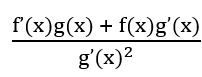
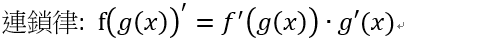
微分公式

• f(x)一階導數的表示法為f'(x)或 dy/dx
• 若f(x) = k，且k為常數，則f’(x) = 0。
• 設c為常數，若f(x)可微分，且f(x)=cg(x)，那f’(x) = cg’(x)
• 
• 設f(x)與g(x)皆為可微分函數，且h(x) = f(x) + g(x)，則h’(x) = f’(x) + g’(x)
• 設f(x)與g(x)皆為可微分函數，且h(x) = f(x) * g(x)，則h’(x) = f’(x)g(x) + f(x)g’(x)
• 設f(x)與g(x)皆為可微分函數，且h(x) = f(x) / g(x)，則h’(x) =
  
• 

偏微分 (Partial differentiation)

在機器學習與深度學習的方法中常使用偏微分，計算每個特徵的梯度，進一步計算最佳的權重。梯度與斜率的概念相似，差別在斜率為單一變數的變化量，梯度為多個變數的斜率。

梯度下降法 (Gradient Descent)就是利用偏微分，計算每個變數的梯度，讓函數沿著特定的方向前進，找出最佳解。

積分

積分計算的是長度、面積或是體積，它也可以計算累積機率密度函數 (Probability density function, PDF)。
積分常見的數學表示式如下: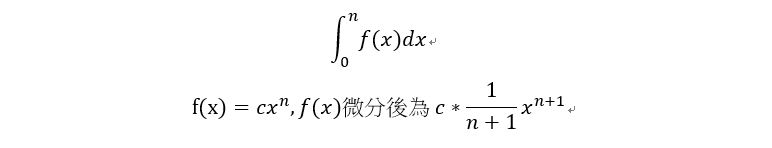

以下為簡單的例子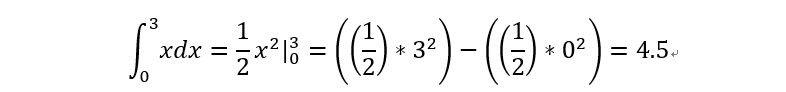

感謝您的瀏覽