前言

當神經網路含很多(Deep)神經層時，常會在其中放置一些 Batch Normalization 層，顧名思義，它應該是作特徵縮放，但是，內部是怎麼運作的? 有哪些好處? 運用的時機? 擺放的位置?

花了一些時間 google，將相關的資料整理如下，與同好分享，若有疏漏，請不吝指正。

作法

Sergey Ioffe 及 Christian Szegedy 在 2015 年首次提出 Batch Normalization 概念，論文的標題為【Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.】。

簡單的講，Batch Normalization 就是作特徵縮放，將前一層的Output標準化，再轉至下一層，標準化公式如下：
x_new = (x_old - μ)/ δ

標準化的好處就是讓收斂速度快一點，不作的話，通常先導向梯度較大的方向前進，造成收斂路線曲折前進，如下圖。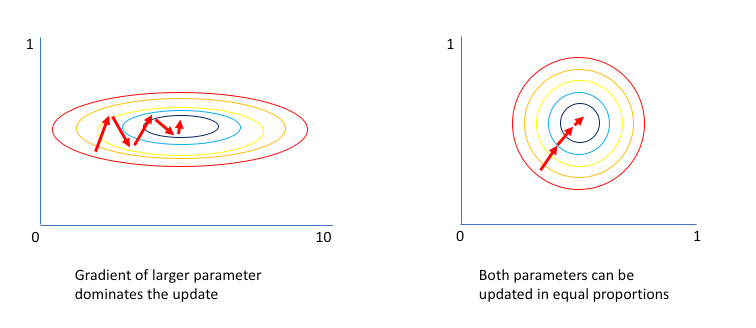

圖一. 不作標準化 vs. 作標準化 優化過程的示意圖，圖片來源：Why Batch Normalization Matters?

Batch Normalization 另外再引進兩個變數 -- γ(Gamma)、β，分別控制規模縮放(Scale)及偏移(Shift)。

圖二. Batch Normalization 公式，圖片來源：【Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.】

注意

1. 標準化訓練時逐批計算的。
2. γ、β值是由訓練過程中計算出來的，而不是事先設定的。

Internal Covariate Shift

假設我們訓練辨識狗的模型，訓練時我麼使用黃狗的圖片作訓練資料集，完成後，我們拿來辨識花狗，這時效果就不好了，必須拿全部資料再訓練一次，這種現象就稱為【Internal Covariate Shift】，正式的定義是【假設我們要使用X預測Y時，當X的分配隨著時間有所變化時，模型就逐漸失效了】。

像股價預測也是類似情形，當股價長期趨勢向上時，原來的模型就慢慢失準了，除非納入最新資料重新訓練模型。

以上情形利用 Batch Normalization 可以矯正此問題，因為每批資料都先被標準化，使input資料都屬於 N(0, 1)的Z分配。

Batch Normalization 優點

有些模型因為共享權值(Shared Weights)的關係，會使梯度逐漸消失或爆炸，如下：
若經過很多層
If W<1 ==> Wn --> 0 , 即梯度消失(gradient vanishing)
If W>1 ==> Wn --> ∞ , 梯度爆炸(gradient explosion)

每一次重新作標準化後，梯度重新計算就不會有以上問題。除此之外，Batch Normalization 還有以下優點：

• 收斂快(Train faster)。
• 使用較大的學習率(Use higher learning rates)。
• 權重初始化較容易(Parameter initialization is easier)。
• Activation function 在訓練過程中易消失或提早停止學習，經過 Batch Normalization 會再復活(Makes activation functions viable by regulating the inputs to them)。
• 全面準確率提升(Better results overall)。
• 有類似 Dropout 的效果，防止過度擬合(It adds noise which reduces overfitting with a regularization effect)，所以，用了 Batch Normalization，就少一點 Dropout，避免效果過強，反而造成低度擬合(Underfitting)。

詳細說明可參考原創【Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.】。

結論

有一篇文章【On The Perils of Batch Norm】 作了一個很有趣的實驗，他使用兩個資料集模擬『Internal Covariate Shift』現象，一個是MNIST資料集，背景是單純白色，另一個是SVHN資料集，有複雜的背景如下圖。

首先合併兩個資料集訓練一個模型，如下：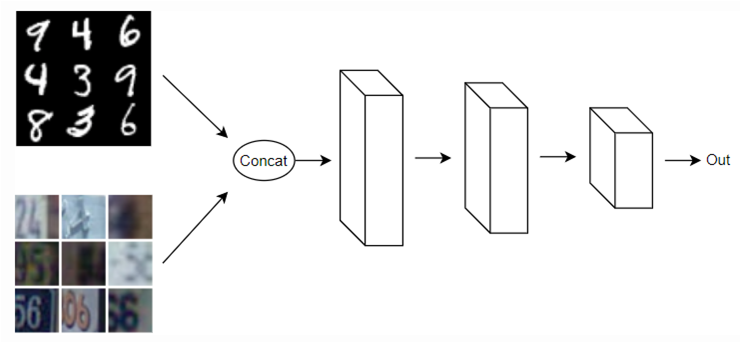

圖三. 合併兩個資料集訓練一個模型

2. 再使用兩個資料集個別訓練模型，但共享權值，如下：
   
   圖四. 使用兩個資料集個別訓練模型，但共享權值

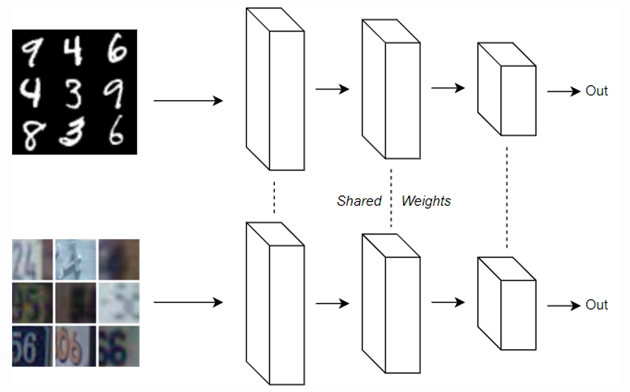
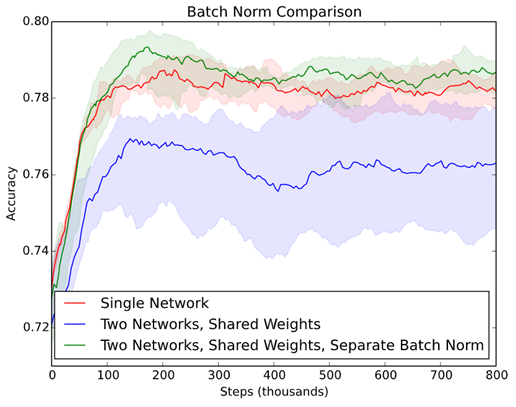
比較結果，兩者都插入Batch Normalization，前者，即單一模型準確度較高(紅線)，因為 Batch Normalization 可以矯正 【Internal Covariate Shift】現象。後者資料集內容不同，兩個模型共享權值就不對。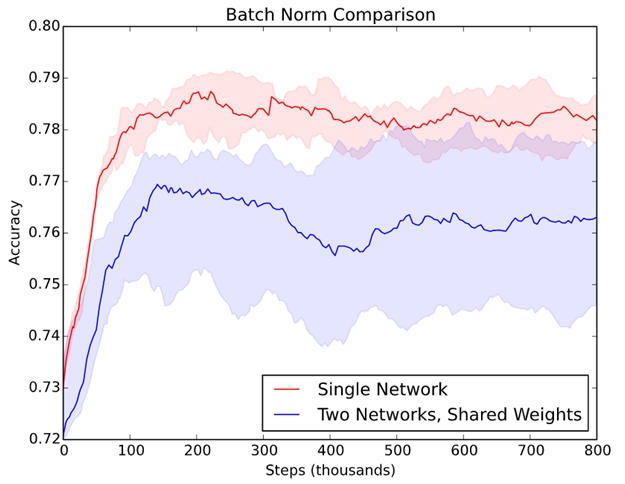

圖五. 兩種模型準確率比較

3. 再加上第三種模型：使用兩個資料集訓練兩個模型，個別作Batch Normalization，但不共享權值。比較結果，第三種模型效果最好。
   
   圖六. 三種模型準確率比較