前言

資料利用線性迴歸建構模型之後，因為每筆資料特性的不同，可能會有許多問題出現，今天的內容將提到幾個在線性迴歸模型建模後常見的問題。

常見的問題

1. 反應變數與解釋變數之間存在非線性關係(non-linearity relationship)
   線性迴歸模型將反應變數與解釋變數之間假設為線性關係，如果這樣的假設是對的，那麼表示利用這個迴歸模型的配飾值(fitted value)或預測值(predicted value)與殘差(residual, 配飾值減原始的觀察值)之間的關係應該不會存在明顯的模式，且要 均勻的散落在0的兩側才會是符合假設的情況 。換句話說，如果線性的模型假設已經足夠解釋這筆資料時，那麼剩下來不能由解釋變數解釋的部分，也就是殘差，就應該不會有其他訊息存在。例如下圖是常常用來檢查此假設的殘差圖(residual plot)，很明顯地看到殘差並沒有均勻地散落在0的兩側，而是有一個類似二次曲線的分佈，表示資料可能不滿足線性的假設，需要用其他更複雜的模型來建構，例如在模型中加入非線性的解釋變數轉換logX、X平方等等。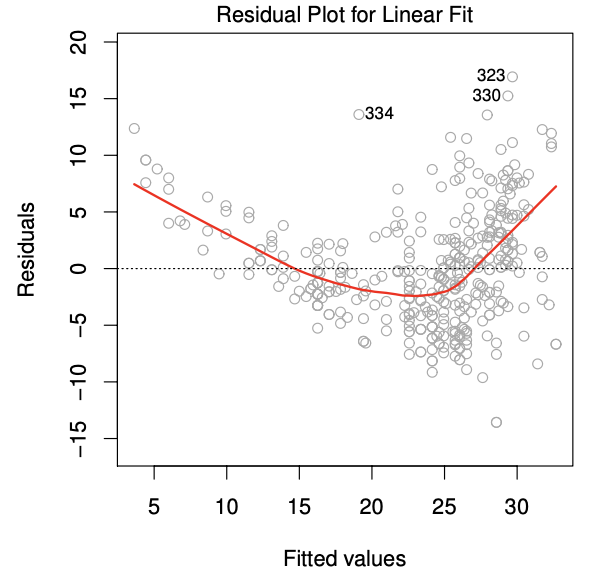
   

2. 誤差項的變異數不為一個常數(non-constant varaince)
   另一個在迴歸模型中的重要假設是：誤差項的變異數須為一個常數(constant variance)，，許多迴歸模型中的檢定方法都需要有這個重要的假設，例如迴歸係數的假設檢定(hypothesis test)、信賴區間(confidence interval)等。這個假設也可以由殘差圖來檢查，符合假設的圖形也應該要均勻的散落在0的兩側，例如下圖，隨著配適值越來越大殘差的分佈也越來越廣，表示殘差的變異數並非是一個常數違反了模型的假設，此時常見的處理方式是對反應變數做一些轉換來解決，例如利用log或開根號或許可以解決這樣的問題。
   

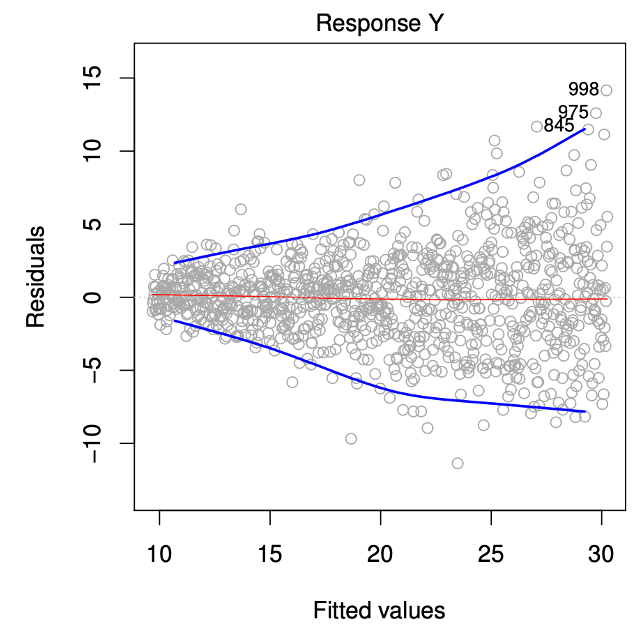
3. 離群值(outlier)
   離群值的定義是給定某解釋變數下，垂直距離迴歸直線異常遙遠的資料點(unusual response)。其成因有許多種，最常見的可能是有資料誤植的情況造成的，而離群值可能會造成模型的建構或估計參數出現問題，例如迴歸直線的截距與斜率，若沒有影響到前者也可能影響到殘差的標準差(Residual standard error, RSE)，造成預測模型的信賴區間、p-value與判定係數(R-square)受到影響，因此需要特別觀察資料是否有離群值存在，簡單線性迴歸可以畫出解釋變數與反應變數的散步圖與迴歸直線來檢查，多元迴歸模型可以使用殘差圖檢查較為方便，如下圖的紅點就為一個離群值。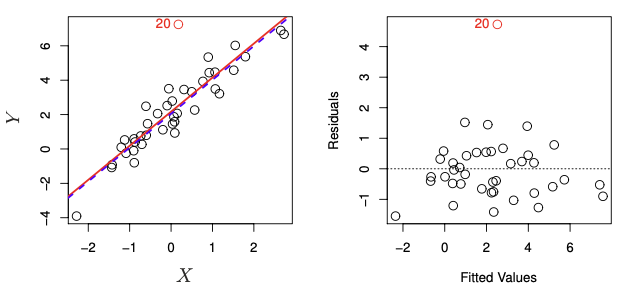
   

4. 高度槓桿點(high leverage points)
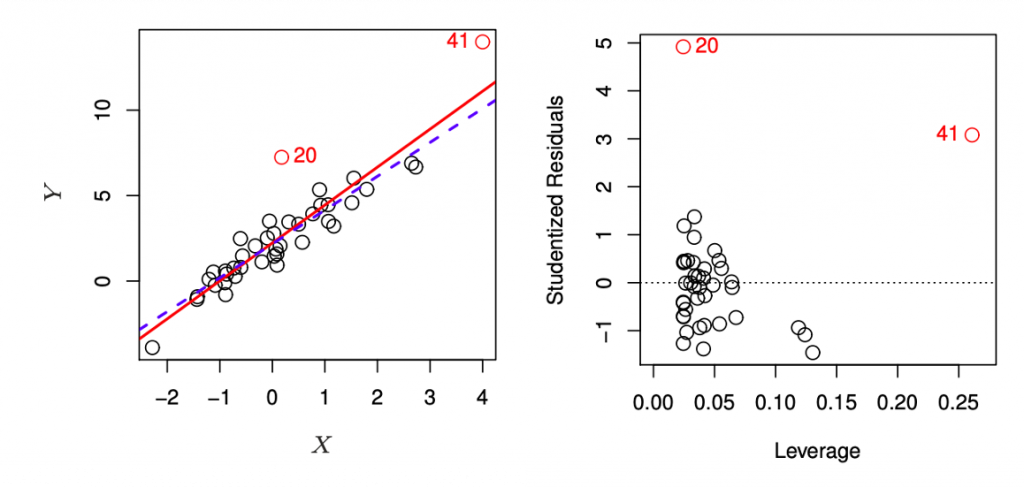
   上述提到離群值是垂直距離迴歸直線異常遙遠的資料點(unusual response)，而高度槓桿點指的是水平距離資料趨勢異常遙遠的資料點(unusual value for x)，這樣的資料點同樣會造成迴歸模型預測與估計的問題，例如下圖中，觀察點41就是一個高度槓桿點。而為了量化此數值，可以計算對應的統計量leverage statistic，若數值過大表示資料點x距離平均值很遠，有可能為一個高度槓桿點。

5. 共線性(collinearity)
共線性表示兩個或以上的解釋變數之間存在較高的相關性(correlation)，通常可以利用相關係數矩陣(correlation matrix)來初步的判定解釋變數之間是否相關性過高，具有較高的相關性時我們很難判斷各自對於反應變數直接的影響，並且可能會使估計迴歸係數的準確度降低，使其變異數變大估計較不穩定，甚至針對迴歸係數進行是否顯著的檢定時也會因為共線性產生問題。不過，並非所有共線性的問題都可以利用相關係數矩陣找出，即使沒有一對解釋變數之間具有高相關性，但並不代表三個或更多個之間的解釋變數之間也沒有高相關性，此問題稱為多重共線性(multicollinearity)問題。這時可以針對每個解釋變數計算variance inflation factor (VIF)來檢查，原理是輪流將要計算的解釋變數移除，並計算移除後模型的判定係數大小來決定。常見的解決方法有兩種，第一種是將具有高VIF數值的解釋變數移除；第二種是想辦法將具有共線性的幾個解釋變數合併為一個變數。

參考資料與圖片來源：
An Introduction to Statistical Learning