前言

在多元迴歸模型中，我們常常關心是否全部的解釋變數都可以幫助預測反應變數，或是只有部分的解釋變數有用？昨天的內容提到可以解決這類問題常見的方法有子集選取法(subset selection)、正規化(regularization)與降維(dimension reduction)等，今天將討論正規化或稱為收縮法(shrinkage methods)的方法來解決這類的問題。另外，使用這些方法除了找出重要的解釋變數外，在高維度，也就是資料維度p > 樣本數n時，以最小平方法求解迴歸係數的方法將會有問題產生。例如原來利用最小平方法估計的迴歸係數為 ，但若是在資料維度大於樣本數時(p > n)，則 將不存在反矩陣(inverse matrix)得迴歸係數無法順利求解，，因此需要進行變數挑選的幫忙減少模型中的迴歸係數來求解迴歸係數。且在機器學習的問題中，常常會有overfitting的狀況產生，也就是訓練出來的模型完全是訓練集資料的形狀，在訓練集表現得很好，而到了測試集的表現卻差了許多，而正規化迴歸模型也可以用來處理這類的問題。

正規化迴歸(Regularization regression)的方法是在原來迴歸模型中迴歸係數的求解過程加入一些懲罰項(penalty term)來限制迴歸係數數值的大小，將原來數值接近0的迴歸係數收縮到0，保留數值較大的迴歸係數(實際資料建構的迴歸模型，其迴歸係數很少真正等於0)，藉由這樣的方式達到變數挑選的結果。今日的內容會提到兩種不同加入懲罰項的正規化方法，分別是利用L2-norm的Ridge與利用L1-norm的Lasso。

Ridge

正規化迴歸模型的參數估計過程與最小平方法相似，只是加上了懲罰項來限制迴歸係數，不過都是利用使RSS(Residual Sum of Squares)最小的概念進行估計。在Ridge regression使用的是L2-norm來限制迴歸係數的數值，其中 稱為tuning parameter。當 時，懲罰項無法發揮效果，得到的結果與原來最小平方法相同；而當 時，懲罰項發揮最大的效果使迴歸係數都被收縮到0。因此tuning parameter的選擇將會影響到模型的參數估計，交叉驗證(cross-validation)常常被利用來選擇tuning parameter，在後續的內容將會提到如何利用交叉驗證來挑選參數或模型。

• Loss function:
• 
• 

一般來說，利用最小平方法的參數估計方法可以得到偏差(bias)較小但是變異(variance)較大的估計結果，也就是說在訓練集資料上有一些小小的變動可能就會造成估計上有很大的不同，Ridge regression可以在偏差與變異兩種考量下得到較穩定的估計結果，在高維度p > n的情形下也有優於最小平方法的表現。

Lasso

Ridge regression模型雖然經由懲罰項將迴歸係數的數值縮到接近0(無法真的將數值準確收縮到0)，但通常還是會包含所有的解釋變數。這樣的情形雖然不會對於預測的準確度造成問題，但是當解釋變數很多時模型解釋就會變得相對困難。Lasso regression可以解決這樣的問題，將不重要的解釋變數的迴歸係數數值縮到0，等同於在對資料進行變數挑選(variable selection)使模型變得容易解釋，因此近幾年比Ridge regression更受歡迎，Lasso使用的是L1-norm來限制迴歸係數的數值，其中tuning parameter也可以利用交叉驗證來挑選一個好的數值。

• Loss function:
• 
• 

圖解Ridge與Lasso

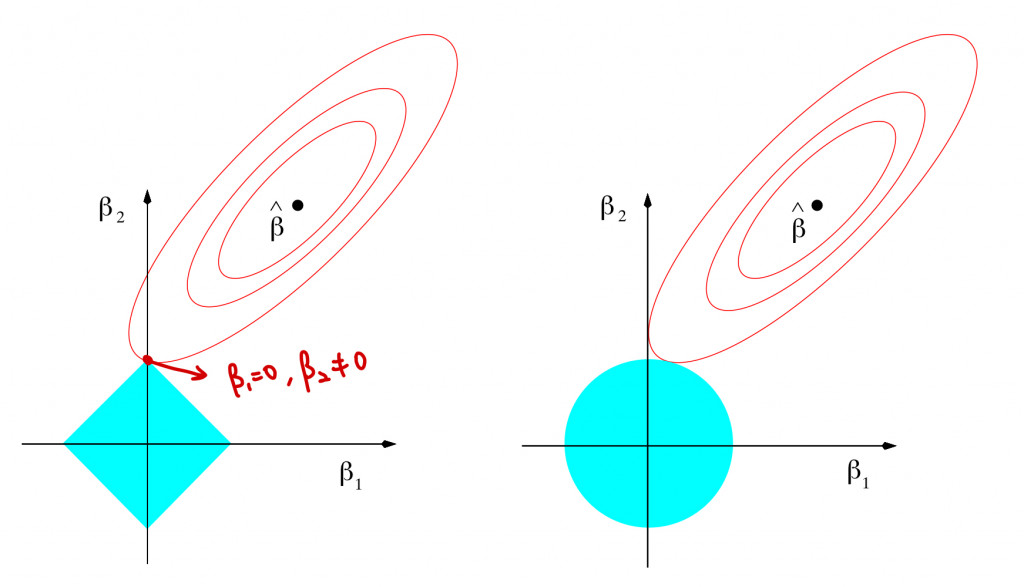
由上述定義Ridge與Lasso的loss function都可以拆解成兩部分，分別為原始最小平方法的RSS與懲罰項，上圖中紅色橢圓形為最小平方法針對迴歸係數的估計值，藍色區塊為正規化的懲罰項，兩者的交點就是正規化迴歸模型的參數估計結果，左圖描述的是Lasso的結果，右圖為Ridge。

Lasso使用的是L1-norm等同於限制迴歸係數數值加上絕對值後的總和，因此對應到藍色的菱形區塊。從圖中可以發現Lasso的懲罰項容易出現在兩軸上尖點，也因此會有迴歸係數數值為0的估計，例如上圖迴歸係數估計值為 與 。

Ridge使用的是L2-norm在限制迴歸係數數值的平方和，因此對應到藍色的圓形區塊。懲罰項呈現的圖形為圓形，沒有尖點，使得求解的估計值很難發生在軸上，也因此使用Ridge regression所估計出的迴歸係數數值很難真的為0。

雖然Lasso有可以挑選重要變數的功能，但對於模型的預測能力在不同資料結構下兩者互有高低，並沒有哪個方法一定比較好，不過兩者相較於子集選取法的運算上還是有明顯較好的效率！

參考資料與圖片來源：
An Introduction to Statistical Learning