前言

在機器學習中，常常把監督式學習根據反應變數是連續資料或類別資料，分為迴歸(Regression)與分類(Classification)兩大類，那麼如果利用線性迴歸模型(Linear regression)處理類別型的反應變數也就是分類問題時，會造成什麼問題以及為什麼線性迴歸方法不適合處理分類的問題？

建立迴歸模型

• 假設有一筆急診室患者的資料，希望由患者的症狀來預測可能的醫療狀況，分別為中風、藥物過量與癲癇發作。在線性迴歸的做法中，可以將這三種情形當成反應變數並且賦予數值，例如Y=1表示中風、Y=2為藥物過量與Y=3為癲癇發作，接著可以利用最小平方法針對反應變數與其他解釋變數建立線性迴歸模型。但在這個模型將類別型的反應變數賦予數值的方式，等同於假設中風和藥物過量之間的差異與藥物過量和癲癇發作之間的差異相同 ，但是在實際情況中我們並沒有辦法得知兩者的差異是否相等，或是利用其他數值來假設時也會有一樣的問題。也就是說在處理類別型變數的問題中，並沒有一個好的方法可以賦予量化的數值來建立迴歸模型。

• 若將上述的問題簡單化成兩種情形Y=0表示中風，Y=1表示藥物過量，建立線性迴歸模型，預測值Y若大於0.5表示預測為藥物過量，小於0.5則表示預測為中風。而剛好等於0.5時就會不知道要預測為哪一類，選擇其中一類時就好像偏袒了其中一類，因此這也是利用迴歸模型處理分類問題時會遇到的困難。此時的迴歸模型也等同於在估計機率P(藥物過量|X)。這樣的方法有個明顯的問題是預測的數值很可能大於1或小於0，且每類預測的機率總和常常會不等於1。如下圖：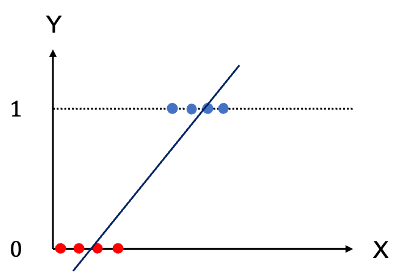
  

• 另外，還有一個線性迴歸模型常有的限制，也就是離群值(outlier)的影響，例如在上述Y只有兩類的情形中若存在一個資料點與大部分的資料差距較遠，那麼整個迴歸直線就很容易受到影響，產生與沒有outlier時的直線差距很大。如下圖：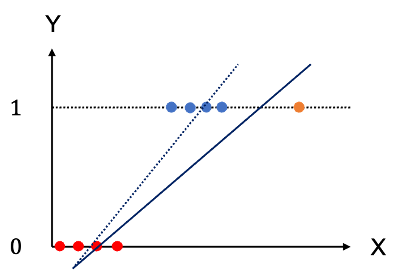
  

小結

由以上的幾個簡單的例子可以發現，若利用線性迴歸模型來處理分類的問題或預測類別型變數時，會產生幾個不太適合的現象，例如類別間的差異如何量化、將類別以數值表示時如何找到適合的閾值做切割、預測值為機率時的問題以及資料中有outlier的問題，以上的問題都顯示線性迴歸模型或許不是一個適合用來處理分類問題的方法，後續幾天的內容將包含常見的分類方法。