前言與介紹

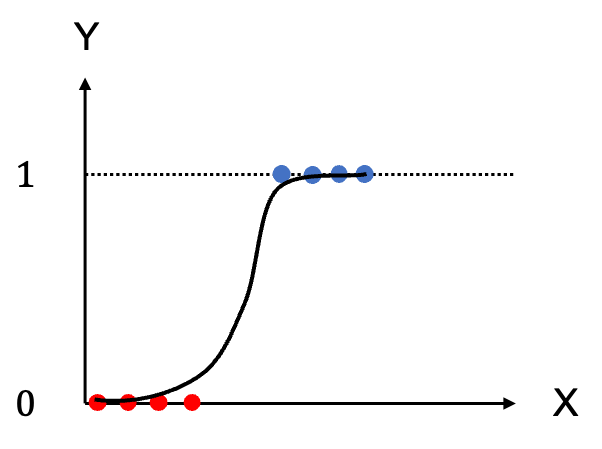
在機器學習中常常用來處理分類問題的方法之一為邏輯斯迴歸模型(Logistic regression)，與線性迴歸模型不同的是邏輯斯迴歸模型是直接針對類別型反應變數Y在給定解釋變數X下的機率，或稱為後驗機率(posterior probability)，將這個機率以解釋變數X的線性組合來建立迴歸模型。但若直接以X的線性組合建立與機率的迴歸模型就會出現以線性迴歸一樣的問題，因此在邏輯斯迴歸中將機率做logit轉換，也就是將勝算(odds)取log，也稱為log odds，轉換後的log odds作為反應變數後建立線性迴歸模型，因為轉換過後的反應變數已經不是0~1之間的數，而是可以從負無限大到無限大的數值，就解決了以線性迴歸模型會造成的問題。如下式為只有一個解釋變數的邏輯斯迴歸模型，也就是將反應變數當成log(odds)的簡單線性迴歸模型，此時的模型雖然與簡單線性迴歸模型相似，但迴歸係數的解釋已經不同，而經過一些數學轉換後可以得到每一個類別預測的機率，並且可以確保每類的總和為1。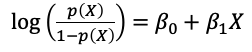

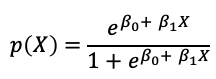
• 估計完參數後，轉換回機率y=P(X)所繪製的迴歸線如下圖所示，解決了線性迴歸模型中遇到的問題，例如預測值大於1或小於0，且對於outlier的影響也相對減少了。
  

建立多元邏輯斯迴歸模型(multiple logistic regression)

• 假設有K個類別，多個解釋變數x的資料，將第K類當成比較的組別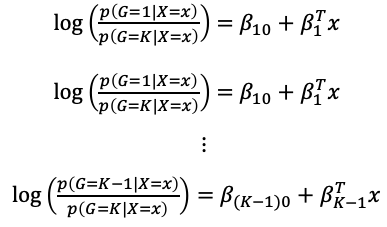
  

• 每一類的機率經過轉換後可以寫成以下的形式，每個類別加起來的總和為1: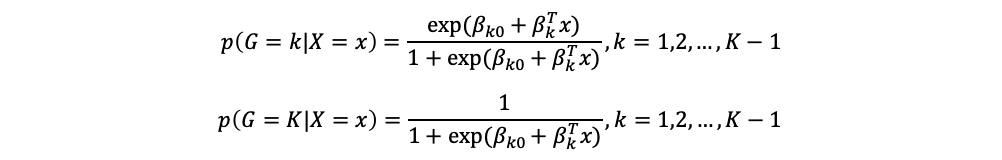
  

• 假設只有反應變數只有兩類Y={0,1}，且服從伯努利分布(Bernoulli distribution)，試著以最大概似估計法(Maximum likelihood estimation, MLE)求解參數(邏輯斯迴歸模型為非線性模型，因此不適合使用最小平方法求解)：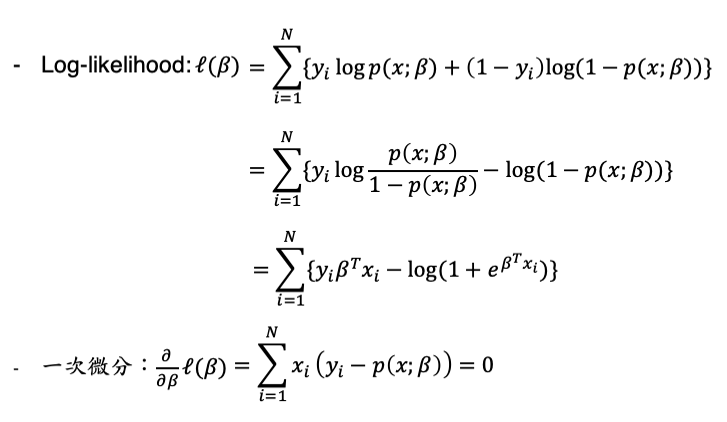
  

• 一次微分後的log-likelihood對於為非線性組合，且夾在exponential函數中無法利用上述微分後的式子找到迴歸係數的closed-form，因此需要利用牛頓法迭代才能求得。

• 牛頓法(Newton-Raphson algorithm)，要求解的對象為一次微分後的式子，首先需要將二次微分的函數求出，接著以一個初始值開始進行迭代。
  
  

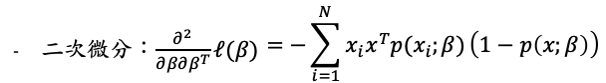
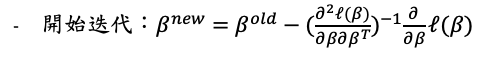
• 接著若把一次微分與二次微分寫成矩陣的形式：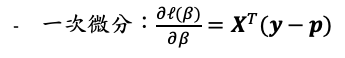
  
  

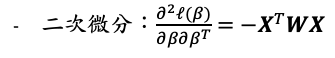
• 代入牛頓法的式子：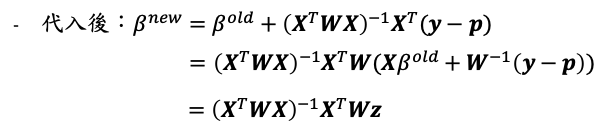
  

• 其中稱為調整後的反應變數(adjusted response)。若當成反應變數時，此次迭代迴歸係數的解就與最小平方法的結果相似只是多了一個W的權重，因此稱為迭代加權最小平方法(literatively reweighted least squares estimation, IRLS)。因此要求解的新迴歸係數為：
  

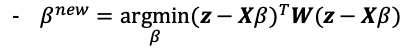
• 以牛頓法迭代的方式重複執行直到收斂就可以求得迴歸係數的估計值

邏輯斯迴歸模型與線性迴歸模型處理分類問題的比較

兩者處理分類問題時都是針對反應變數給定解釋變數的機率建構模型，但線性迴歸模型是假設此機率與解釋變數X為線性關係，因此最後的估計值極有可能大於1或小於0，且不能確保每一類的機率總和為1。然而，邏輯斯迴歸模型是將此機率以X非線性函數的方法使機率的數值可以介於0到1之間，或者說邏輯斯迴歸模型是將此機率藉由logit轉換後，再以X的線性函數建立模型。

參考資料

The Elements of Statistical Learning