前言

接下來幾天要開始講一些比較複雜、沒那麼直觀的機器學習模型。首先會大致講解一下原理，後面再附上基礎的一些程式碼示範。今天就來講講支援向量機( SVM, Support Vector Machine )。

[分類]支援向量機( SVM, Support Vector Machine )

• 支援向量機 SVM
• 參數討論
  • 參數調整(Tuning Parameters)
• SVM 優缺點
• [ R, Python Code] 基礎 SVM 模型

支援向量機 SVM

SVM是一種二元分類器(Binary Classifier)，是一種基於統計學習理論的監督式學習的分類演算法，由俄羅斯的統計學家 Vapnik 等人所提出。

簡單地說，SVM 會試圖從資料中建構一個超平面，將資料區分成兩個類別，最後再進行預測或分類。

[註- 超平面(Hyperplane):]
在二維的空間中，超平面指的就是「一條線」，三維空間中，則是「一個平面」。
之所以有一個「超」字，是因為資料往往不會只有二維、三維。在更高維的空間中，我們無法觀察這個平面的形狀為何，於是就用「超平面(Hyperplane)」一詞來概括。

SVM 支援向量機如今常常被應用在各種領域、問題，包含:

• 小數據的運用(準確率高，且和深度學習不同，不需要大數據在背後支援)
• 非線性可分(non-linear separability)的問題
• 高維模式識別問題上 (醫學、圖像辨識分類等等)

SVM 延伸:

1. 多元分類: 當我們想分類的資料不只有兩種類別時， SVM 仍然可以幫忙我們解決，這時候就要結合 OVA、OVO的策略處理多元分類問題。
2. 迴歸問題: 在處理迴歸問題、想對連續資料的進行預測時，可以使用 SVM 的延伸型態 SVR ( Support Vector Regression )。

以上兩個延伸會在明天做介紹並補充程式碼。

支援向量機 SVM 概念

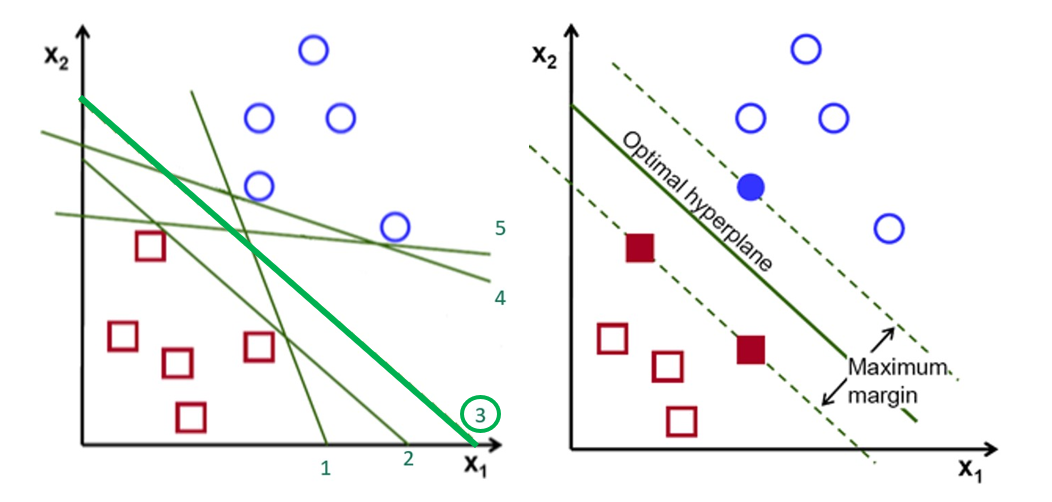
示意圖這邊以二維(X1, X2)的空間上分類舉例:
SVM在找一個 Optimal hyperplane ，希望區隔兩類之間的邊界(Margin)可以越寬越好。
這個 margin 的邊界附近的點會協助計算建立這個 hyperplane，這些點就是所謂的支持向量（Support Vector），引此這個分類方法被稱為「支援向量機」( Support Vector Machine )。

左圖來說，雖然線1-5都能將資料分成兩類，但是3號線分類的邊界最寬，整體距離其他的資料點比較遠，因此由這些資料點支援，我們訓練出了最適當的分類超平面線3號。

如果是多維的資料，SVM 就會將資料投影到更高的維度，然後建構一個超平面(Hyperplane)，讓資料在高維空間中能夠被分割: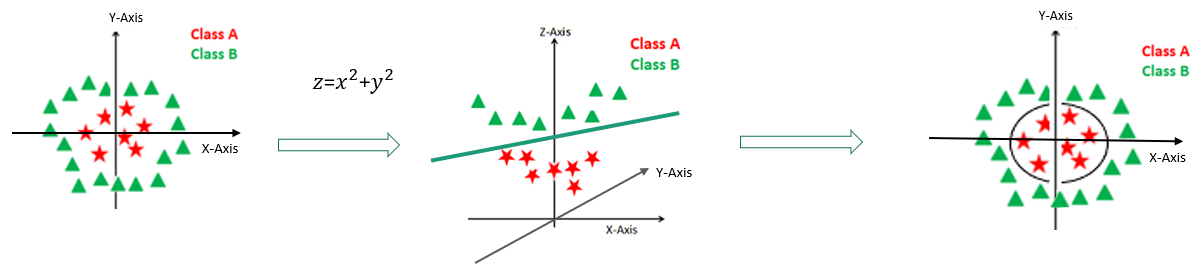

這邊是在多維資料點上使用Polynomial kernel分類兩種資料的示意影片(@udiprod):
SVM with polynomial kernel visualization

參數討論

• kernel  = 將資料映射到特徵空間的核函數，用來處理「非線性可分」 的問題。
  搭配到好的kernel 函數能讓SVM在分類問題中得到非常好的效能。

當我們無法在原始空間(維度)中適當的找到一個線性分類器將兩類區隔開，這時後此需要找到一個非線性投影將資料進行轉換到更高維度的空間，讓我們在高維度的空間中只需要一個線性分類器/Hyperplane就可以完美分類。因此我們需要 kernel函數 來輔助設計一個好的非線性投影公式。

參數調整(Tuning Parameters)

• cost = 決定給被誤差/分錯的資料「多少」懲罰值。

• gamma = 在kernel-function裡面的參數，決定資料點的影響力範圍。

• epsilon = margin of tolerance。越大，表示在容忍範圍內的誤差/分錯的資料，不會被懲罰；反之，越接近0，每一個誤差/分錯的資料都會被懲罰。

• 什麼參數設定下 SVM/SVR 容易 Overfitting ?

在調參數的階段，通常會使用 grid search 的手法。概念是針對每一種參數組合，都會訓練一個對應的模型，最後觀察模型的表現，挑出表現最佳的模型。

在訓練的過程中，R 裡e1071套件內建tune()的函式，可以幫助我們調整參數，它會自動引入cross validation的手法，確保模型的可靠度(Robustness)，讓tune出來的參數是可以採用的。

SVM 優缺點

• 優點

1. 在高維空間下仍然有效，可以處理高維數據
2. 過不同核函數的選擇，可以處理不同的資料
3. 內存等資源開銷小

• 缺點

1. 效能不佳(耗時)
2. 方法本身無法直接估計機率 (可以用K-Fold CV的方法計算機率，但是耗時)
3. 如果特徵數目過分多於樣本數目，效果則會有所下降

[R][PYTHON] 基礎 SVM 模型

[R Code] SVM 基礎模型

要建立 SVM 模型時會使用到e1071套件中的svm( )函式。

install.packages("e1071")
library(e1071)

svm(type = ‘C-classification’,  # ‘C-classification’(SVM 類別Y)/’eps-regression’(SVR 連續Y)。 
    kernel =‘radial’, # 將資料映射到特徵空間的 kernel-function，可用來處理「非線性可分」的問題。 
	## 以下為參數調整:
    cost =  C, # 在Lagrange formulation中的大C，決定給被誤差/分錯的資料「多少」懲罰值。 
    gamma =  g, #在kernel-function裡面的參數(linear-function除外)。
    epsilon = e #margin of tolerance。越大，表示在容忍範圍內的誤差/分錯的資料，不會被懲罰；反之，越接近0，每一個誤差/分錯的資料都會被懲罰。   
  ) 

其他 kernel function: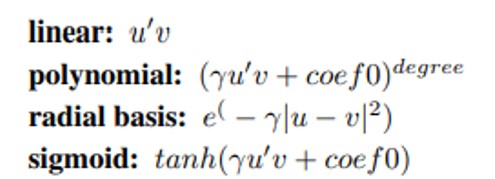
[補充]使用台大林智仁教授所開發的libsvm，在R中對應的套件是e1071，詳細說明可以參考以下網址:
https://www.csie.ntu.edu.tw/~cjlin/libsvm/
https://cran.r-project.org/web/packages/e1071/e1071.pdf

[Python code] SVM 基礎模型

建立 SVM 的分類模型時，會使用到sklearn.svm套件中的svm.SVC( )函式。

#Import svm model
from sklearn import svm

#Create a svm Classifier model
clf = svm.SVC(kernel='linear') # Linear Kernel

#Train the model using the training sets
clf.fit(X_train, y_train)

#Predict the response for test dataset
y_pred = clf.predict(X_test)

#from sklearn import metrics

# Model Accuracy: how often is the classifier correct?
from sklearn import metrics
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

那多元分類的SVM( OVA、OVO ) 和 SVR 說明就等到明天了~

參考資料、網站

SVM with polynomial kernel visualization (HD)(@udiprod)
https://www.udiprod.com/about/
https://youtu.be/OdlNM96sHio
Support Vector Machines with Scikit-learn Tutorial(@Avinash Navlani)
https://www.datacamp.com/tutorial/svm-classification-scikit-learn-python