於第二十篇中，我們有提到Silhouette(輪廓)，它是一個評估群聚效果的方法，可以幫我們找尋到最佳群聚數。而今天我們就來深入了解其含意，並且利用它來找出數據中的離群點，那我們開始著手吧!

視覺化理解Silhouette

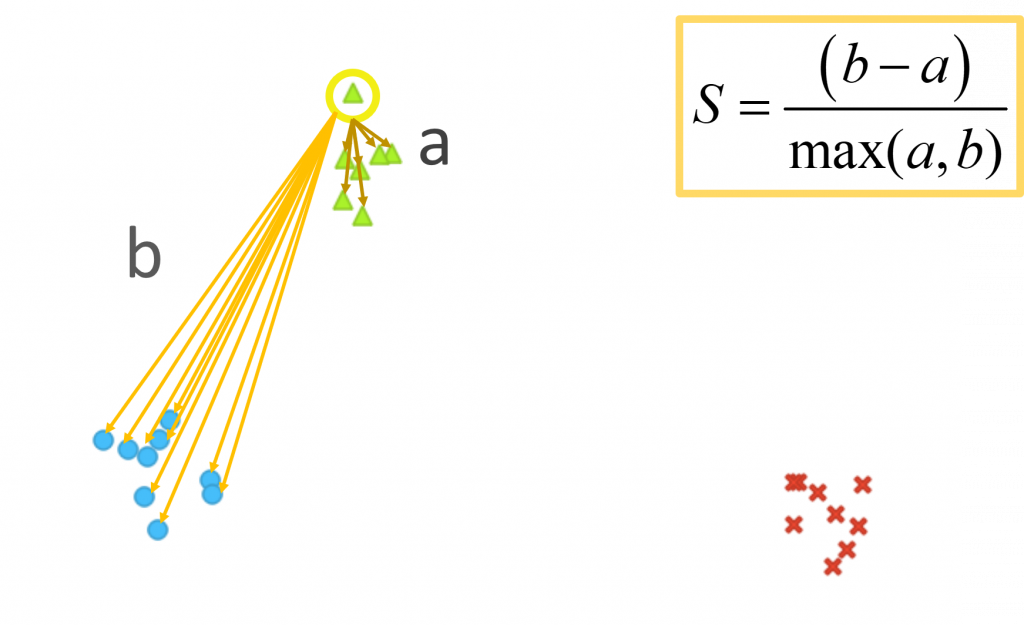
在上次第二十篇補充說明時，有說道我們令a為「同組之間的距離」代表，而b為「不同組間的距離」代表，從下面的圖來看，被黃色圓圈圈起的綠色點歸屬於綠色的族群，所以按理來說b會比a還要大，我們將他們相減，再經過標準化(也就是除以max(a,b))，得出來的結果就是「Silhouette Coefficiency(輪廓係數)」。

從以下範例來說，這個數據點的S值會很大，因為它非常偏向自己的群中，若有一值於兩群間，那麼它的S值會趨近於0。

手繪數據點

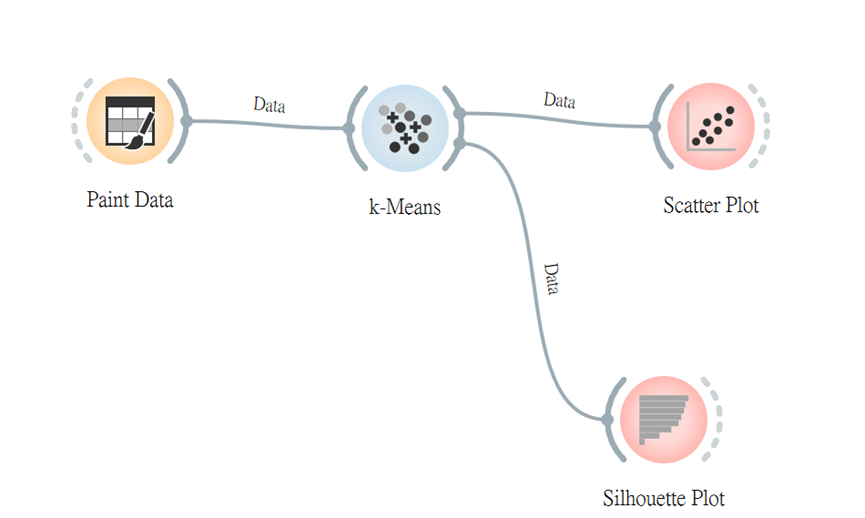
上面的圖片是我利用「Paint Data」繪製數據點，連接「k-Means」設定k=3(三個族群)，接著應用「Scatter Plot」視覺化數據點。

利用Silhouette找出質心點

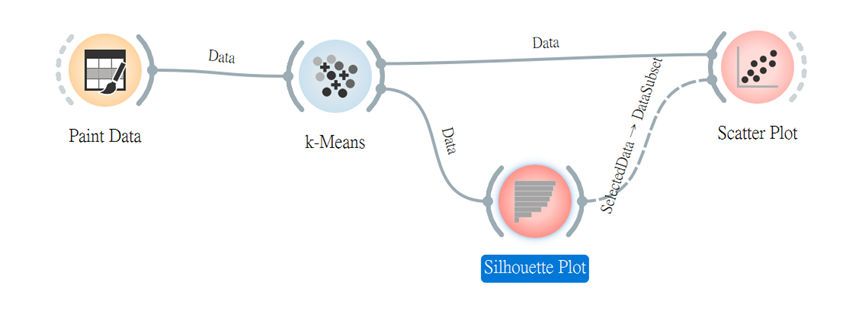
再來由「k-Means」外接「Silhouette Plot」，並將其連接「Scatter Plot」，找出離數據群中最接近的數據點。

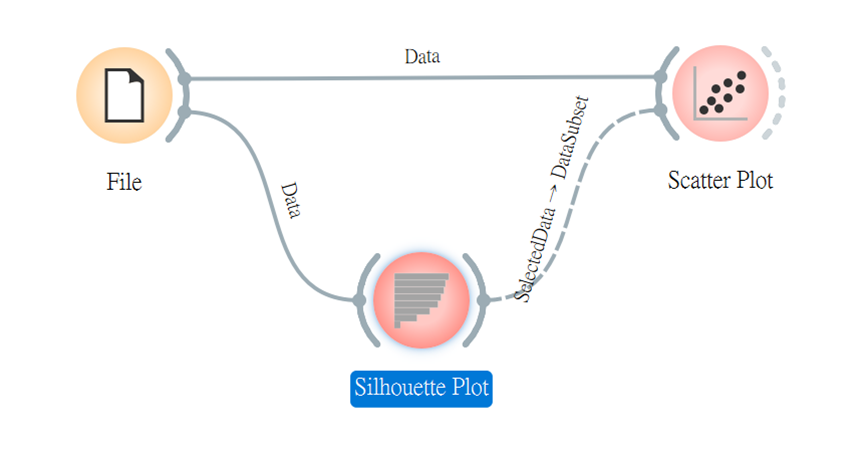
接著可以將Silhouette Plot與Scatter Plot放兩邊對照觀察，S值低者，皆在數據群中的邊界處；反之亦然。

真實數據呈現

此用法不限於離散或連續型數據，我們可以利用鳶尾花數據看看成效。

看完後，大家是否都知道如何找尋數據集中的離群點了呢~
那麼今日就先到這囉，掰掰~

參考資料:
Orange
Kmeans分群演算法 與 Silhouette 輪廓分析