前言

昨天介紹了簡單線性迴歸模型的基本架構，當資料只有一個解釋變數或特徵時(一個反應變數Y，多個解釋變數Ｘ的情境)，這個方法相當方便且容易解釋，但是當資料存在較多解釋變數的情況或許就沒那麼適合繼續使用簡單線性迴歸模型。雖然還是可以繼續利用該模型分別針對每個解釋變數建模，不過這樣的做法存在幾個問題，例如只有一個反應變數時，要如何整合這幾個簡單線性迴歸模型並進行預測；分別建構的模型都忽略了其他解釋變數的影響。因此一個比較合適的方法是將簡單線性迴歸模型延伸到多元線性迴歸模型(Multiple Linear Regression)，使迴歸模型可以同時放入多個解釋變數來進行預測以及估計，今天的內容練習以矩陣的方式呈現，並且加上幾何的角度來看看線性迴歸模型。

多元線性迴歸模型(Multiple Linear Regression)：

多元線性迴歸模型為利用多個解釋變數X預測反應變數Y，與簡單線性迴歸相似，但認為加入其他解釋變數可能可以改善模型的表現，因此在模型中納入更多解釋變數來說明或預測反應變數。其中Y為連續型的變數，每個X可以是連續或類別的變數，模型中Y沒有辦法以這些X解釋的部分也會落在誤差項(error term)，以下是模型架構(假設有p個解釋變數x，為p維的向量)：

• 資料： ,

• 模型： 或

• 參數： ,

• 模型假設：(與簡單線性迴歸模型一致)

  1. 解釋變數X與反應變數Y之間的關係為直線的(linear)
  2. 樣本之間互相獨立(independent)
  3. Y在X的任一個數值下都服從常態分佈，且變異數為一個常數

參數估計(最小平方法)：

在多元迴歸模型求解參數的方法與簡單線性迴歸類似，今天的內容以矩陣來表示：

• 殘差的平方和(RSS)：
•   and  
•   ⇒  

以幾何的角度解釋迴歸模型：

從昨天或今天提到的迴歸模型中可以發現，這個模型想將反應變數Y寫成解釋變數X的某種線性組合，換句話說就是想找到最能夠描述Y的那一種X的線性組合，或是說以X的角度來描述Y。因此可以想成空間投影的概念，將反應變數Y投影到X構成的空間中，如下圖：

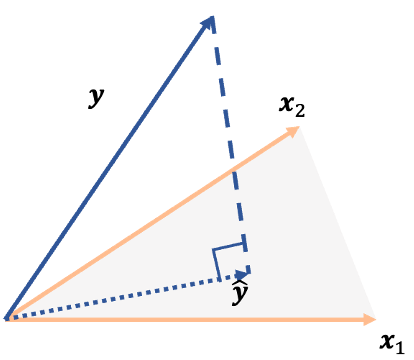
• 上圖的估計值可以寫成

• 由上述定義的反應變數估計為
  可以將上式想成將反應變數y投影到x空間的方法，因此也被稱為投影矩陣(projection matrix)或hat matrix

幾個多元線性迴歸模型的重要問題：

1. 是否至少有一個解釋變數對於預測反應變數是有用的？
   Ans: 可以利用假設檢定(hypothesis test)來檢查各個解釋變數的效果。
2. 是否全部的解釋變數都可以幫助預測反應變數，或是只有部分的解釋變數有用？
   Ans: 經由上個問題中挑選出幾個會影響反應變數的解釋變數後，下個問題是哪幾個變數更為重要，也就是變數挑選 (variable selection)的問題(在高維度資料中也會面臨變數挑選的問題，正規化的內容中會提到)。最直覺的做法是將所有解釋變數組合情形都拿去與反應變數建立迴歸模型後，再利用一些指標來選擇，例如Mallow's Cp、Akaike information criterion(AIC)、Bayesian information criterion(BIC)與adjusted R square等等。不過如果想要將每種可能都配飾一遍，就需要嘗試 種可能的模型，因此有兩大類常見的挑選變數方法，子集選取法(subset selection)、正規化(regularization)與降維(dimension reduction)的方法。子集選取法包含：向前選取法(forward selection)、向後刪除法(backward selction)與逐步迴歸法(stepwise selection)，細節不在此系列文章討論，簡介如下；正規化與降維的方法將會在後面的內容中提到。
   • 向前選取法(forward selection)：從沒有解釋變數的空模型(null model)開始，逐一加入解釋變數，直到滿足某個指標為止(例如AIC或BIC等)。
   • 向後刪除法(backward selection)：從一個完整包含所有解釋變數的模型開始，逐一刪除當下最不顯著的變數，直到達成某個指標為止。
   • 逐步迴歸法(stepwise regression)：結合以上兩種方法，由null model開始像向前選擇法一樣逐一添加變數，而隨著新的變數加入模型後，某個模型中的變數若p-value上升到某個閾值時，就刪除該變數。持續執行這樣的方法直到模型中的變數都是顯著的變數，且模型外的變數加入後都會使模型中原來的變數不顯著的情形。缺點是運算速率就會變慢。
3. 模型建構後，如何評估模型的好壞與準確率？
   Ans: 在簡單線性迴歸模型或多元線性迴歸模型中，最常用來衡量模型的方法是判定係數(Coefficient of determination)，代表反應變數Y的變異中可以被解釋變數X所解釋的比例，判定係數愈接近1表示此模型可以解釋大部分反應變數的變異。其他指標還有例如：殘差的標準差(Residual standard error, RSE)、均方根誤差 (Root mean square error, RMSE)、平均絕對誤差 (Mean absolute error, MAE)與均方根誤差 (Root mean square error, RMSE)等，以上的指標都可以藉由將資料切割為訓練集與測試集，接著計算得到。